归并排序

 

首先归并排序使用了二分法，归根到底的思想还是分而治之。拿到一个长数组，将其不停的分为左边和右边两份，然后以此递归分下去。然后再将她们按照两个有序数组的样子合并起来。

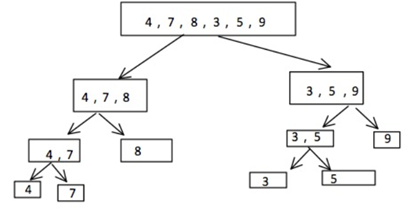
这里显示了归并排序的第一步，将数组按照middle进行递归拆分，最后分到最细之后再将其使用对两个有序数组进行排序的方法对其进行排序。

两个有序数组排序的方法则非常简单，同时对两个数组的第一个位置进行比大小，将小的放入一个空数组，然后被放入空数组的那个位置的指针往后 移一个，然后继续和另外一个数组的上一个位置进行比较，以此类推。到最后任何一个数组先出栈完，就将另外i一个数组里的所有元素追加到新数组后面。

由于递归拆分的时间复杂度是logN 然而，进行两个有序数组排序的方法复杂度是N该算法的时间复杂度是N*logN 所以是NlogN。

根据这波分析，我们可以看看对上图的一个行为。

当最左边的分到最细之后无法再划分左右然后开始进行合并。

第一次组合完成[4, 7]的合并

第二次组合完成[4, 7, 8]的合并

第三次组合完成[3, 5]的合并

第四次组合完成[3, 5, 9]的合并

第五次组合完成[3, 4, 5, 7, 8, 9]的合并结束排序。

归并排序的实现：

def merge_sort(alist):

       n =len(alist)

       if n <= 1:

              return alist

       mid = n//2

       #left采用归并排序后形成的有序的新的序列

       left_li = merge_sort(alist[:mid])

       #right采用归并排序后形成的有序的新的序列

       right_li = merge_sort(alist[mid:])

       #将两个有序的子序列合并为一个新的序列

       #merge(left, right)

       left_pointer, right_pointer = 0, 0

       result = []

      

       while left_pointer < len(left_li) and right_pointer < len(right_li):

              if left_li[left_pointer < right_li[right_pointer:]

                     result.append(left_li[left_pointer])

                     left_pointer += 1

              else:

                     result.append(right_li[right_pointer])

                     right_pointer += 1

              result += left_li[left_pointer: ]

              result += right_li[right_pointer: ]

              return result