贪心算法与动态规划

接下来学习贪心算法和动态规划，学习的过程中由于看的是录播，发现老师上课发现人有些没来有些许失落，下次在没有确定有充足时间的情况下，取消一切网络课程的报名。

贪心算法

贪心算法在求解某个问题时，总是做出眼前的最大利益，也就是说只顾眼前不顾大局，所以他是局部最优解。
贪心算法不是对所有问题都能得到整体最好的解决办法，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的状态不会影响以后的状态，只与当前状态有关。

贪心算法两个重要的特点是：
（1）贪心策略
（2）通过局部最优解能够得到全局最优解

会议安排问题

有N个同等级的会议需要在同一天使用同一个会议室，现在给出这N个会议的开始时间和结束时间，怎么样才能使会议室最大利用，安排最多场次的会议？

分析：这个问题需要用到贪心算法，即先将这些会议根据结束时间自然排序，肯定是先安排最先结束的，如果最先安排最后结束的，那如果一个会议开的很久，那本来可以多安排几场结果全被这个占了，显然不是最优的选择，因此优先安排会议先结束的才是合理的。然后接着在剩余的场次里判断会议开始时间是否在当前会议结束时间之后，如果在后面说明可以继续安排，下面就是代码实现。

（1）定义会议实体类，需要实现Comparable接口。

/**
 * 会议类，需实现Comparable接口
 */
public class Meeting implements Comparable<Meeting>{
    //定义会议属性
    private int number;
    private int starTime;
    private int endTime;

    //get set方法
    public int getNumber() {
        return number;
    }

    public void setNumber(int number) {
        this.number = number;
    }

    public int getStarTime() {
        return starTime;
    }

    public void setStarTime(int starTime) {
        this.starTime = starTime;
    }

    public int getEndTime() {
        return endTime;
    }

    public void setEndTime(int endTime) {
        this.endTime = endTime;
    }

    //构造方法
    public Meeting(int number, int starTime, int endTime) {
        this.number = number;
        this.starTime = starTime;
        this.endTime = endTime;
    }

    @Override
    public String toString() {
        return "Meeting{" +
                "number=" + number +
                ", starTime=" + starTime +
                ", endTime=" + endTime +
                '}';
    }
    //需要重写接口的方法
    @Override
    public int compareTo(Meeting o) {
        //按照会议结束时间升序排列
        if(this.endTime>o.endTime){
            return 1;
        }
        if(this.endTime<o.endTime){
            return -1;
        }
        return 0;
    }
}

（2）测试类，里面实现动态规划算法。

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;

/**
 * 贪心算法，用来解决会议安排问题
 */
public class Greedy {

    public static void main(String[] args) {
        //得到会议信息
        Scanner scan=new Scanner(System.in);
        System.out.println("请输入会议数量");
        int count=scan.nextInt();
        List<Meeting> list=new ArrayList<Meeting>();
        for (int i = 0; i < count; i++) {
            int starTime=scan.nextInt();
            int endTime=scan.nextInt();
            Meeting m=new Meeting(i,starTime,endTime);
            list.add(m);
        }
        System.out.println("会议信息");
        for (Meeting meeting : list) {
            System.out.println(meeting);
        }
        //贪心策略：按照会议结束时间排序，优先安排最先结束的
        //然后接下来从后面的会议里，寻找会议开始时间在当前会议结束时间之后的
        Collections.sort(list);
        int currentMeetingEndTime=0;
        System.out.println("贪心算法后会议安排");
        for (int i = 0; i <count; i++) {
            //判断会议结束时间
            Meeting m=list.get(i);
            if(m.getStarTime()>=currentMeetingEndTime){
                System.out.println(m);
                //更新当前会议结束时间
                currentMeetingEndTime=m.getEndTime();
            }
        }
    }
}

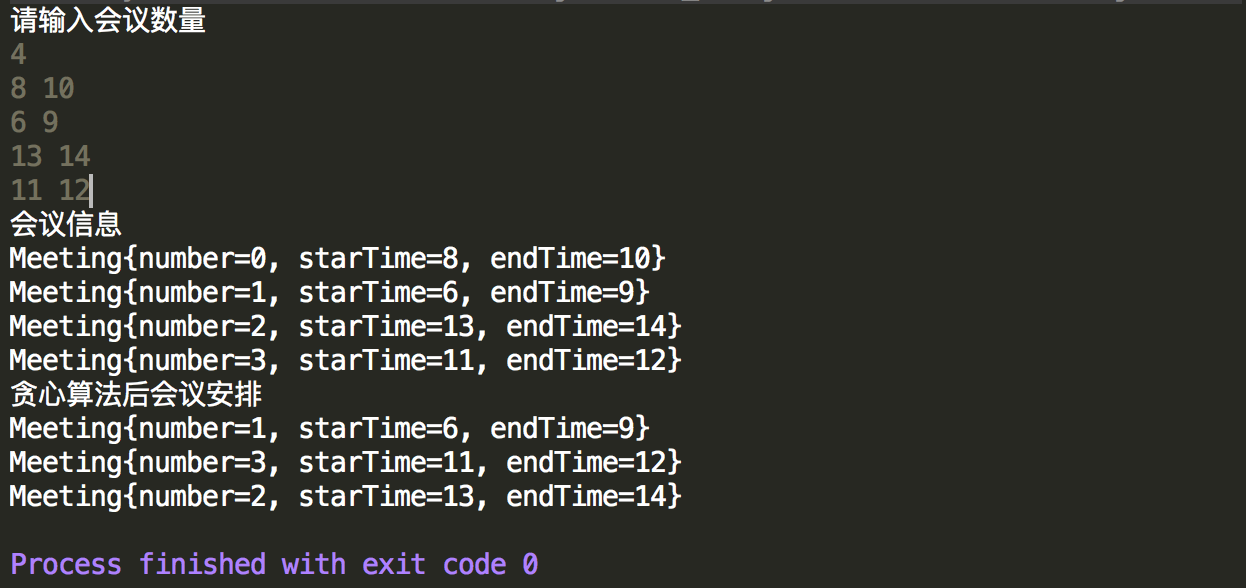
控制台输出结果，输入会议后，先按照会议结束时间自然排序，因此首先安排6点-9点场，然后应该是8点-10点场，发现会议开始时间在上一场结束时间之前，因此不安排。继续判断下一场11点-12点场，发现其会议开始时间在上一场之后，因此安排，最后一场同理，因此结果是OK的。

动态规划

动态规划核心思想：分解子问题，通过局部最大值得到全局最大，需要用到表格的分析。

背包问题

小偷去商店盗窃，背里有一个包，容量是50kg，现在有如下的物品（物品不能拆分，数量均为1），请问小偷应该怎么样拿才能得到最大的价值？

物品1 重量10kg 价值60元

物品2 重量20kg 价值100元

物品3 重量40kg，价值120元

分析：这个问题需要使用动态规划，先将上述问题缩小10倍，可以将背包进行拆分，当背包从1kg到5kg，然后物品从第一个到第三个，看能放的最大价值。

（1）放入第一个物品：背包为1kg时，可以放进去，价值最大就6元，当背包容量达到2以后，依然只有一个物品可以放，因此能得到的最大价值都是6元。

（2）放入第二个物品：背包为1kg时，虽然有第二个物品的选择，但是依然只能放进去第一个物品，因此最大价值依然是6，当背包容量达到2kg时，这个时候有小偷有两种选择，选择不放入第二个物品，这样它依然是6元，选择放入第二个物品，拿出第一个物品，这样价值变成10元，比较后选择后者，因此最大价值就是10元。当背包达到3kg时，一样判断，他可以选择放第一个物品，还有放第二个物品+第一个物品，所以变成16，以后按照此推均为16元。

（3）放入第三个物品：跟前面一样，当背包容量没达到4kg时，小偷只能选择上一个背包重量下最佳选择。当背包达到4kg时，他又有两种选择，选择上一次最佳选择16元，或者丢弃上一次最佳选择，换成装进去一个4kg的物品，这样价值为12元，比较后还是选择前者，因此4kg下最优就是16。当背包达到5kg时，就会比较16和18，最终选择18。

以下是代码实现。

/**
 * 背包问题，使用动态规划，即分解子问题，通过局部最大值，逐渐得到全局最大值
 */
public class DP {

    public static void main(String[] args) {
        //物品重量和价值，一一对应
        int[] weight=new int[]{10,20,40};
        int[] value=new int[]{60,100,120};
        //背包容量50kg
        int capacity=50;
        //物品个数 3个
        int count=3;
        //根据表格分析，创建二维数组
        int[][] packageValue=new int[count+1][capacity+1];

        //动态规划分析，判断每个格子的最大值
        for (int i = 1; i <=count; i++) {//外层循环代表放第几个物品
            for (int j = 1; j <= capacity; j++) {//内层循环代表背包重量逐渐增加
                //根据上述表格的分析，得到如下逻辑
                if(weight[i-1]<=j){
                    //比较没放这个物品时，上一轮的这个背包重量下最大价值，和放上这个物品时的最大价值
                    //放上这个物品后，还要考虑剩余背包是否能容纳物品
                    packageValue[i][j]=Math.max(packageValue[i-1][j],value[i-1]+packageValue[i-1][j-weight[i-1]]);
                }else{
                    //背包没达到能容纳的重量，就还是按照上一轮最大价值
                    packageValue[i][j]=packageValue[i-1][j];
                }

            }
        }

        //打印结果
        System.out.println("动态规划后最大的价值是："+packageValue[count][capacity]);
    }
}

控制台输出情况，显然是现在物品1和物品3价值最大，结果OK。

最后

（1）贪心解决不了就用动态规划，一般贪心算法的时间复杂度为O(nlgn)，动态规划为O(n^2)，能用贪心解决就不用动态规划。

（2）贪心得到的结果不一定是最优解。

（3）动态规划在分析子问题的时候，会使用前面子问题的最优结果，并且前面子问题的最后结果不受后面的影响，最后一个子问题即最优解。

参考博文：

（1） https://www.cnblogs.com/youngchaolin/p/11147384.html

（2） https://www.jianshu.com/p/b613ae9d77ff

（3） https://www.jianshu.com/p/86daf14620b1