题目描述
Chris家的电话铃响起了,里面传出了Chris的老师焦急的声音:“喂,是Chris的家长吗?你们的孩子又没来上课,不想参加考试了吗?”一听说要考试,Chris的父母就心急如焚,他们决定在尽量短的时间内找到Chris。他们告诉Chris的老师:“根据以往的经验,Chris现在必然躲在朋友Shermie或Yashiro家里偷玩《拳皇》游戏。现在,我们就从家出发去找Chris,一但找到,我们立刻给您打电话。”说完砰的一声把电话挂了。
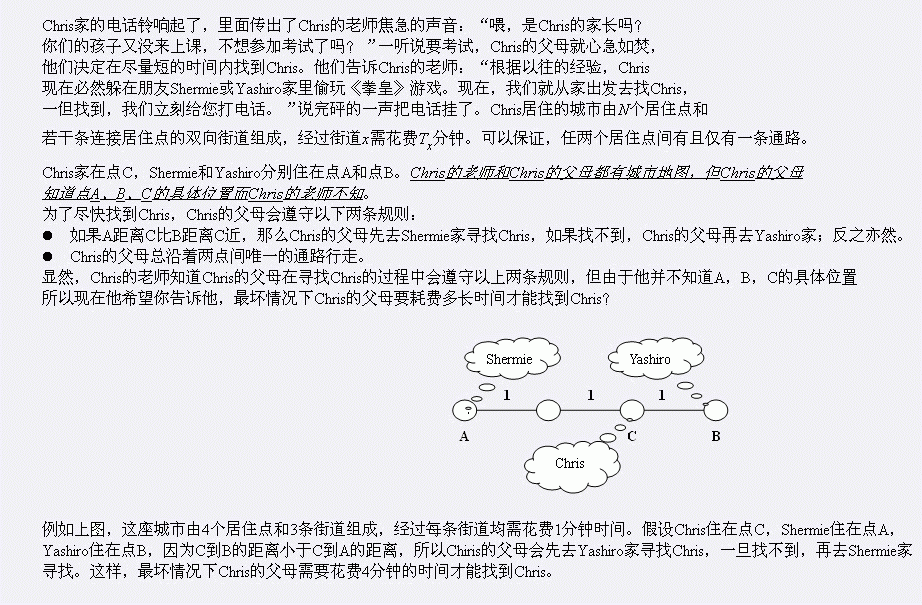
Chris居住的城市由N个居住点和若干条连接居住点的双向街道组成,经过街道x需花费Tx分钟。可以保证,任两个居住点间有且仅有一条通路。Chris家在点C,Shermie和Yashiro分别住在点A和点B。Chris的老师和Chris的父母都有城市地图,但Chris的父母知道点A、B、C的具体位置而Chris的老师不知。
为了尽快找到Chris,Chris的父母会遵守以下两条规则:
如果A距离C比B距离C近,那么Chris的父母先去Shermie家寻找Chris,如果找不到,Chris的父母再去Yashiro家;反之亦然。
Chris的父母总沿着两点间唯一的通路行走。
显然,Chris的老师知道Chris的父母在寻找Chris的过程中会遵守以上两条规则,但由于他并不知道A,B,C的具体位置,所以现在他希望你告诉他,最坏情况下Chris的父母要耗费多长时间才能找到Chris?
输入格式
输入文件第一行是两个整数(N(3 ≤ N ≤ 200000))和(M),分别表示居住点总数和街道总数。
以下M行,每行给出一条街道的信息。第(i+1)行包含整数(U_i、V_i、T_i(1≤U_i, V_i ≤ N,1 ≤ T_i ≤ 1000000000)),表示街道i连接居住点(U_i)和(V_i),并且经过街道i需花费(T_i)分钟。街道信息不会重复给出。
输出格式
输出文件仅包含整数T,即最坏情况下Chris的父母需要花费T分钟才能找到Chris。
输入样例
4 3
1 2 1
2 3 1
3 4 1
输出样例
4
题解
好久没见过思路这么简单的题了,但该WA还是要WA
首先这个图是一棵树
然后就很明确了,显然是树的直径,情况最差的时候,A点和B点之间的路径就是树的直径,然后C点就是使(min(distance_{C,A},distance_{C,B}))最大的C点.
首先DFS求出树的直径,然后遍历每一个点作为C点求出(distance_{C,A},distance_{C,B}),然后根据刚才的式子推出来即可.
有几个需要注意的点:
9 8
1 8 1000000000
8 7 1000000000
7 5 1000000000
1 3 1000000000
7 2 1000000000
1 6 1000000000
3 4 1000000000
8 9 1000000000
对于这个输入,应该输出8000000000,如果你输出的是负数说明你没有开long long.
直接些会TLE,在求距离的函数那里加一个记忆化即可
怎么感觉我写不是正解,代码也太丑了
再附赠一个数据:
输入:
4 3
1 2 1
1 3 1
1 4 2
输出:
5
代码
#include <cstdio>
#include <iostream>
#include <map>
#include <utility>
#define P pair<int, int>
using namespace std;
const int maxn = 200005;
int head[maxn], tot, maxi, n, m, ix, iy, iv;
long long maxv;
struct Edge {
int to, next;
long long value;
} edges[maxn << 1];
void add(int x, int y, long long value) {
edges[++tot].to = y;
edges[tot].next = head[x];
edges[tot].value = value;
head[x] = tot;
}
void dfs(int root, int fa, long long dis) {
if (dis > maxv) maxv = dis, maxi = root;
for (int x = head[root]; x; x = edges[x].next)
if (edges[x].to != fa) dfs(edges[x].to, root, dis + edges[x].value);
}
map<P, long long> save;
long long getd(int root, int fa, int target) {
if (root == target) return 0;
if(save.count(make_pair(root, target)))return save[make_pair(root, target)];
for (int x = head[root]; x; x = edges[x].next) {
if (edges[x].to == fa) continue;
long long r = getd(edges[x].to, root, target);
if (r != -1) {
save[make_pair(edges[x].to, target)] = r;
return r + edges[x].value;
}
}
return -1;
}
int main() {
scanf("%d%d", &n, &m);
while (m--) {
scanf("%d%d%d", &ix, &iy, &iv);
add(ix, iy, iv);
add(iy, ix, iv);
}
dfs(1, 0, 0);
int d1 = maxi;
maxv = 0, maxi = 0;
dfs(d1, 0, 0);
int d2 = maxi;
long long cmaxv = 0;
int cmaxi = 0;
for (int i = 1; i <= n; i++)
if (i != d1 && i != d2)
cmaxv = max(cmaxv, min(getd(i, 0, d1), getd(i, 0, d2)));
printf("%lld
", cmaxv + maxv);
return 0;
}