线段树（与区间有关的操作）

　

线段树（英语：Segment Tree）是一种二叉搜索树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[a,b]，它的左子树表示的区间为[a,(a+b)/2]，右子树表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树。叶节点数目为N，即整个线段区间的长度。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

线段树的基本操作：

　　　　1）建立线段树；。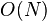

　　　　2）在区间内插入线段或者数据；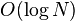

　　　　3）删除区间内的线段或者数据；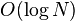

　　　　4）动态维护线段树：

　　　　　　（1）线段树单点更新的维护；

　　　　　　（2）线段树子区间更新的维护；

如果允许惰性赋值而加上延迟标记的话，许多的区间修改的时间复杂度也会是 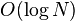，但是单点查询的时间复杂度会变成 。

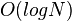代码中, rt指的是root, 当前子树的根节点; l, r指的是当前子树所统计的区间 利用完全二叉堆的性质来保存节点编号, 所以rt << 1是左子树的节点, rt << 1 | 1是右子树的节点 在查询和成端更新操作中的L和R是指修改或者查询的区间

节点数据向上更新：

将子节点的值更新到父节点。

/* 对于区间求和 */
void push_up(int rt) {
    tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}

/* 对于区间求最大值 */
void push_up(int rt) {
    tree[rt] = max(tree[rt << 1], tree[rt << 1 | 1]);
}

节点懒惰标记下推：

对于区间求和, 原子数组值需要加上lazy标记乘以子树所统计的区间长度。 len为父节点统计的区间长度, 则len - (len >> 1)为左子树区间长度, len >> 1为右子树区间长度。

void push_down(int rt, int len) {
    tree[rt << 1] += lazy[rt] * (len - (len >> 1));
    lazy[rt << 1] += lazy[rt];
    tree[rt << 1 | 1] += lazy[rt] * (len >> 1);
    lazy[rt << 1 | 1] += lazy[rt];
    lazy[rt] = 0;
}

对于区间求最大值, 子树的值不需要乘以长度, 所以不需要传递参数len。

void push_down(int rt) {
    tree[rt << 1] += lazy[rt];
    lazy[rt << 1] += lazy[rt];
    tree[rt << 1 | 1] += lazy[rt];
    lazy[rt << 1 | 1] += lazy[rt];
    lazy[rt] = 0;
}

建树：

新建一棵长度N的线段树。

#define lchild rt << 1, l, m
#define rchild rt << 1 | 1, m + 1, r
void build(int rt = 1, int l = 1, int r = N) {
    if (l == r) { std::cin >> tree[rt]; return; }
    int m = (l + r) >> 1;
    build(lchild); build(rchild);
    push_up(rt);
}

更新：

单点更新, 不需要用到lazy标记

#define lchild rt << 1, l, m
#define rchild rt << 1 | 1, m + 1, r
void update(int p, int delta, int rt = 1, int l = 1, int r = N) {
    if (l == r) {
        tree[rt] += delta;
        return;
    }
    int m = (l + r) >> 1;
    if (p <= m) update(p, delta, lchild);
    else update(p, delta, rchild);
    push_up(rt);
}

成段更新, 需要用到lazy标记来提高时间效率

#define lchild rt << 1, l, m
#define rchild rt << 1 | 1, m + 1, r
void update(int L, int R, int delta, int rt = 1, int l = 1, int r = N) {
    if (L <= l && r <= R) {
        tree[rt] += delta * (r - l + 1);
        lazy[rt] += delta;
        return;
    }
    if (lazy[rt]) push_down(rt, r - l + 1);
    int m = (l + r) >> 1;
    if (L <= m) update(L, R, delta, lchild);
    if (R > m)  update(L, R, delta, rchild);
    push_up(rt);
}

区间查询

#define lchild rt << 1, l, m
#define rchild rt << 1 | 1, m + 1, r
int query(int L, int R, int rt = 1, int l = 1, int r = N) {
    if (L <= l && r <= R) return tree[rt];
    if (lazy[rt]) push_down(rt, r - l + 1);
    int m = (l + r) >> 1, ret = 0;
    if (L <= m) ret += query(L, R, lchild);
    if (R > m)  ret += query(L, R, rchild);
    return ret;
}