[动态规划] 矩阵链乘法问题

什么是矩阵链乘法(Matrix Chain Multiplication)

矩阵链乘法问题是指给定一串矩阵序列M₁M2..Mn，求至少需要进行多少次乘法运算才能求得结果

比如对于这个M₁M₂M₃的矩阵链， 

我们可以先计算M₁M₂然后结果乘以M₃，也可以M₂M₃先算，然后乘以M₁，为了表达方便，可以用括号表示计算顺序。 矩阵链M₁M₂M₃有两种计算顺序：((M₁M₂)M₃)和(M₁(M₂M₃))。 那么不同计算顺序有什么区别？ 对于((M₁M₂)M₃): 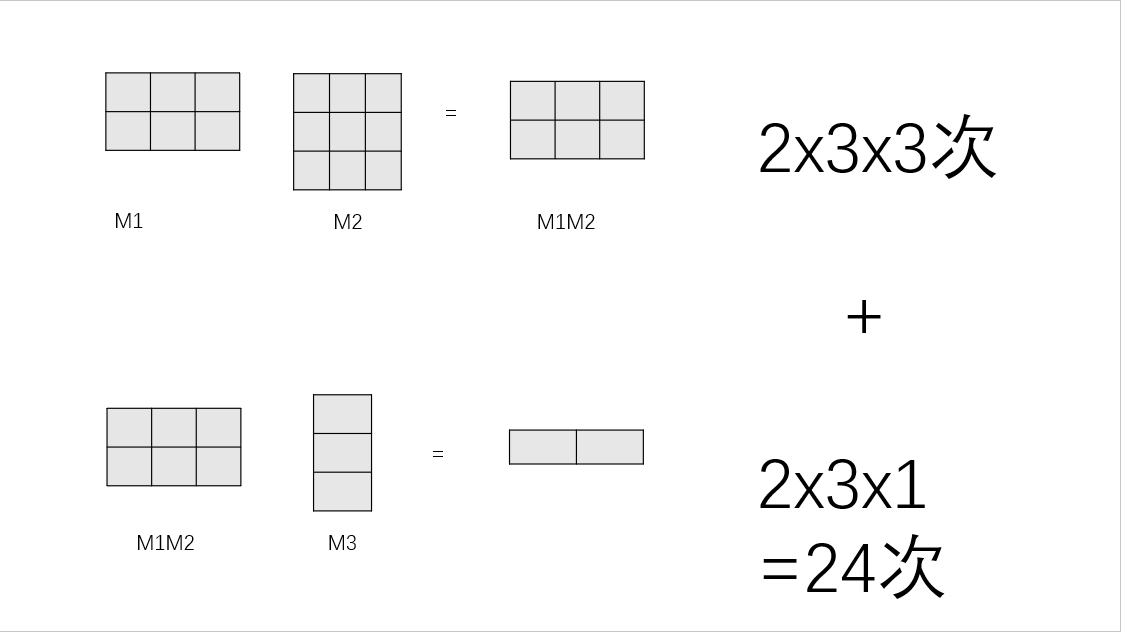对于(M₁(M₂M₃))： 

我们要做的就是找到让乘法运算最少的计算顺序，换言之就是找一种加括号方式，使得最后乘法运算最少

状态转移方程

现用 optimal(M₁M₂) 表示M₁M₂最优计算成本 cost(M₁M₂) 表示M₁M₂计算成本optimal(M₁M₂)=optimal(M₁)+optimal(M₂)+cost(M₁M₂)

optimal(M₁)和optimal(M₂)均为零；同理

optimal(M₂M₃)=optimal(M₂)+optimal(M₃)+cost(M₂M₃)

(M₁M₂M₃)有两种加括号方式， 它的最优计算成本是这两种加括号方式中最优的那个，即:optimal(M₁M₂M₃)=min{optimal((M₁M₂)M₃),optimal(M₁(M₂M₃))}

显然，这里说的正是动态规划思想：我们从局部最优解出发，逐渐构造出大问题(同时局部最优解还有重叠，可以保存计算结果免去后面计算)。状态方程已经构造出来了，下面就是实际的实现

实现

#include <iostream>
#include <algorithm>
#include <climits>

int dp[1024][1024] = { 0 };

struct Matrix {
    int row;
    int column;
};

int matrixChainCost(Matrix *ms, int n) {
    for (int scale = 2; scale <= n; scale++) {
        for (int i = 0; i <= n - scale; i++) {
            int j = i + scale - 1;
            dp[i][j] = INT_MAX;
            for (int k = i; k < j; k++) {
                dp[i][j] = std::min(dp[i][j], dp[i][k] + dp[k+1][j] + (ms[i].row*ms[k].column*ms[j].column));
            }
        }
    }
    return dp[0][n - 1];
}

int main() {
    int n;
    std::cin >> n;  //n个矩阵组成的矩阵链
    Matrix *ms = new Matrix[n];
    for (int i = 0; i<n; i++) {
        std::cin >> ms[i].row;      //第i个矩阵的行数
        std::cin >> ms[i].column;   //第i个矩阵的列数
    }
    std::cout << matrixChainCost(ms, n);
    system("pause");
    return 0;
}