题目描述:
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
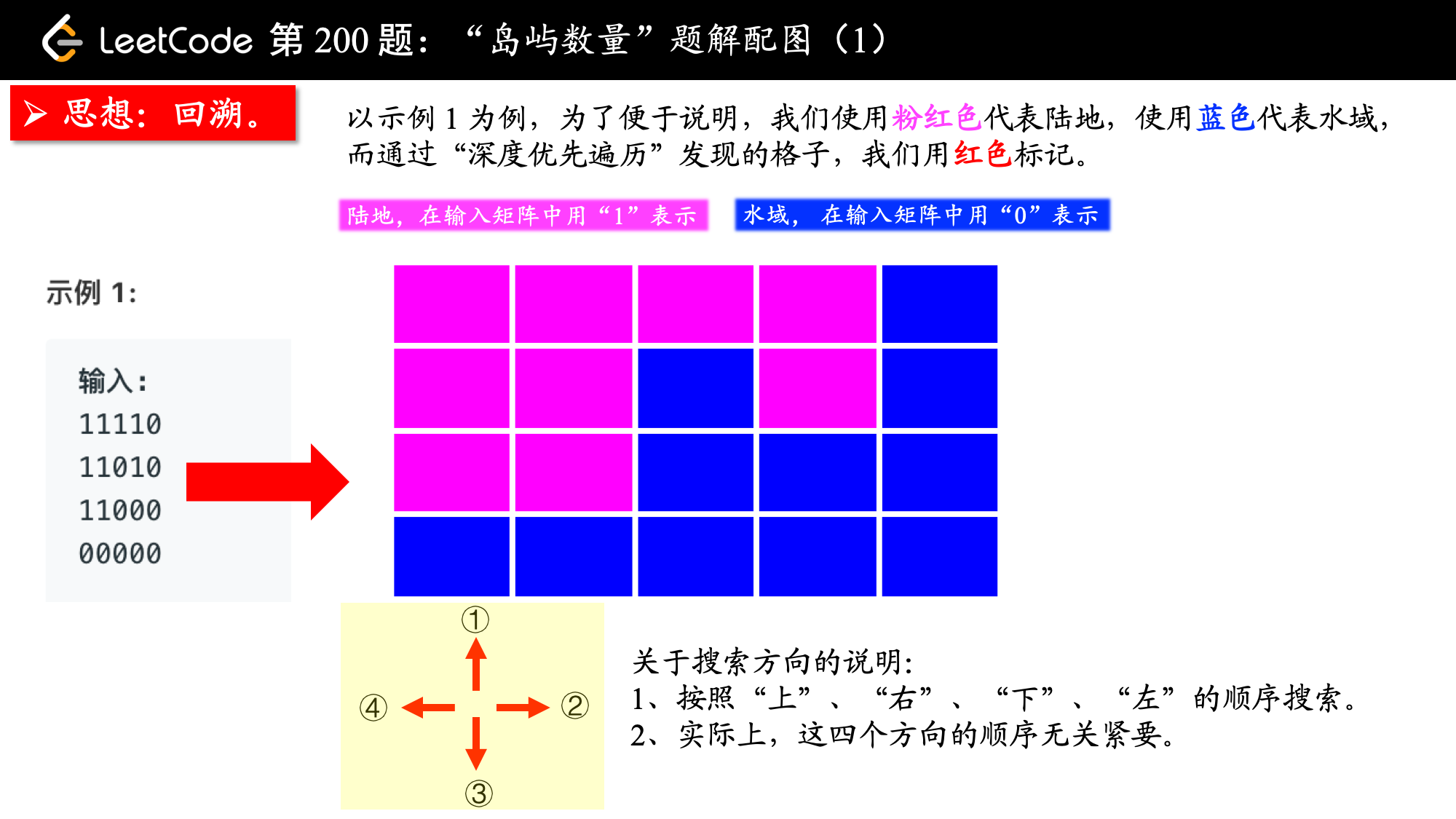
示例 1: 输入: 11110 11010 11000 00000 输出: 1 示例 2: 输入: 11000 11000 00100 00011 输出: 3
思路分析:题解和示例图来自:liweiwei1419
说明:以下介绍的算法,除了并查集以外,DFS 和 BFS 都属于很基础的算法内容,也非常好理解,写法也相对固定,读者需要多写,发现并记录自己的问题,我也是在写了几遍甚至是在写本题解的过程中,才发现出自己的问题。
这道题是可以使用一个经典的算法来解决的,那就是 Flood fill,以下的定义来自 维基百科:Flood fill 词条。
Flood fill 算法是从一个区域中提取若干个连通的点与其他相邻区域区分开(或分别染成不同颜色)的经典 算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。在 GNU Go 和 扫雷 中,Flood Fill算法被用来计算需要被清除的区域。
“Flood” 我查了一下,作为动词是 “淹没;充满” 的意思,作为名词是 “洪水” 的意思。下面我们简单解释一下这个算法:
从一个区域中提取若干个连通的点与其他相邻区域区分开
从一个点扩散开,找到与其连通的点,这不是什么高深的算法,其实就是从一个点开始,进行一次 “深度优先遍历” 或者 “广度优先遍历”,通过 “深度优先遍历” 或者 “广度优先遍历” 发现一片连着的区域,对于这道题来说,就是从一个是 “陆地” 的格子开始进行一次 “深度优先遍历” 或者 “广度优先遍历”,把与之相连的所有的格子都标记上,视为发现了一个 “岛屿”。
说明:这里做 “标记” 的意思是,通过 “深度优先遍历” 或者 “广度优先遍历” 操作,我发现了一个新的格子,与起始点的那个格子是连通的,我们视为 “标记” 过,也可以说 “被访问过”。
那么每一次进行 “深度优先遍历” 或者 “广度优先遍历” 的条件就是:
1、这个格子是陆地 1,如果是水域 0 就无从谈论 “岛屿”;
2、这个格子不能是之前发现 “岛屿” 的过程中执行了 “深度优先遍历” 或者 “广度优先遍历” 操作,而被标记的格子.
思路一:DFS
代码实现:
package com.company;
/**
* @author yaoshw
*/
public class Main {
public static void main(String[] args) {
char[][] grid2 = {
{'1', '1', '0', '0', '0'},
{'1', '1', '0', '0', '0'},
{'0', '0', '1', '0', '0'},
{'0', '0', '0', '1', '1'}};
System.out.println(numIslands(grid2));
}
public static int numIslands(char[][] grid) {
//grid的行
int row = grid.length;
if (row == 0) {
return 0;
}
//grid的列
int col = grid[0].length;
//标记grid的处于该坐标的点是否被访问
boolean[][] visited = new boolean[row][col];
//表示当前网格的四个方向,上->右->下->左
int[][] directions = new int[][]{
{-1, 0}, {0, -1}, {1, 0}, {0, 1}
};
//累加找到的岛屿数量
int count = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (grid[i][j] == '1' && !visited[i][j]) {
count++;
//从当前位置开始深度优先遍历(dfs)
dfs(i, j, directions, visited, row, col, grid);
}
}
}
return count;
}
//dfs
private static void dfs(int i, int j, int[][] directions, boolean[][] visited, int row, int col, char[][] grid) {
//标记当前节点已经被访问
visited[i][j] = true;
//此处k从0~3,表示从一个点到下一个可能的网格,求坐标
for (int k = 0; k < 4; k++) {
//下一个要走网格的x坐标
int newX = i + directions[k][0];
//下一个要走网格的Y坐标
int newY = j + directions[k][1];
//没有走越界,并且没有被访问,并且还是陆地
if (inArea(newX, newY, row, col) && !visited[newX][newY] && grid[newX][newY] == '1') {
dfs(newX, newY, directions, visited, row, col, grid);
}
}
}
//是否越界
private static boolean inArea(int newX, int newY, int row, int col) {
return newX >= 0 && newX < row && newY >= 0 && newY < col;
}
}
思路二:BFS
除了 “深度优先遍历”,你还可以使用 “广度优先遍历”,此时你就不用回溯了。“广度优先遍历” 需要一个 “辅助队列”。
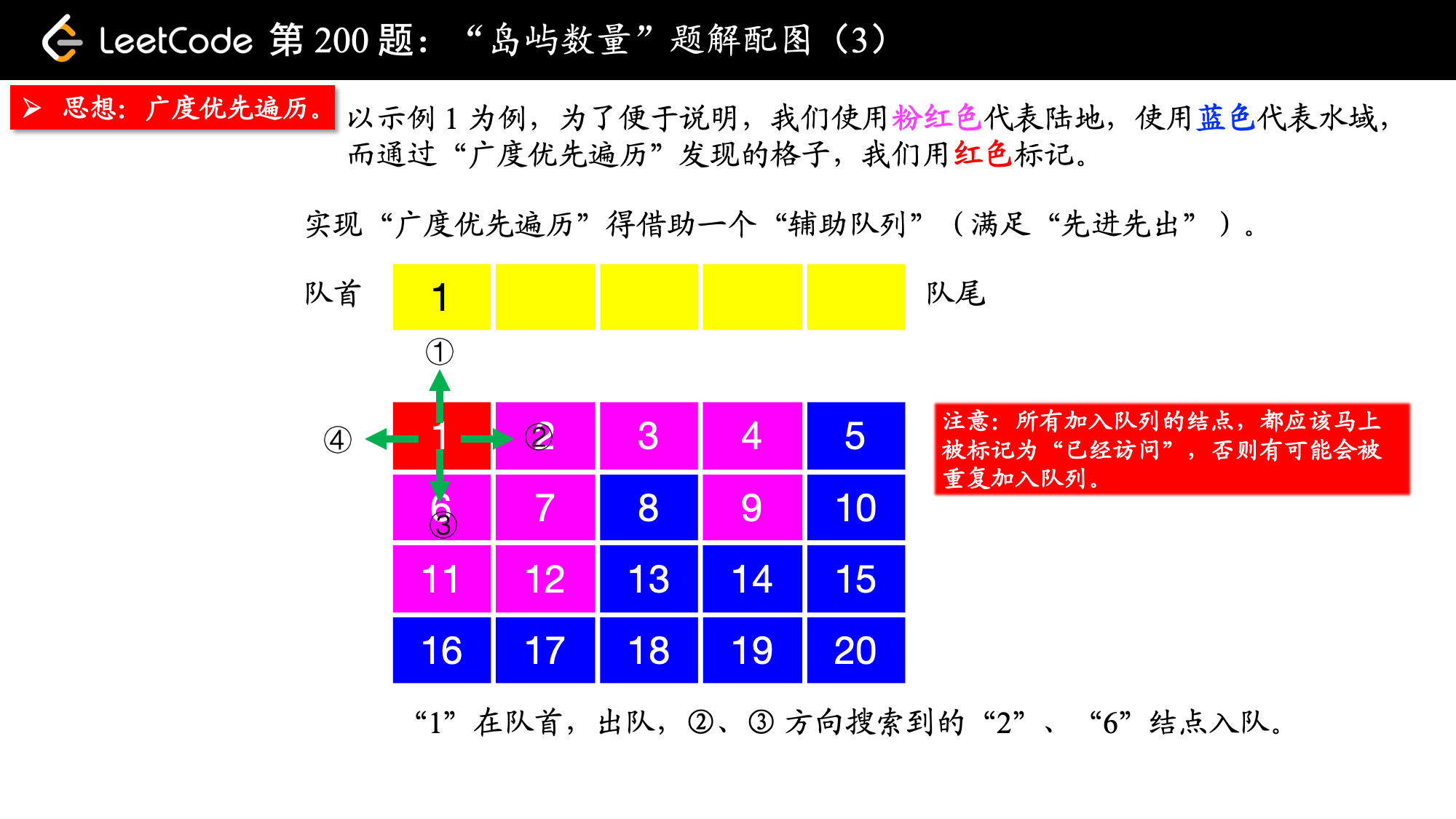
在写 “广度优先遍历” 的时候,要注意一点:所有加入队列的结点,都应该马上被标记为 “已经访问”,否则有可能会被重复加入队列。
代码实现:
/**
* 方法一:广度优先遍历
*/
public class Solution {
public static int numIslands(char[][] grid) {
//grid的行
int row = grid.length;
if (row == 0) {
return 0;
}
//grid的列
int col = grid[0].length;
//标记grid的处于该坐标的点是否被访问
boolean[][] visited = new boolean[row][col];
//表示当前网格的四个方向,上->右->下->左
int[][] directions = new int[][]{
{-1, 0}, {0, -1}, {1, 0}, {0, 1}
};
//辅助队列
Deque<Integer> helper = new LinkedList<>();
//找到的岛屿的数量
int count = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
// 如果是岛屿中的一个点,并且没有被访问过
// 从坐标为 (i,j) 的点开始进行广度优先遍历
if (grid[i][j] == '1' && !visited[i][j]) {
count++;
//此处有一个小技巧,将坐标->整数,然后加入队列,不然队列中需要放数组
helper.addLast(i * col + j);
//标记当前节点已经被访问
visited[i][j] = true;
while (!helper.isEmpty()) {
//弹出一个元素
int cur = helper.removeFirst();
//弹出元素表示的X坐标
int curX = cur / col;
//弹出元素表示的Y中标
int curY = cur % col;
//求下一个该走的网格
for (int k = 0; k < 4; k++) {
int newX = curX + directions[k][0];
int newY = curY + directions[k][1];
//是网格中的陆地,并且没有被访问,也没有越界
if (inArea(newX, newY, row, col) && !visited[newX][newY] && grid[newX][newY] == '1') {
//进队列
helper.addLast(newX * col + newY);
//标记当前节点已经被访问
visited[newX][newY] = true;
}
}
}
}
}
}
return count;
}
//是否越界
private static boolean inArea(int newX, int newY, int row, int col) {
return newX >= 0 && newX < row && newY >= 0 && newY < col;
}
}
思路三:并查集
时间复杂度:
空间复杂度: