朴素贝叶斯算法。
朴素贝叶斯是一种简单但功能强大的预测建模算法。该模型由两种类型的概率组成,可以直接从训练数据中计算:每个类的概率。每个类给定每个x值的条件概率。一旦计算出概率模型,就可以利用贝叶斯定理对新数据进行预测。
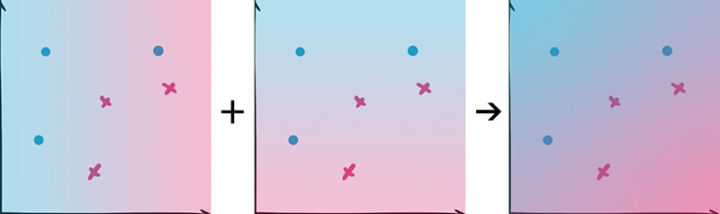
当你的数据是实值时,通常假设高斯分布(钟形曲线),这样你就可以很容易地估计这些概率。
朴素贝叶斯之所以被称为”朴素“,在于它假设每个输入变量是独立的。这是一个强硬的假设,对于真实数据来说是不切实际的,但该技术对于大范围内的复杂问题仍非常有效。
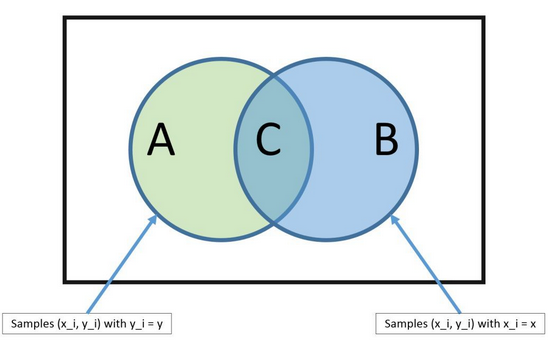
朴素贝叶斯法是是基于贝叶斯定理和特征条件独立假设的分类方法,对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合分布概率;然后基于此模型,对给定的输入x,再利用贝叶斯定理求出其后验概率最大的输出y。是一种典型的生成学习方法,其生成方法是由训练数据学习联合概率分布P(X,Y),具体来说就是利用训练数据学习P(Y)和P(X|Y)的估计:P(X,Y) = P(Y)P(X|Y),其概率估计方法是极大似然估计或者贝叶斯估计都行;另一个要注意的点是朴素贝叶斯的基本假设是条件独立性。
【有些独立假设在各个分类之间的分布都是均匀的所以对于似然的相对大小不产生影响;即便不是如此,也有很大的可能性各个独立假设所产生的消极影响或积极影响互相抵消,最终导致结果受到的影响不大。】朴素贝叶斯方法的条件独立假设看上去很傻很天真,结果却很好很强大。
吴军在数学之美系列里面介绍的隐马可夫模型(HMM)就是一个简单的层级贝叶斯模型。
Naive Bayes,核心思路是根据条件概率计算待判断点的类型。是相对容易理解的一个模型,至今依然被垃圾邮件过滤器使用。
贝叶斯过滤器纯粹根据统计学规律运作,比起那些需要分析邮件句法或内容含义的过滤器来显然要简单的多,而且可计算性强得多。更重要的是,这些标记完全可以由用户根据自己所接收的垃圾邮件和非垃圾邮件来创建,因而可以获得一种对用户来说独一无二的过滤器。这意味着垃圾邮件发送者根本无法猜测出你的过滤器是如何配置的,从而有效地阻截住各类垃圾邮件。
不过,尽管贝叶斯过滤器非常有效,但它仍需要进行优化才能真正完美。比如它可以结合 “白名单”降低误报率,结合“黑名单”降低漏过率,还可以利用其他技术如源址认证使其成为更加精确的垃圾邮件过滤器。
适用情景:
- 需要一个比较容易解释,而且不同维度之间相关性较小的模型的时候。
- 可以高效处理高维数据,虽然结果可能不尽如人意。
优点:
1.生成式模型,通过计算概率来进行分类,可以用来处理多分类问题,
2.对小规模的数据表现很好,适合多分类任务,适合增量式训练,算法也比较简单。
缺点:
1.对输入数据的表达形式很敏感,
2.由于朴素贝叶斯的“朴素”特点,所以会带来一些准确率上的损失。
3.需要计算先验概率,分类决策存在错误率。