如何评估代码的复杂度
代码具有两种复杂度衡量方向,一个是时间复杂度,一个是空间复杂度
一,时间复杂度
定义:如果一个问题的规模是n,解决这一问题的某一算法所需要的时间为T(n),它是n的某一函数T(n)称为这一算法的“时间复杂性”。
性质:
1,渐近时间复杂性:当输入量n逐渐加大时,时间复杂性的极限情形。
T(n)=O(f(n))
T(n)表示为时间复杂度
大O记法表示该函数具有上限
f(n)表示问题本身的规模n造成的时间消耗上的函数关系
2,推导大O阶方法
用常数1取代运行时间中的所有加法常数。
在修改后的运行次数函数中,只保留最高阶项。
如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
3,具体情况:
常数阶:顺序执行没有循环
线性阶:具有循环,时间复杂度和循环的次数有关
int i;
for(i = 0; i < n; i++){
/*时间复杂度为O(1)的程序步骤序列*/
}
//循环n次,总的时间复杂度是O(n)
对数阶:由于每次count乘以2之后,就距离n更近了一分。 也就是说,有多少个2相乘后大于n,则会退出循环。 由2^x=n 得到x=logn。 所以这个循环的时间复杂度为O(logn)。
int count = 1;
while (count < n){
count = count * 2;
/*时间复杂度为O(1)的程序步骤序列*/
}
平方阶:
而对于外层的循环,不过是内部这个时间复杂度为O(n)的语句,再循环n次。所以这段代码的时间复杂度为O(n^2)。如果外循环的循环次数改为了m,时间复杂度就变为O(mXn)所以我们可以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
例1:
int i, j;
for(i = 0; i < n; i++){
for(j = 0; j < n; j++){
/*时间复杂度为O(1)的程序步骤序列*/
}
}//内外循环无关,时间复杂度内外相乘
例2:
int i, j;
for(i = 0; i < n; i++){
for(j = i; j < n; j++){ /*注意j = i而不是0*/
/*时间复杂度为O(1)的程序步骤序列*/
}
}//内外循环有关系,需要逐一相加,得出关系式,并且使用大O推导,得出最终的时间复杂度:
由于当i=0时,内循环执行了n次,当i = 1时,执行了n-1次,……当i=n-1时,执行了1次。所以总的执行次数为:
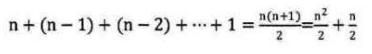
用我们推导大O阶的方法,第一条,没有加法常数不予考虑;第二条,只保留最高阶项,因此保留时(n^2)/2; 第三条,去除这个项相乘的常数,也就是去除1/2,最终这段代码的时间复杂度为O(n2)。
立方阶:
int i, j;
for(i = 1; i < n; i++)
for(j = 1; j < n; j++)
for(j = 1; j < n; j++){
/*时间复杂度为O(1)的程序步骤序列*/
}//时间复杂度是O(n^3)
4,常见的时间复杂度
常见的时问复杂度如表所示:
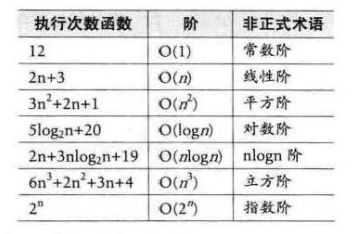
常用的时间复杂度所耗费的时间从小到大依次是:

5,最坏情况和平均情况
最坏情况运行时间是一种保证,那就是运行时间将不会再坏了。 在应用中,这是一种最重要的需求, 通常, 除非特别指定, 我们提到的运行时间都是最坏情况的运行时间。
平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。
注意:一般在没有特殊说明的情况下,都是指最坏时间复杂度。
二,空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)= O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为0(1)。//即算法计算的辅助空间是已经确定分配好的固定空间。
三,时间和空间复杂度计算规则
1,加法规则
T(n,m) = T1(n) + T2(m) = O(max{f(n), g(m)})//两个时间复杂度相加,取最大者为和
2,乘法规则
T(n,m) = T1(n) * T2(m) = O(max{f(n)*g(m)})//
3,一个经验
复杂度与时间效率的关系:
c(常数) < logn < n < n*logn < n^2 < n^3 < 2^n < 3^n < n!
l------------------------------l--------------------------l--------------l
较好 一般 较差
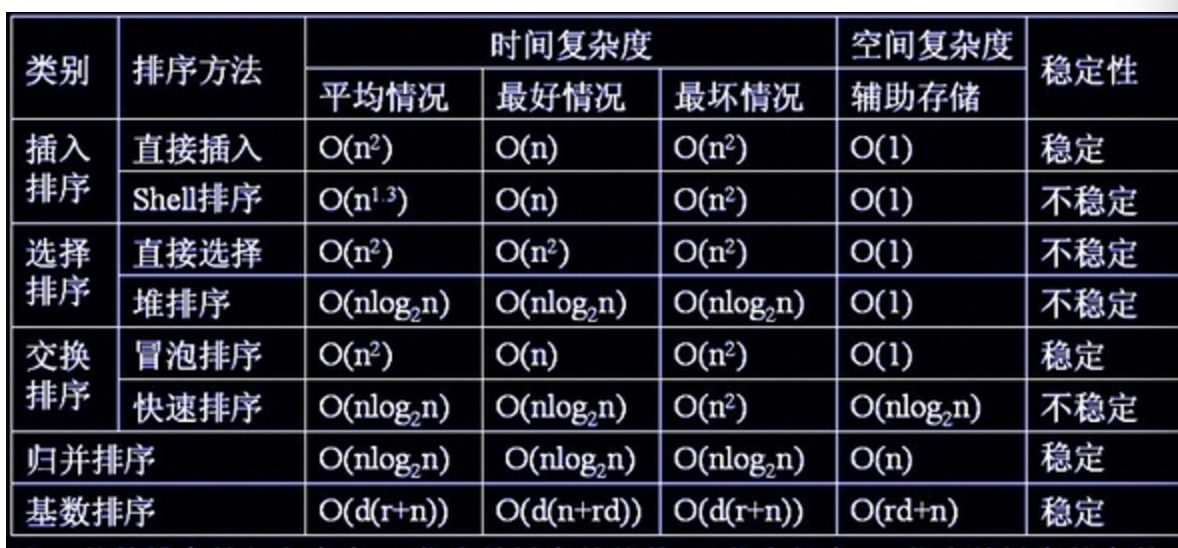
四,常用算法的时间复杂度和空间复杂度
参考文章:https://www.cnblogs.com/silence-x/p/10544072.html