题目:P2532 [AHOI2012]树屋阶梯
思路:
打表之后不难看出是裸的Catalan数。简单证明一下:
对于任意一种合法方案,都可以表示为在左下角先放一个(k*(n+1-k),kin[1,n])的矩形,再在矩形的上边和右边分别放(k-1)阶台阶和(n-k)阶台阶。
例如下图(从luogu题解中盗的图...):
在左下角先放了一个(2*3)的矩形,之后在矩形上边放(1)阶台阶,在矩形右边放(2)阶台阶。
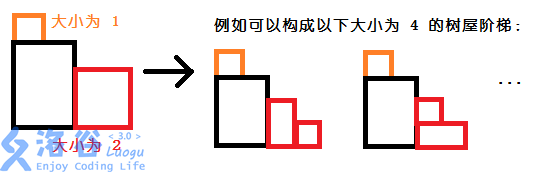
不难看出矩形上边和右边两部分独立,只要枚举左下矩阵长度,对每种矩形,把上边和右边的方案数相乘(乘法原理),再把不同矩形长度得到的答案相加(加法原理)就能得到总方案数。
设(h(n))为n阶台阶方案数,得到递推式(h(n)=sum_{k=1}^nh(k-1)*h(n-k)),就是Catalan数。
计算时分解质因数即可。
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 5000,base=10000,power=4;
int n,tot,p[N],mindiv[N],cnt[N];
struct bigint{
int len,d[N];
inline bigint (){
memset(d,0,sizeof(d));
len=1;
}
inline bigint(int num){
len=1;
d[1]=num;
}
void clean(){
while(len>1&&!d[len]) --len;
}
inline bigint operator * (const bigint &b)const{
bigint c;
c.len=len+b.len;
for(int i=1;i<=len;++i) for(int j=1;j<=b.len;++j)
c.d[i+j-1]+=d[i]*b.d[j],c.d[i+j]+=c.d[i+j-1]/base,c.d[i+j-1]%=base;
c.clean();
return c;
}
inline void print(){
clean();
printf("%d",d[len]);
for(int i=len-1;i;--i) printf("%0*d",power,d[i]);
}
};
void Prime(){
for(int i=2;i<=2*n;++i){
if(!mindiv[i]) mindiv[i]=p[++tot]=i;
for(int j=1;j<=tot;++j){
if(i*p[j]>2*n||p[j]>mindiv[i]) break;
mindiv[i*p[j]]=p[j];
}
}
}
void add(int num){
while(num^1){
++cnt[mindiv[num]];
num/=mindiv[num];
}
}
void del(int num){
while(num^1){
--cnt[mindiv[num]];
num/=mindiv[num];
}
}
bigint quickpow(int a,int b){
bigint res=1,c=a;
while(b){
if(b&1) res=res*c;
c=c*c;
b>>=1;
}
return res;
}
bigint Catalan(int n){
for(int i=n+2;i<=2*n;++i) add(i);
for(int i=1;i<=n;++i) del(i);
bigint res=1;
for(int i=1;i<=tot;++i) res=res*quickpow(p[i],cnt[p[i]]);
return res;
}
int main(){
scanf("%d",&n);
Prime();
Catalan(n).print();
return 0;
}