1 #include<iostream> 2 #include<string.h> 3 #include<algorithm> 4 using namespace std; 5 6 //问题表示 7 struct action //活动类型说明 8 { 9 int b; //活动开始时间 10 int e; //活动结束时间 11 bool operator<(const action &s) const 12 { 13 return e<=s.e; //利用sort将样例按e递增排序(类中成员e的比较大小 并返回bool型的值) <=表明当前是增序,>表明当前是降序 14 } 15 }; 16 int n=11; 17 action A[]={{0},{1,4},{3,5},{0,6},{5,7},{3,8},{5,9},{6,10},{8,11},{8,12}, 18 {2,13},{12,15}};//下标0不用 19 20 void dispA() 21 { 22 for(int i=1;i<=n;i++) 23 cout<<A[i].b<<" "<<A[i].e<<endl; 24 } 25 26 //求解结果表示 27 #define max 100 28 bool flag[max]; //标记选择的活动 29 int count=0; //选取的兼容活动个数 30 31 void slove()//求解最大兼容活动子集 32 { 33 memset(flag,0,sizeof(flag)); 34 int pend=0; //前一个兼容活动结束时间增序排序 35 for(int i=1;i<=n;i++) //扫描所有活动 36 { 37 if(A[i].b>=pend) //找到一个兼容活动 38 { 39 flag[i]=true; //选择当前活动 40 pend=A[i].e; //更新pend值 41 } 42 } 43 } 44 45 int main() 46 { 47 cout<<"求解过程:"<<endl; 48 49 cout<<"排序前:"<<endl; 50 dispA(); 51 52 sort(A+1,A+n+1); //A[1...n]排序 53 54 cout<<"排序后:"<<endl; 55 dispA(); 56 57 slove(); 58 59 cout<<"求解结果:";//输出结果 60 61 cout<<" flag:["; 62 for(int j=1;j<=n;j++) 63 if(flag[j]==true) 64 cout<<" "<<j; 65 cout<<" ]"<<endl; 66 return 0; 67 }
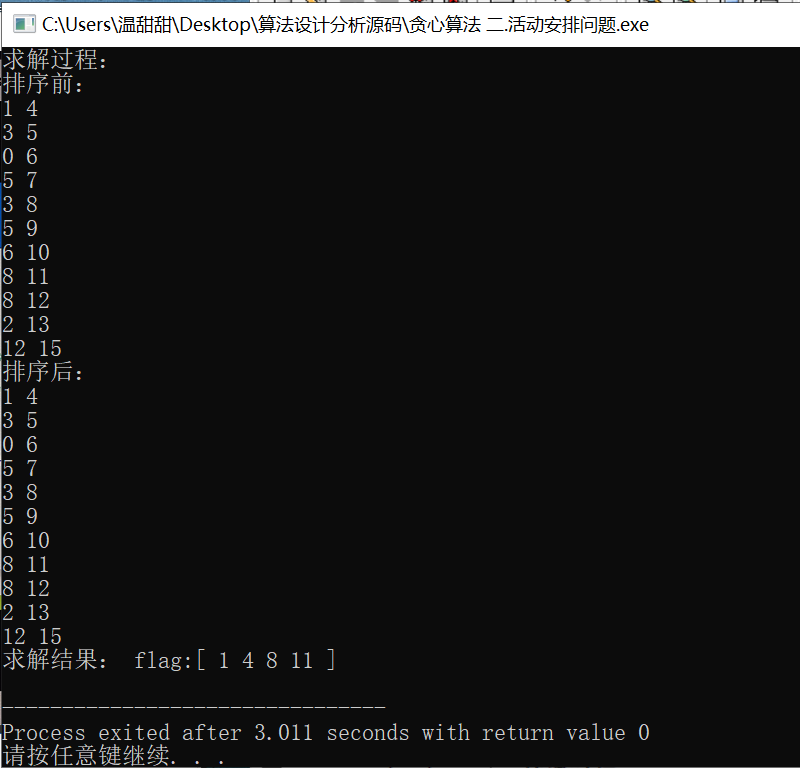
在采用不同决策的情况下,使用结束时间作为度量标准最好,因为时间不能有重叠所以结束时间越早留给后续活动的调节度就越大。