第一章 绪论(上)
(a)计算
01-a-1:计算
整个计算机科学的研究对象
计算机只是手段,计算才是最终目标
对象:规律,技巧
目标:高效,低耗
01-a-2:绳索计算机
勾股定理
01-a-3:尺规计算机
尺规做正七边形?
做不出来
尺规做正多边形的高斯判据:
N=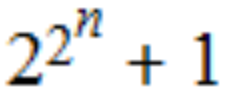
正N边形,可用尺规作图求得当且仅当
尺规作图,三等分一线段
机械执行有限的若干步,子问题,算法可套用
01-a-4:算法
外延的角度?
非退化?
01-a-5:有穷性
素因子?
hailstone序列?

程序 != 算法
死循环 || 栈溢出
设计、优化
如何评判算法优劣?
01-a-6:好算法
既要马儿快快跑
又要马儿吃得少
(b)计算模型
01-b-1:性能测度
对dsa的性能进行有效的测量
1)尺子
2)咋用
01-b-02:问题规模
将不同的问题具体实例以输入规模划分等价类来便于分析
01-b-3:最坏情况
要以算法的最坏情况来评价他
01-b-4:理想模型
实验统计会有众多影响因素导致无法准确评价算法优劣
引入图灵机模型
01-b-5:图灵机
tape:划分为许多小格初始默认为#
alphabet:字符种类有限
head:对准一格,可移动
state:小格状态反转等改变
transition function:(q,c;d,l/r,p) h停机
01-b-6:图灵机实例
非负整数加一
(<,1,0,L,<)
(<,0,1,R,>)
(>,0,0,R,>)
(>,#,#,L,H)
复位是必要的,是规范,接口
01-b-7:RAM模型
》寄存器顺序编号,总数无限
》基本操作
》》R[i] <- c R[i] <- R[R[j]] R[i] <-R[j] + R[k]
R[i] <- R[j] R[R[j]] <- R[i] R[i] <- R[j] -R[k]
IF R[i] = 0 GOTO 1 IF R[i] >0 GOTO 1 GOTO 1 STOP
简化 抽象 从实际问题脱离
把时间转化为基本操作的次数
01-b-8:RAM 实例
问题:向下取整的整除操作
算法:反复地从R[0] = 1 + c 中间去r【1】 = d
在统计下溢前,所作减法的次数x
0 r[3] <- 1
1 r[0] <- r[0] + r[3]
2 r[0] <- r[0] - r[1]
3 r[2] <- r[2] + r[3]
4 if r[0] > 0 goto 2
5 r[0] <- r[2] - r[3]
6 stop

尺子有了,怎么用呢?
c 大O记号
01 -c -1:增长速度


01-c-2:大O记号


01-c-3:高效解
》常数复杂度
O(1)
不含转向(循环、调用、递归) 必须顺序执行
》对数多项式复杂度
O(logn)


都可以转换为常系数,忽略

01-c-5:难解
指数
2^n
从O(n^c)到O(2^n)是有效解到无效解的分水岭
01-c-6:2-SUBSET
典型的NP-complete
不存在多项式算法,只能是2^n
01-c-7: 增长速度
多项式?
复杂度?
第一章 绪论(下)
(D)算法分析
01-d-1:算法分析
去粗存精的估算
正确性(不变性x单调性)+ 复杂度
迭代:级数求和
递归:递归跟踪+地推方程
猜测+验证
01-d-2:级数
算术级数:与末项平方同阶
T(n)=1+2+3+……+n=n(n+1)/2=O(n^2)




啊啊啊 概率论 啊 高数(级数) 啊
具体数学
01-d-3:循环
01-d-4 : 实例:非极端元素+起泡排序
01-d-5:正确性的证明
不变性
单调性
正确性
01-d-6:封底估算-1
当量 周长
01-d-7: 封底估算-2



算法改进威力巨大
(e)迭代与递归
01-e-1:迭代与递归
螺旋上升
分而治之
01-e-2 : 减而治之
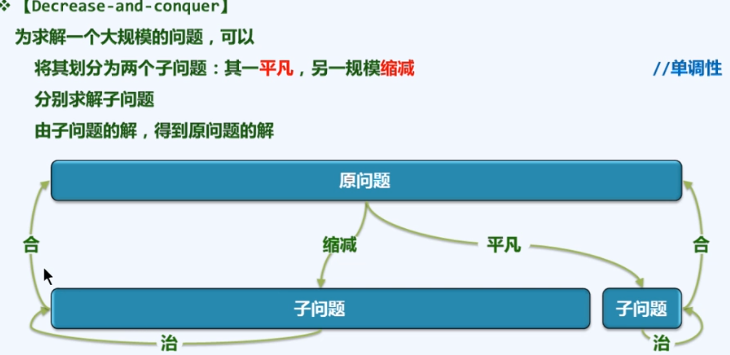
01-e-3:递归跟踪


01-e-4:递推方程
01-e-5:数组倒置
01-e-6:分而治之
01-e-7:二分递归:数组求和
01-e-8:二分递归:MAX2