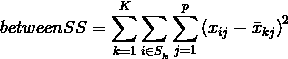在之前分享的链家二手房数据分析的练习中用到了 K-Means 聚类分析方法,所以就顺道一起复习一下 K-Means 的基础知识好了。
K-Means 聚类分析可将样本分为若干个集群,它的核心思想就是使某集群的数据点与其对应的中心之间的距离最小。所以 K-Means 聚类分析通常会假设已知集群的中心或者至少已知集群的数目。
当观测对象包含缺失值时,那么在 K-Means 聚类分析的过程中会把该观测对象除外。
比如说,对于一个有 p 个变量 n 个观察值的矩阵 X 而言,我们可以指定一个 K * P 的矩阵为初始中心,或者直接在矩阵 X 中选取 K * P 个中心。
K-Means 聚类分析包含两个重要的过程。第一个是选取初始中心,第二个是根据中心归类分组。
>> 选取初始中心
若假设将样本分为 K 个集群,那么: 1. 将前 K 个观测值设为集群中心 2. 遍历其余观测值。若该观测值与其最近的中心点的距离大于任意两个相隔最近的中心的距离,则新的观测值替代这两个原中心中距离较近的中心成为新的集群中心。说的一头雾水的吧……还是看看图吧。
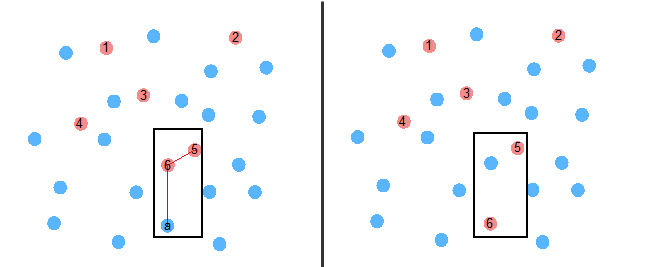
比如说,某个样本具有 6 个初始中心。当循环比较至点 a 时,可以发现点 a 到中心 6 的距离大于中心 6 与中心 5 之间的距离,于是点 a 取代离它较近的中心 6 成为新的中心。
>> 归类观测值
利用欧式距离将每个观测值归入到离它最近的集群中。

比如说将观测值 i 归入到集群 k 中,那么观测值 i 和集群 k 的距离校正值为:
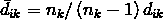
观测值和其他集群(集群 j )的距离校正值为:
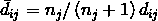
如果观测值与集群 j 的距离校正值是相较于其他集群而言最小,且小于该观测值目前所处的集群 k 的距离,那么将观测值 i 归入集群 j,并且更新每个集群的中心为其群内所有观测值的均值。
不断重复以上步骤,直至迭代次数达到上线或者两次更新中心后的集群内平方和之差小于阈值。