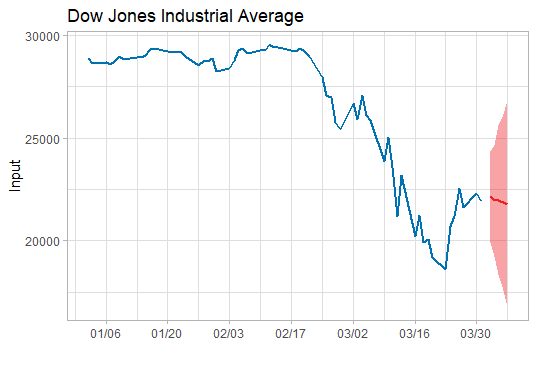
似乎突如其来,似乎合情合理,我们和巴菲特老先生一起亲见了一次,又一次,双一次,叒一次的美股熔断。身处历史的洪流,渺小的我们会不禁发问:那以后呢?还会有叕一次吗?于是就有了这篇记录:利用ARIMA模型来预测美股的走势。
1. Get Train Dataset and Test Dataset
本例子简单地以2020年第一季度的道指的收盘价为数据集(数据来源雅虎财经),将前面95%的数据用作本次预测的训练集,后面5%的数据用作本次预测的测试集。
library(quantmod)
stock <- getSymbols("^DJI", from="2020-01-01", from="2020-03-31", auto.assign=FALSE)
names(stock) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted")
stock <- stock$Close
stock <- na.omit(stock)
train.id <- 1: (0.95*length(stock))
train <- stock[train.id]
test <- stock[-train.id]
2. Stationarity Test
由于ARIMA预测要求输入数据为平稳时间序列。如果输入数据为非平稳时间序列,则需要对数据进行平稳化处理。识别数据集是否为平稳时间序列,本例子用了两种方法:1)简单粗暴的观察法;2)白噪声检验。
其实对于多次熔断向下再向下的道指来说,撇开各种观察和检验的方法,我们都知道他一定是非平稳时间序列了。下面两种方法就是打个版:当我们遇到不太明显的时间序列时可以怎么做?
2.1 Observational Method
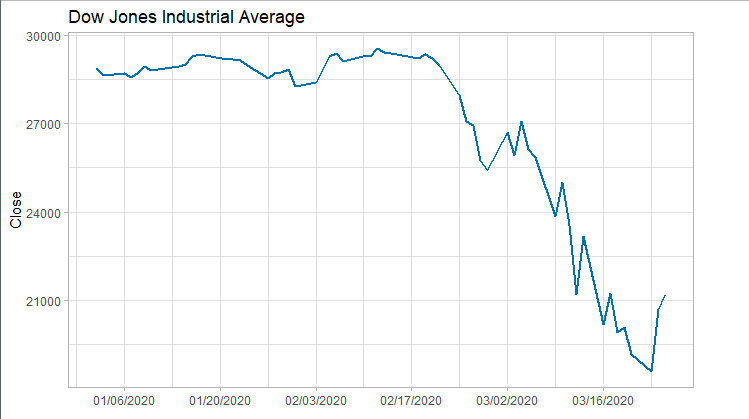
下图断崖式下降的曲线表明训练集为非平稳时间序列。
library(ggplot2)
library(scales)
plot<-ggplot(data=train) +
geom_line(aes(x=as.Date(Index), y=Close), size=1, color="#0072B2")+
scale_x_date(labels=date_format("%m/%d/%Y"), breaks=date_breaks("2 weeks"))+
ggtitle("Dow Jones Industrial Average") +
xlab("")+
theme_light()
print(plot)
2.2 Ljung‐Box Statistics Test
利用 Ljung–Box test 得到 p-value = 2.2e-16 < 0.05, 由此拒绝时间序列为白噪声的假设。
Box.test(train, lag=1, type = "Ljung-Box")
3. Differencing
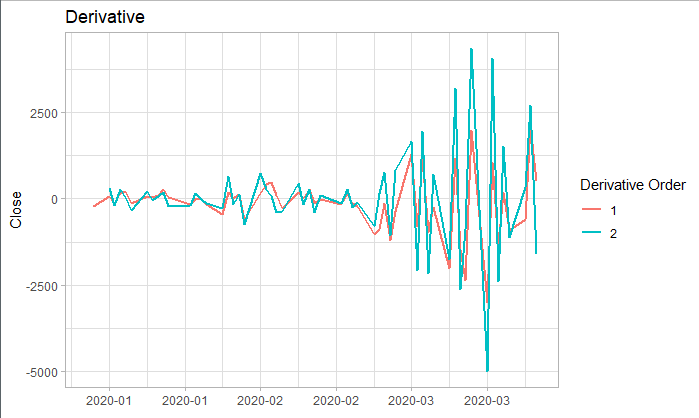
上述我们可知本训练集为非平稳时间序列,所以我们利用差分对它进行平稳化处理。对训练集分别进行一阶差分和二阶差分后,从下图其实并不能很容易看出一阶差分以及二阶差分是否为平稳序列。于是我们对其进行了ADF检验。从检验结果可知: 原序列:p-value = 0.5336 > 0.05,拒绝它是平稳序列的假设; 一阶差分:p-value = 0.4495 > 0.05,拒绝它是平稳序列的假设; 二阶差分:p-value = 0.01 < 0.05,接受它是平稳序列的假设。
所以我们将利用其二阶差分序列进行ARIMA预测。
library("tseries")
train.diff1 <- diff(train, lag = 1, differences = 1)
train.diff2 <- diff(train, lag = 1, differences = 2)
adf.test(train)
adf.test(na.exclude(train.diff1))
adf.test(na.exclude(train.diff2))
4. ARIMA Model
4.1 Choosing the order
当我们确定用二阶差分序列进行预测后,则需要对模型进行定阶。如下图所示,对于ACF,滞后1-2阶在2倍标准差外,所以q=2;对于PACF,同样也是滞后1-2阶都在2倍标准差外,所以p=2,所以将会选择模型ARIMA(2,2,2)。
acf <- acf(na.omit(train.data.diff2$Close), plot=TRUE)
pacf <- pacf(na.omit(train.data.diff2$Close), plot=TRUE)
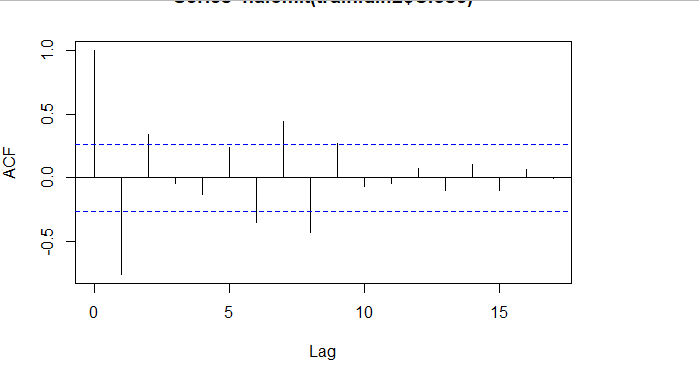
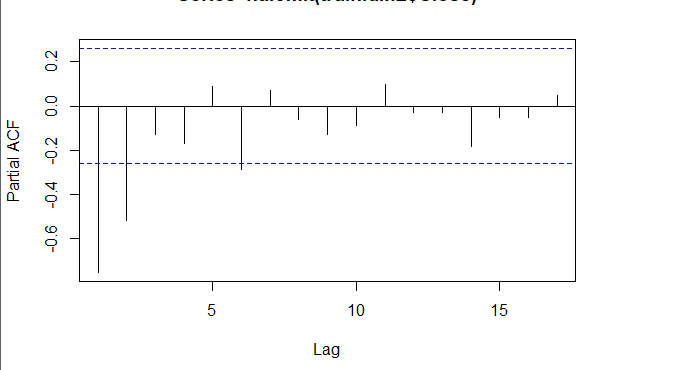
为了保证选择的模型是最优的,建议可以多选择接近的模型,然后根据AIC准则或者BIC准则选取最优的模型。比如利用自动定阶的方法,得出一个模型ARIMA(1,1,0)
library(forecast)
auto.arima(train.data,trace=TRUE) #Best model is ARIMA(1,1,0)
经过比较发现还是模型ARIMA(2,2,2)较优:
data.autofit<-arima(train.data,order=c(1,1,0))
AIC(data.autofit)
BIC(data.autofit)
data.fit<-arima(train.data,order=c(2,2,2))
AIC(data.fit)
BIC(data.fit)
| Model | AIC | BIC |
|---|---|---|
| ARIMA(1,1,0) | 930.5894 | 934.6755 |
| ARIMA(2,2,2) | 919.8881 | 930.0149 |
4.2 Model Validation
对拟合残差进行白噪声检验,得到p-value = 0.8221 > 0.05,而且acf在lag=1后迅速减小,可得残差为白噪声。
forecast <-forecast(data.fit, h=4, level=c(99.5))
forecast.data <- data.frame("Date"=index(train), "Input"=forecast$x, "Fitted"=forecast$fitted, "Residuals"=forecast$residuals)
acf(forecast.data$Residuals)
Box.test(forecast.data$Residuals, lag=sqrt(length(forecast.data$Residuals)), type = "Ljung-Box")
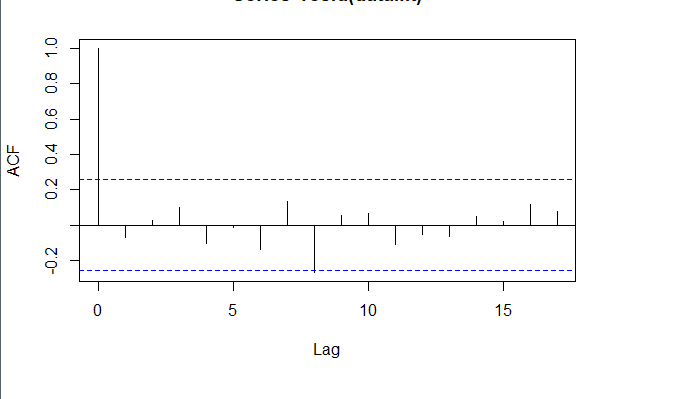
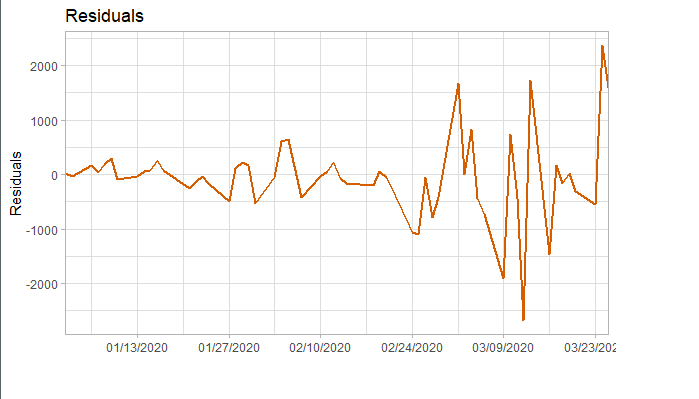
我们将训练集数据和拟合数据同时画在图上,可以看到两者的差别是在可接受范围的。
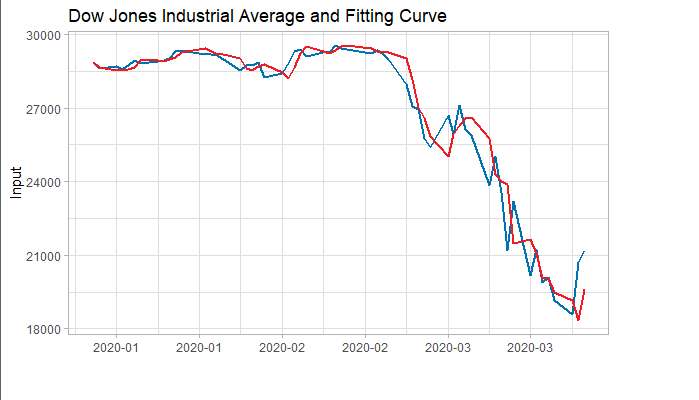
4.3 Forecast and Test Data
将预测结果与测试集对比,两者的最大相对误差为 0.056,可见模型是表达充分的,预测结果良好。
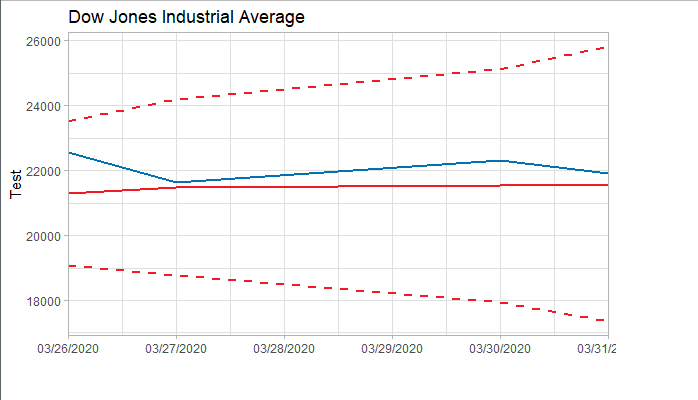
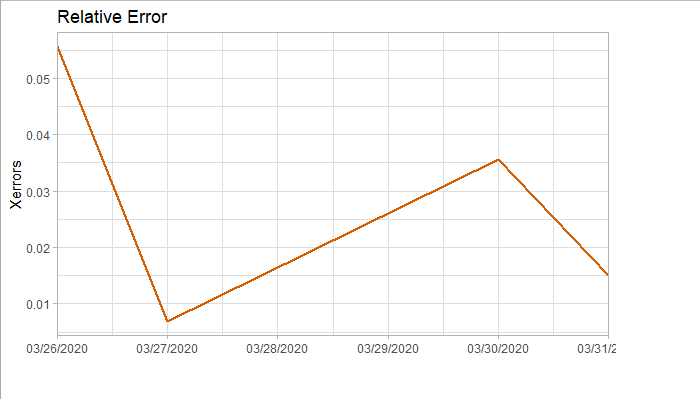
5. Forecast
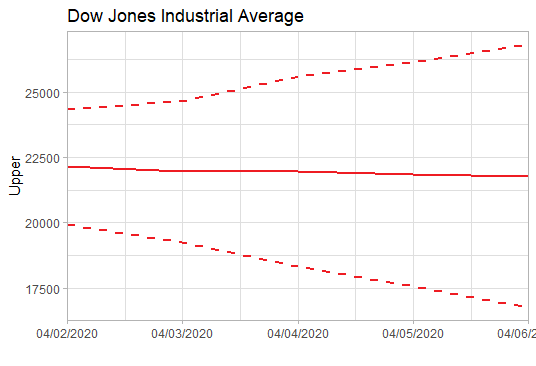
上述已经找到合适的预测模型了, 于是就可以用这个模型ARIMA(2,2,2)来预测未来5天的道指走势了。预测未来道指将在22000波动,均值微跌(呈下跌趋势),波动范围为16000-26000左右。简单说,这个模型的预测是前景不容乐观。
data.forecast<-arima(stock,order=c(2,2,2))
newforecast<-forecast(data.forecast, h=5, level=c(99.5))