【算法总结】图论-并查集
一、概念:并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题,如表示集合信息,用以实现如确定某个集合含有哪些元素、 判断某两个元素是否存在同一个集合中、求集合中元素的数量等等。常常在使用中以森林来表示。
二、并查集的原理
1.表示:
双亲结点表示法来表示一棵树,即每个结点保存其双亲结点。使用的数据结构为数组。即我们在数组单元 i 中保存结点 i 的双亲结点编号,若该结点已经是根结点则其双亲结点信息保存为-1。有了这样的存储结构,我们就能通过不断地求双亲结点来找到该结点所在树的根结点,若两个元素所在树的根结点相同,则可以判定它们在同一棵树上,它们同属一个集合。
2.合并集合:
在树的双亲结点表示法中,两树的合并即表示为其中一棵树的根节的双亲结点变为另一棵树的根结点。
3.优化——路径压缩:
我们对集合的操作主要通过查找树的根结点来实现,那么并查集中最主要的操作即查找某个结点所在树的根结点,我们的方法是通过不断查找结点的双亲结点直到找到双亲结点不存在的结点为止,该结点即为根结点。那么,这个过程所需耗费的时间和该结点与树根的距离有关,即和树高有关。在我们合并两树的过程中,若只简单的将两树合并而不采取任何措施,那么树高可能会逐渐增加, 查找根结点的耗时逐渐增大,极端情况下该树可能会退化成一个单链表。那么在 其上进行查找根结点的操作将会变得非常得耗时。
为了避免因为树的退化而产生额外的时间消耗,我们在合并两棵树时就不能 任由其发展而应该加入一定的约束和优化,使其尽可能的保持较低的树高。为了达到这一目的,我们可以在查找某个特定结点的根结点时,同时将其与根结点之间所有的结点都直接指向根结点,这个过程被称为路径压缩。
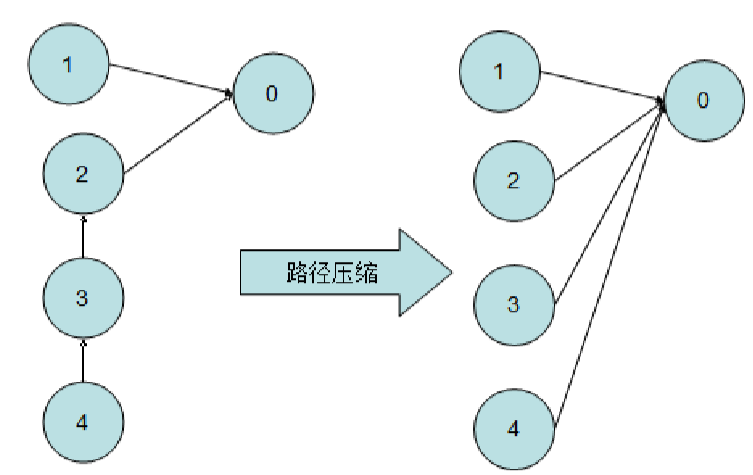
如图所示,在完成路径压缩的工作后,树的形态发生巨大改变,树高大大降低,而该树所表示的集合信息却没有发生任何改变,所以其在保证集合信息不变的情况下大大优化了树结构,为后续的查找工作节约了大量的时间。
三、并查集的数据结构
1.首先,定义一个数组,用双亲表示法来表示各棵树(所有集合元素个数总和为N)。用Tree[i]表示结点i的双亲结点,若为-1则表示其为所在树的根结点。
int Tree[N];
2.查找结点x所在树的根结点,定义如下函数(递归形式)
int findRoot(int x) { if (Tree[x] == -1)return x;//若当前节点为根结点则返回该结点号 else return findRoot(Tree[x]);//否则递归查找其双亲结点的根结点 }

int findRoot(int x) { int ret; while (Tree[x] != -1) x = Tree[x];//若不是根节点,则一直查找其双亲结点 ret = x;//返回根结点编号 return ret; }
另外若需要在查找过程中添加路径压缩的优化,修改以上两个函数为
递归形式:
int findRoot(int x) { if (Tree[x] == -1)return x;//若当前节点为根结点则返回该结点号 else { int tmp = findRoot(Tree[x]); Tree[x] = tmp;//将当前结点的双亲结点设置为查找返回的根结点编号,此时返回的已经是递归结束的根结点编号了 return tmp; } }

int findRoot(int x) { int ret; int tmp = x; while (Tree[x] != -1) x = Tree[x];//若不是根节点,则一直查找其双亲结点 ret = x;//返回根结点编号 x = tmp;//再做一次从结点x到根结点的遍历,较为繁琐 while (Tree[x] != -1) { int t = Tree[x]; Tree[x] = ret; x = t;//遍历过程中将这些结点的双亲结点设置为已经查找得到的根结点编号 } return ret; }
例5.1 畅通工程
解题思路
该问题可以被抽象成在一个图上查找连通分量(彼此连通的结点集合)的个数,我们只需求得连通分量的个数,就能得到答案(新建一些边将这些连通分量连通)。这个问题可以使用并查集完成,初始时,每个结点都是孤立的连通分量,当读入已经建成的边后,我们将边的两个顶点所在集合合并,表示这两个集合中的所有结点已经连通。对所有的边重复该操作,最后计算所有的结点被保存在几个集合中,即存在多少棵树就能得知共有多少个连通分量(集合)。
AC代码

#include<cstdio> using namespace std; const int N = 1000; int Tree[N]; int findRoot(int x) { if (Tree[x] == -1)return x; else { int tmp = findRoot(Tree[x]); Tree[x] = tmp; return tmp; } } int main() { int n, m; while (scanf("%d", &n) != EOF && n != 0) { scanf("%d", &m); for (int i = 1; i <= n; i++)Tree[i] = -1;//初始时,所有结点都是孤立的,即其所在集合只有一个结点,自身即为根结点 while (m-- != 0)//读入边信息 { int a, b; scanf("%d%d", &a, &b); a = findRoot(a); b = findRoot(b);//查找边的两个顶点所在集合的信息 if (a != b) Tree[a] = b;//将有道路连接的结点集合合并 } int ans = 0; for (int i = 1; i <= n; i++) { if (Tree[i] == -1)ans++;//统计集合数目 } printf("%d ", ans - 1);//在ans个集合之间修建ans-1条道路 } return 0; }
例 5.2 More is better
题目大意
有10000000个小朋友,他们之中有N对好朋友,且朋友关系具有传递性:若A与B是朋友,B与C是朋友,那么我们也认为A与C是朋友。 在给出这 N 对朋友关系后,要求我们找出一个最大(人数最多)的集合,该集合中任意两人之间都是朋友或者该集合中只有一个人,输出该最大人数。
解题思路
如前例所示,我们利用并查集相关操作已经可以求得有几个这样符合条件的集合,但是计算集合中的元素个数我们仍没有涉及。我们如果能够成功求得每个集合的元素个数,我们只需要选择包含元素最多的集合,并输出该集合中的元素个数即可。
为了计算每个集合的元素个数,我们不妨在表示每个集合的树的根结点记录该集合所包含的元素个数,在合并时累加被合并两个集合包含的元素个数。最后, 找出所有集合中所包含元素最多的集合即是所求。
AC代码

#include<cstdio> using namespace std; const int N = 10000001; int Tree[N]; int findRoot(int x) { if (Tree[x] == -1)return x; else { int tmp = findRoot(Tree[x]); Tree[x] = tmp; return tmp; } } int sum[N];//用sum[i]表示以结点i为根的树的结点个数,其中保存数据仅当Tree[i]为-1即该结点为树的根结点时有效 int main() { int n; while (scanf("%d", &n) != EOF) { for (int i = 1; i < N; i++)//初始化结点信息 { Tree[i] = -1;//所有结点为孤立集合 sum[i] = 1;//所有集合的元素个数为1 } while (n-- != 0)//读入边信息 { int a, b; scanf("%d%d", &a, &b); a = findRoot(a); b = findRoot(b);//查找边的两个顶点所在集合的信息 if (a != b) { Tree[a] = b;//将有道路连接的结点集合合并 sum[b] += sum[a];//合并结点时,把将成为子树的树的根结点上保存的集合元素个数转移到合并后新树的树根 } } int ans = 1;//答案至少为1 for (int i = 1; i <= N; i++) { if (Tree[i] == -1 && sum[i] > ans)ans = sum[i];//统计最大值 } printf("%d ", ans); } return 0; }
