在介绍了前面的三种基本算法之后,今天说说另一种稍微高级一点的算法--希尔排序
希尔排序是按照其设计折希尔(Donald Shell)的名字命令,它基于插入算法,在插入算法上做了改造,那么插入算法有什么特点呢,我们回想一下:
1. 插入排序在已经排好序的序列上效率非常高,时间复杂度O(n),但是在最坏的情况下时间复杂度为O(n2)
2. 插入排序在做移动的时候效率是非常低的,因为每次只能移动一位
基本思想:
先选取小于N的整数d1,把数组中所有距离为d1的倍数值归为一组,先后在各组中进行插入排序,然后选择第二个整数d2<d1作为第二个增量,在将整个数列距离为d2的整数倍归为一组,再在组内进行插入排序,知道增量为1,至此整个数据将会排好顺序;
希尔排序算法使用的gap也就是d1、d2.。。为d1 = lenght/2 d2=d1/2 ,最好我们会说明其他的更高效的分组阀值
希尔排序图:
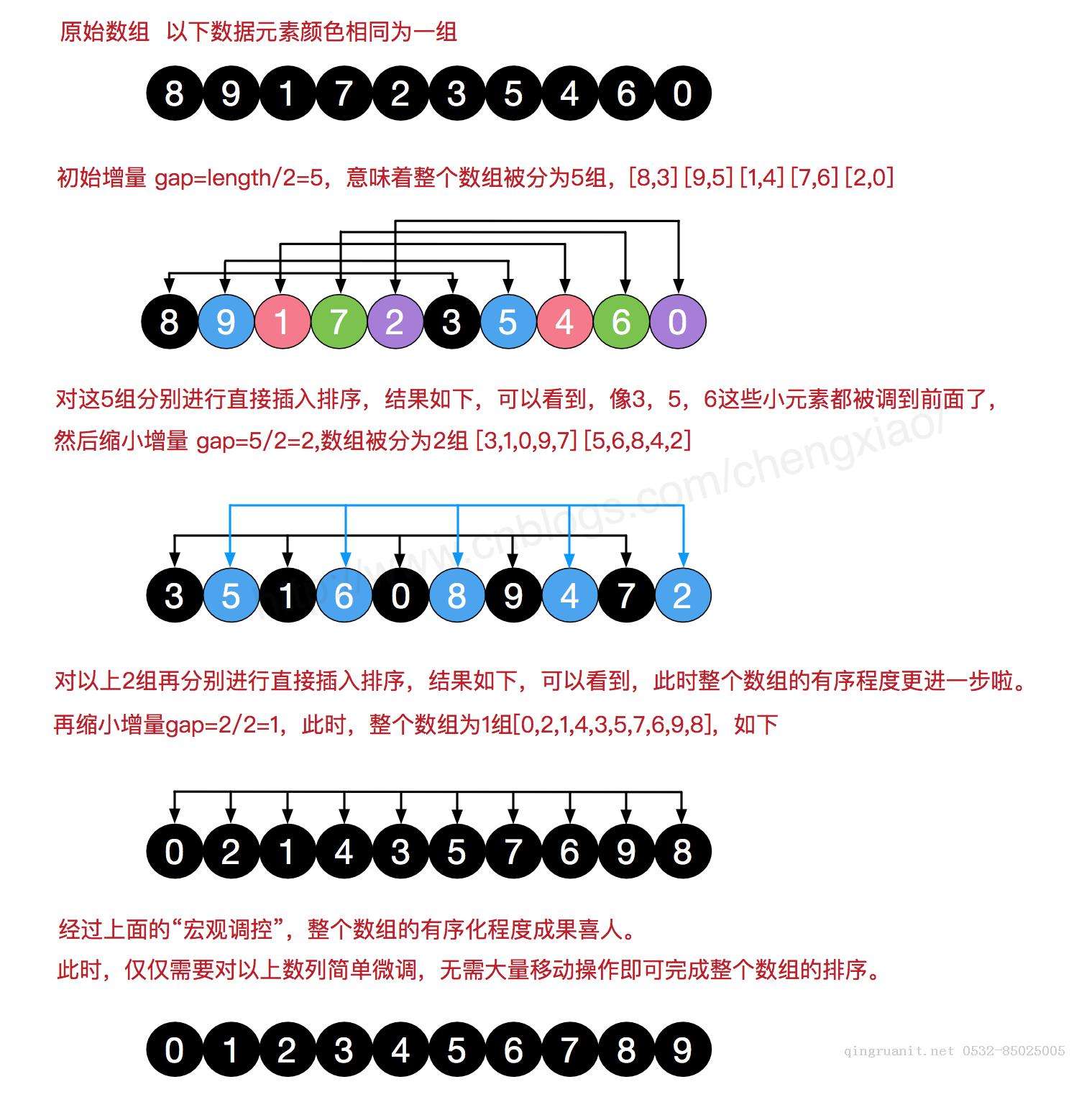
1. 在图中我们可以看到,未排序的原始数组长度为10,第一次迭代我们选择gap为length/2=5,
2. 则我们将整个数组分为5组,在图中我们可以清晰看到(8,3)为一组(9,5)为一组,以此类推
3. 我们在每组内进行插入排序,则排序后的结果就是第三个图中所示,之后我们在继续分组,gap = 5/2 = 2,表示整个数列被分成两组
4. 继续使用直接插入排序,对两组数据进行直接插入排序,以此执行分组,排序,再分组、再排序,知道gap=1,则整个数组排序完成
那么实现一下代码:
/** * 希尔排序 * 将数组分成N组,N组内使用插入排序,经过m次后,数须有序 * 希尔排序的曾量序列对排序性能致关重要,我们采用的N/2这种曾量,其最终时间复杂度还是o(n2) * 可以使用其他增量比如 Hibbard,可以使时间复杂度缩小到O(n3/2),Sedgewick时间复杂度O(n4/3) */ public class ShellSort { public static void shellsort(int[] arr) { long start = System.currentTimeMillis(); //使用length/2的gap值,知道gap=1 for (int gap = arr.length / 2; gap > 0; gap /= 2) { for (int i = gap; i < arr.length; i++) { int j = i; // 使用直接插入排序,依次对数列中每个元素和该元素同组元素进行直接插入排序 while (j - gap >= 0 && arr[j] < arr[j - gap]) { int tmp = arr[j]; arr[j] = arr[j - gap]; arr[j - gap] = tmp; j -= gap; } } } System.out.printf("直接插入算法 运行时间%dms ", (System.currentTimeMillis() - start)); } public static void main(String[] args) { int data_len = 10000; int[] data = new int[data_len]; Random rd = new Random(); for (int index = 0; index < data_len; index++) { data[index] = rd.nextInt(10000); } System.out.println("生成数据完成"); shellsort(data); showData(data); } public static void showData(int[] data) { for (int item : data) { System.out.printf("%d,", item); } System.out.println(); } }
在代码中我进行了简单注释,从gap开始遍历所有数据元素,让该元素和同组元素进行直接插入排序,知道gap=1
从直观的感觉上什么决定了希尔排序的性能呢,那就是我们选择gap的算法,代码我们使用了 gap = length/2 的初始值,该算法并非是最优的,但是很好理解,也希尔排序推荐的,但是我们可能追求极至,那么可以网上查一下其他gap生成算法,使用最多的应该是
注释中提到的 Hibbard