IOU重合率计算

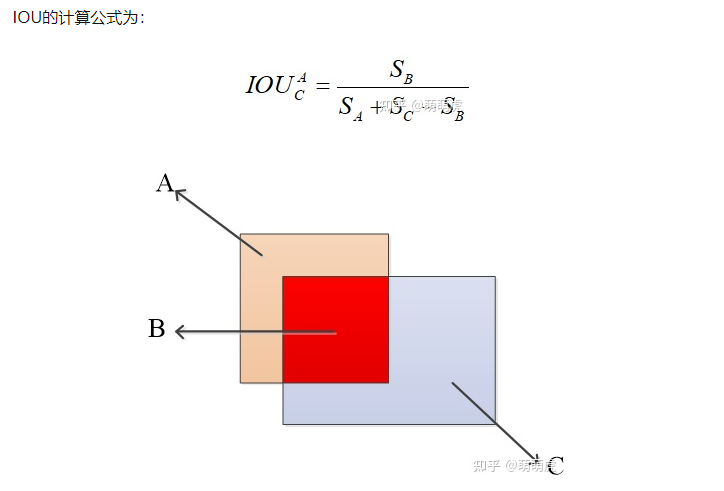
原理

python实现代码

def calculate_IoU(predicted_bound, ground_truth_bound):
    """
    computing the IoU of two boxes.
    Args:
        box: (x1, y1, x2, y2),通过左上和右下两个顶点坐标来确定矩形
    Return:
        IoU: IoU of box1 and box2.
    """
    px1, py1, px2, py2 = predicted_bound
    # print("预测框P的坐标是：({}, {}, {}, {})".format(px1, py1, px2, py2))

    gx1, gy1, gx2, gy2 = ground_truth_bound
    # print("原标记框G的坐标是：({}, {}, {}, {})".format(gx1, gy1, gx2, gy2))

    parea = (px2 - px1) * (py1 - py2)  # 计算P的面积
    garea = (gx2 - gx1) * (gy1 - gy2)  # 计算G的面积
    # print("预测框P的面积是：{}；原标记框G的面积是：{}".format(parea, garea))

    # 求相交矩形的左上和右下顶点坐标(x1, y1, x2, y2)
    x1 = max(px1, gx1)  # 得到左上顶点的横坐标
    y1 = min(py1, gy1)  # 得到左上顶点的纵坐标
    x2 = min(px2, gx2)  # 得到右下顶点的横坐标
    y2 = max(py2, gy2)  # 得到右下顶点的纵坐标

    # 利用max()方法处理两个矩形没有交集的情况,当没有交集时,w或者h取0,比较巧妙的处理方法
    # w = max(0, (x2 - x1))  # 相交矩形的长，这里用w来表示
    # h = max(0, (y1 - y2))  # 相交矩形的宽，这里用h来表示
    # print("相交矩形的长是：{}，宽是：{}".format(w, h))
    # 这里也可以考虑引入if判断
    w = x2 - x1
    h = y1 - y2
    if w <= 0 or h <= 0:
        return 0

    area = w * h  # G∩P的面积
    # print("G∩P的面积是：{}".format(area))

    # 并集的面积 = 两个矩形面积 - 交集面积
    IoU = area / (parea + garea - area)

    return IoU