给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
这道题其实不是特别的难,基本上只需要寻找其中的规律就可以了,我在做这道题的时候一共用了一下两种方法
解法一
其中最直观的一种解法是旋转矩阵,我们只需要观察一下在旋转矩阵的过程中,其中的元素是怎么被替换的!
让我们看一下下面这张图
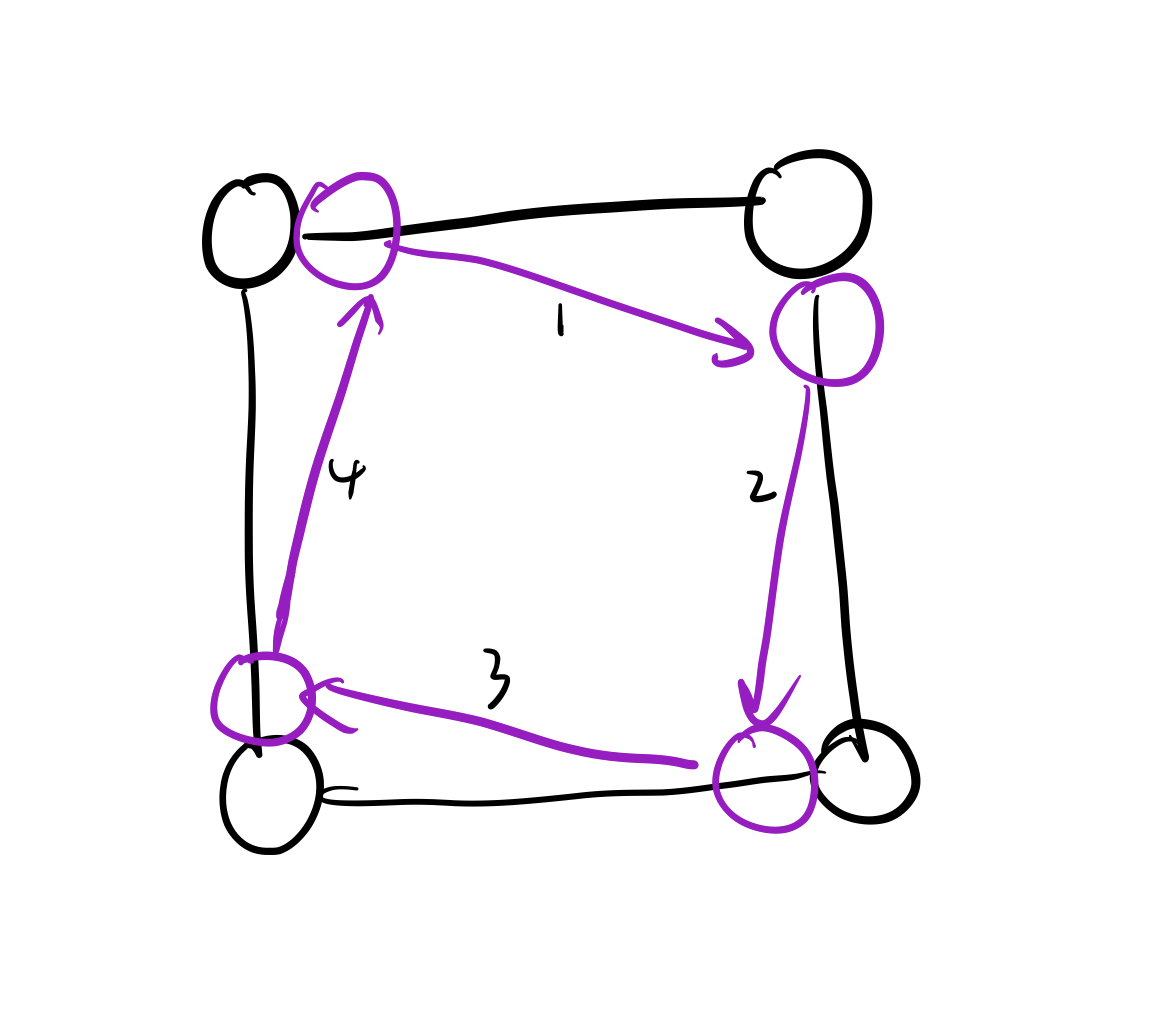
这张图什么意思呢,其实就是说,我们要旋转矩阵,其实就是要旋转矩阵之中的元素
以示例1为例:

我们先从矩阵的四个角开始,因此我们可以发现现在数字3所在位置应该被1代替,数字9的位置应该被3代替,以此类推,其实这个也说明不了什么,我们再选取下一组元素,即图中用紫色的线条圈起来的内容,同样的,这一组数据也应该在顺时针方向上做一次旋转
因此我们只需要总结出这四个点的坐标规律即可,可以得到下图
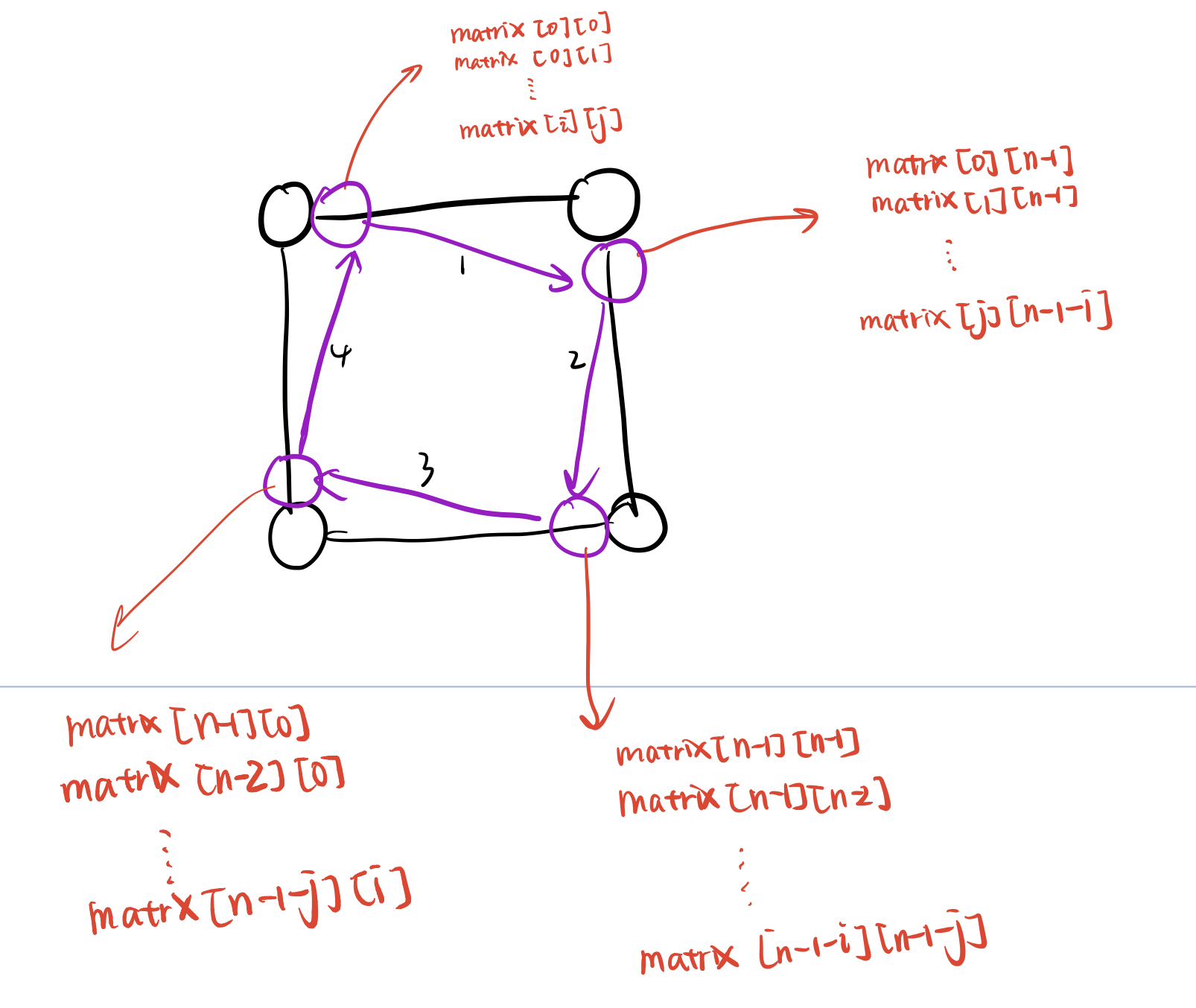
其实我得到规律的方式还是蛮原始的,只要稍微列出一两个情况就可以了,至于什么时候用i什么时候用j,我们可以这么考虑,我们这个代码应该有个基本的架构是两层循环,最内层的循环应该是对一列或者一行进行扫描,假设内层计数的变量名为j,我们就可以知道如果是matrix[0][0]、matrix[0][1],那么实际上就应该是matrix[0][j](这里可能解释的不是特别清楚),我们不可能永远都停留在第0行,所以另一个应该是变量i,因此有matrix[i][j]
再来看一下i和j怎么取值
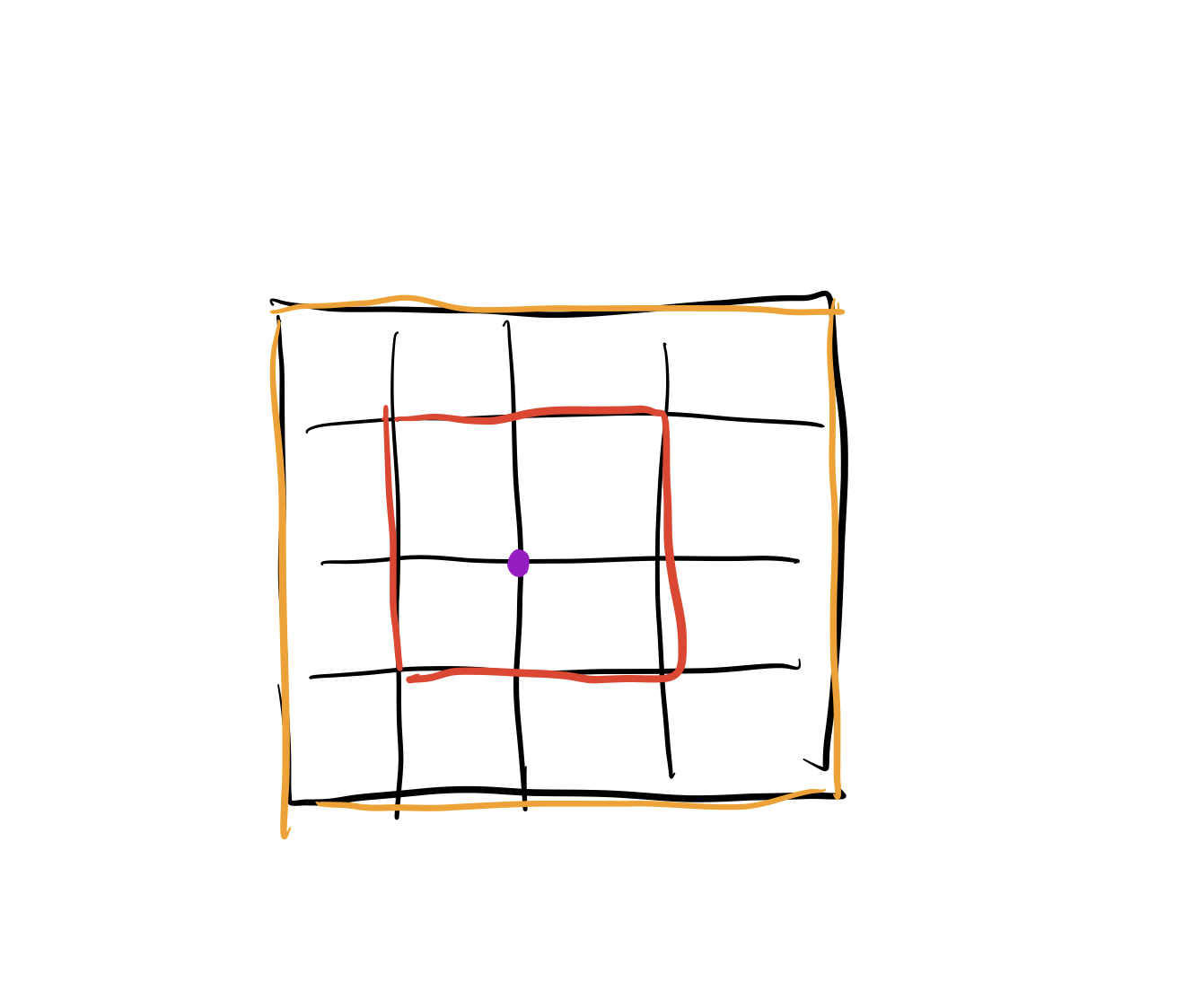
我们可以看到我们在进行矩阵旋转的时候应该是一圈一圈进行的,看起来是不是有点像撕一块面包皮的过程,以上图5x5的矩阵为例,我们一共要走三个圈,而最小的那个圈实际上是一个点,所以我们只需要走两圈就可以了,因此我们可以很快得到数学关系n/2
最后按照这个思路我们就可以得到代码
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
int temp;
for(int i = 0; i < n/2; i++){
for(int j = i; j < n-1-i; j++){
temp = matrix[j][n-1-i];
matrix[j][n-1-i] = matrix[i][j];
matrix[i][j] = matrix[n-1-j][i];
matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
matrix[n-1-i][n-1-j] = temp;
}
}
};
不过按照这个方法跑起来速度确实不太ok,因此我根据其他人的题解对自己的方法做了一些修改
解法二
其实我们只需要做三次交换就可以得到同样的效果,正如下图所示
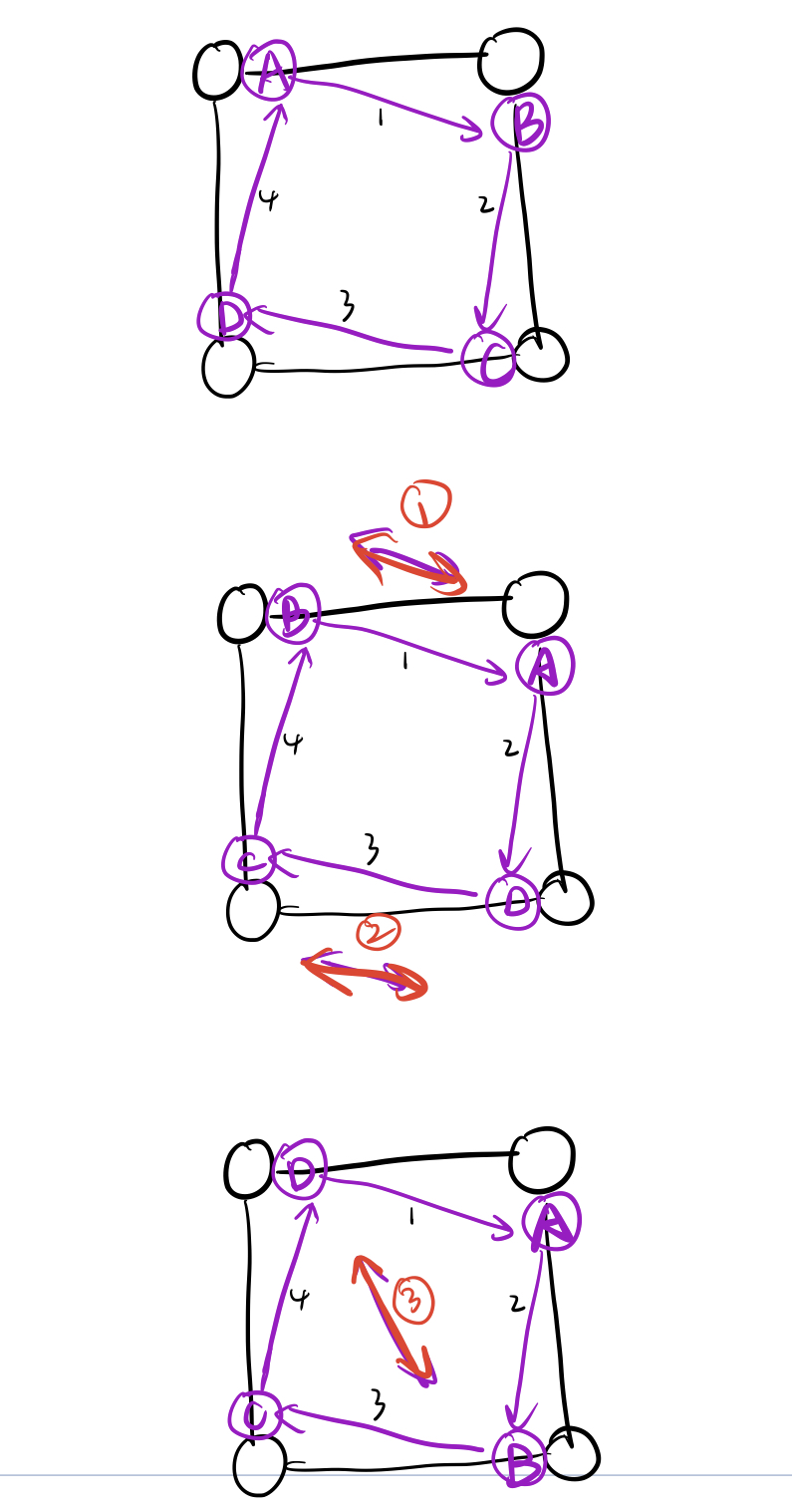
先交换A和B,再交换C和D,最后交换B和D
具体代码如下:
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
int temp;
for(int i = 0; i < n/2; i++){
for(int j = i; j < n-1-i; j++){
swap(matrix[i][j], matrix[j][n-1-i]);
swap(matrix[n-1-i][n-1-j], matrix[n-1-j][i]);
swap(matrix[n-1-i][n-1-j], matrix[i][j]);
}
}
}
};