LeetCode: 【L4】N-Queens 解题报告

【L4】N-Queens 解题报告

N-Queens Total Accepted: 16418 Total Submissions: 63309 My Submissions
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.



Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[
 

[".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

经典的八皇后问题。
SOLUTION 1：
<此题的难度级别为LEVEL-4>
使用DFS来求解。
主页君写了二个版本来求解。
第一个版本，放置一个皇后之后，从某皇后之后找所有的可能的放置点。这样在Eclipse中可以测试通过，但是
过不了Leetcode的检查。也就是说复杂度过高了。
解法1

 

SOLUTION 2：
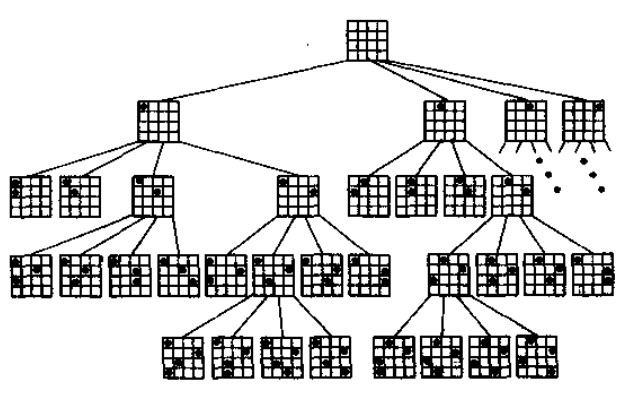
后来查资料后，得知为了加快搜索速度，我们应该以这样的思路来思考：
1. 假如我们要放置8个皇后，皇后是会攻击同行的，所以8行必须一行放置一个皇后。
    所以前面主页君从某个皇后一直搜索到最后是没有必要的。我们要做的是：放置好一个皇后后，搜索下一行中
能否再放一个皇后，如果是不可以，直接就能返回了。这样子可以节省大量的计算量：



主页君代码如下：
GitHub代码链接

December 17th, 重写如下：

 

public class Solution {
    public List<String[]> solveNQueens(int n) {
        List<String[]> ret = new ArrayList<String[]>();
        
        if (n == 0) {
            return ret;
        }
        
        dfs(n, new ArrayList<Integer>(), ret);
        return ret;
    }
    
    public String[] createSolution(ArrayList<Integer> path) {
        /*
        [
         [".Q..",  // Solution 1
          "...Q",
          "Q...",
          "..Q."],
        
         ["..Q.",  // Solution 2
          "Q...",
          "...Q",
          ".Q.."]
        ]
        */
        int size = path.size();
        String[] ret = new String[size];
        
        for (int i = 0; i< size; i++) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < size; j++) {
                // a queen.
                if (j == path.get(i)) {
                    sb.append('Q');
                } else {
                    sb.append('.');
                }
            }
            
            ret[i] = sb.toString();
        }
        
        return ret;
    }
    
    //ArrayList<Integer> path: store the index of the columns of one solution.
    public void dfs(int n, ArrayList<Integer> path, List<String[]> ret) {
        if (path.size() == n) {
            String[] solution = createSolution(path);
            ret.add(solution);
            return;
        }
        
        for (int i = 0; i < n; i++) {
            // Judge if this is a solution;
            if (!isValid(path, i)) {
                continue;
            }
            
            path.add(i);
            dfs(n, path, ret);
            path.remove(path.size() - 1);
        }
    }
    
    public boolean isValid(ArrayList<Integer> path, int index) {
        int size = path.size();
        for (int i = 0; i < size; i++) {
            // Same column as one queen.
            if (index == path.get(i)) {
                return false;
            }
            
            // 在两条对角线之上
            // bug 3: 少一个)
            if (size - i == Math.abs(index - path.get(i))) {
                return false;
            }
        }
        
        return true;
    }
}

步骤：
1. 建立一个arraylist存储每一行的皇后的列值。
例如：第一行皇后在第三列，第二行皇后在第五列，我们会记录3，5在arraylist中，依次这样推下去。
2. 进入DFS后，首先判断array是不是满，满的话说明8个皇后都放好了，创建一个解并返回。
3. 如果没有满，扫描当前行所有的位置，查找是不是能放一个皇后。如果可以放，继续DFS。不能放的话，就退出就好了。

虽然本题了解了思路后，写出来并不难，但主页君认为难点是在于：你怎么能思考到一行一行放皇后？而不是放好一个再找下一个可能放的点？如果想清楚了这一点也就不难了。
LEVEL 4还是实至名归的。