Tarjan学习笔记(1)

TARJAN:

编者的话?:

众所周知,Robert Tarjan是为著名的科学家,他不仅在求解双连通分量和强连通分量有卓越贡献,且提出了各种具有价值的,且只能是交给大佬学习的东西(splay,lint-cut tree)......

这一节我只打算按照《算法进阶竞赛指南》的顺序,先说说有关无向图的一些相关知识.

概念:

假设我们现在有一个无向图G=(V,E);

　　割点:我们假设一个点x∈V,如果删去这个点和它相关的所有的边,那么这个无向图(不一定连通)能分成2个或者2个以上互不连通的子图,那么这个点即可以称为割点.

　　桥(割边):就是我们假设有一条边e∈(E),假设删去这条边,我们可以将这个无向图(不一定连通)分成2个或者2个以上互不连通的子图,那么称这条神奇的边为割边或者桥.

　　时间戳:我们随便从无向图中选定一个点作为根(我一般选择节点1),然后我们从这个点开始遍历,也就是建立在深度优先遍历上,记录第一次到达这些点的时间,记为 dfn[x]=time .   let me draw ....

从1开始,记录dfn[1]=1,先到左边的点,发现没有遍历过,于是记录dfn,有遍历过就回溯,再继续下去......直到图中所有点都遍历过为止.

 

搜索树:即深度优先遍历后,如果这个点第一次遍历,就和父节点连一条边,那么这将组成一棵树对吧

 

 

绿绿的边就是组成这个搜索树的边,不多解释.

 

 

　　追溯值:这个概念需要深思一下,刚才我们提出搜索树和时间戳,为了方便简述且我也是这么做,我将时间戳作为每个节点的编号,不影响大局.

关于追溯值的定义,李煜东老师是这么说的:

low[x]定义为以下节点的时间戳的最小值:

　　1.以x为根的子树中的节点的时间戳

　　2.通过一条不在搜索树上的边,能够到达这颗子树的节点的时间戳.

你看我画的图,以2为根的子树的节点有{3,4,5},而1号节点可以通过不在搜索树上的边到5号节点,即通过(1,5)这条边到达这颗子树,所以low[2] = dfn[1] = 1;

根据定义,我们先初始化low[x]=dfn[x]:

若搜索树上x是y的父节点,则low[x] = min(low[x],low[y]) [满足第一定义]

若(x,y)这条边不属于搜索树上的,就令 low[x]=min(low[x],dfn[y]) [满足第二定义]

 

至此我们完成了基本的操作.

 

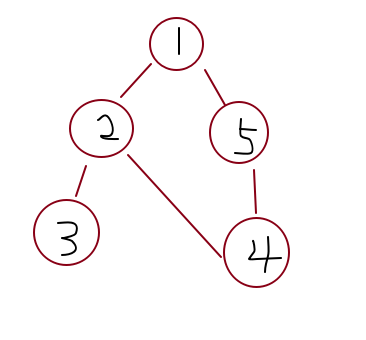
割边判定法则

无向边(x,y)是割边,满足:搜索树上的点x的子节点y,使得: dfn[x] < low[y]

就是y这个点,无法通过其他的边到达比x这个点更早到达的点,也就是说y这个点,除了通过(x,y)这条边外,无法到达以y为根的子树以外的世界,所以当我们断掉这条边的时候,不就是这颗子树处于封闭状态吗?所以它就把这个图分割了嘛

反之,如果不存在dfn[x]<low[y],则说明以y为根的子树除了走(x,y)这条路外,也可以绕道通往外面的世界,那么这条边就限制不到它的自由了,所以(x,y)不是割边.

不难发现(敲黑板),割边一定是搜索树上的边,并且一个简单环里的边一定不是割边.

同时我们也可以发现,因为图是无向的,所以通过x一定是可以找到它的父节点fa对吧,根据low的定义,我们不能用dfn[fa]来更新low[x],因为(fa,x)这条边在搜索树上的

但存在有一种情况:

存在重边,但是(fa,x)在搜索树上,如同上图的(2,3)边,如果出现2条(2,3)边的话,根据low的定义,dfn[2]<low[3]的,但是如果删去此边依旧存在通路,所以此边必不是割边,这就不满足该算法了

那应该怎么办?

法1:直接判断是否能遍历第二次,具体细节交给各位了

法2:如图所示--　　

因为当我们用链式前向星(链表)时,是将无向边拆成有向边存储的,如果我们边从1存起,那么的话,边是成对存在的,如1和2,3和4,5和6等.那么可以用异或1来解决重边问题,即如果从边1到另一个点,2这条边就不能遍历,异或1可以很好的解决这种问题.

inline ll tarjan(ll x,ll e){
    dfn[x]=low[x]=++cnt;
    for(R ll i=head[x];i;i=next[i]){
        ll y=ver[i];
        if(!dfn[y]){
            tarjan(y,i);
            low[x]=min(low[x],low[y]); 
            if(dfn[x]<low[y]){
                b[i]=b[i^1]=1;
            }
        }
        else if(i!=(e^1))
        low[x]=min(low[x],dfn[y]); 
    }
}

割点判定法则:

1.当x不是搜索树上的根的话,y是x的子节点,则x是割点满足条件: dfn[x]<=low[y] [即y这颗树"最远"只可能到x,也就是到不了比x更早遍历的点,那说明y这颗树上的点都被x封锁了嘛]

2.当x是搜索树上的根的话,y是x的子节点,依旧要满足:dfn[x]<=low[y] ,但要起码有2个或者2个以上的y满足此定义式,请深思片刻就可以想到了,没啥问题吧.......

inline void tarjan(ll x){
    low[x]=dfn[x]=++cnt;
    ll f=0;
    for(R ll i=head[x],y;i;i=next[i]){
        y=ver[i];
        if(!dfn[y]){
        tarjan(y);
        low[x]=min(low[x],low[y]);
        if(dfn[x]<=low[y])    {
            f++;
            if(x!=1 || f>1) cut[x]=1;
        }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}
//当然,由于是割点,即断它就把它所有关联边断掉,所以不用考虑父节点和重边的情况,具体的交给你们想了

题目传送门