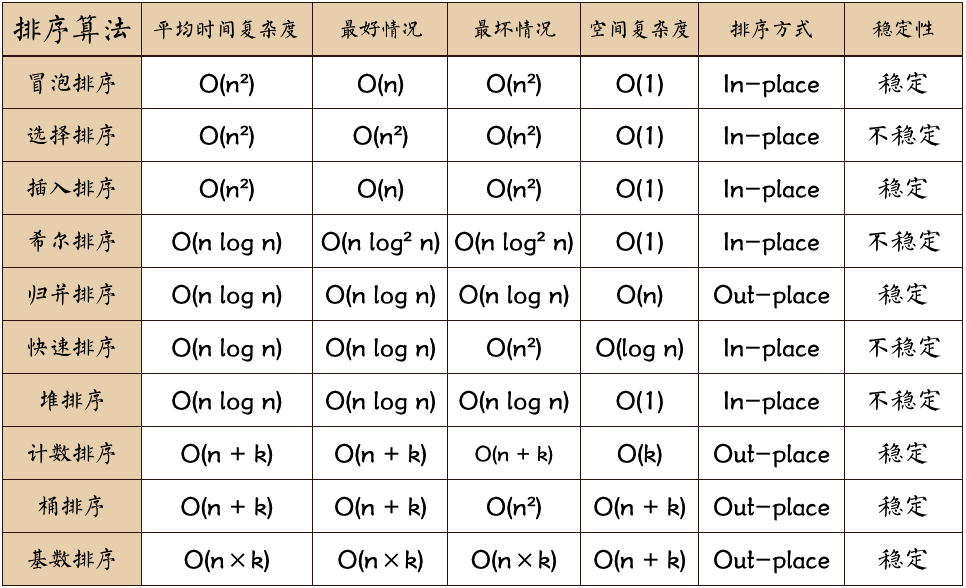
比较排序:
冒泡:两两交换
选择:选择末序列最大(最小)值,同对应位置交换
插入:从后往前扫描有序序列
希尔排序:又叫做缩小增量排序,希尔增量:n/2 n/4 ... 1,O(n^2),Hibbard增量:1,3,7,2hk-1,O(n^1.5);下界为O(nlog(2n))
非比较排序:
桶排序:N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)
即:平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。如果相对于同样的N,桶数量M越大,其效率越高,最好时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价无疑是昂贵的。此外,桶排序是稳定的。
基数排序:n个待排数据,d个关键码,关键码取值范围radix,则时间复杂度:O(d*(n+radix))
总结
冒泡排序是基础,每轮遍历将“最大元素”移至正确位置(“最右边”),不稳定的O(n^2);
选择排序要了解,选择排序每轮遍历将“最小(大)元素”移至正确位置(“最左(右)边”),稳定的O(n^2);
插入排序最简单,适合数据量较小的排序,依然是O(n^2);
希尔排序是插入排序升级版,不好用,为O(nlog^2n);
归并排序和快速排序要熟记原理并会写代码。时间复杂度都是O(nlogn),前者不稳定,后者稳定。最常用的排序方法。
堆排序代码复杂,不太好理解,也不好用,为O(nlogn)。
计数排序、桶排序、基数排序都不是比较排序,可以归为一类,对数据有特殊的要求。其中计数排序是基础,类似建立map对应;桶排序将数据的大小分到不同的桶中,桶内再微小排序;基数排序则是多次的桶排序,每次桶排序根据对应数位将数据分到不同桶中。