OpenCV常用基本处理函数（8）图像变换

傅里叶变换

傅里叶变换在实际中有非常明显的物理意义，设f是一个能量有限的模拟信号，则其傅里叶变换就表示f的频谱。

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。

对于一个正弦信号，如果它的幅度变化非常快，我们可以说他是高频信号，如果变化非常慢，我们称之为低频信号。把这种想法应用到图像中，图像那里的频率变化非常大呢？边界点或者噪声。所以我们说边界和噪声是图像中的高频分量（高频是指灰度变化非常快，而非次数多，也可以说是图像灰度呈阶跃变化的区域）。没有大幅度变化我们称之为低频分量。除颗粒噪音外，图像细节的边缘、轮廓处都是灰度变化突变区域，它们都具有变换后的高频分量特征。

从物理效果看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数。

傅里叶频谱图上我们看到的明暗不一的亮点，其意义是指图像上某一点与邻域点差异的强弱，即梯度的大小，（图像中的低频部分指低梯度的点）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅里叶变换后的频谱图，我们就可以直观地看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的、边界分明且边界两边像素差异较大的。

傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变换 (DFT) 分析图像的频域特性。实现 DFT 的一个快速算法被称为快速傅里叶变换（FFT）。

OpenCV 中相应的傅里叶变换和逆变换的函数是 cv2.dft() 和 cv2.idft()

其中得到结果之后还需要进行一次平移操作，通过np.fft.fftshift()进行平移，

下一步通过频率图构造振频谱（不是很懂）；cv2.magnitude好像是合并两个不同方向的数据，例如x,y方向的梯度来形成整个图形的梯度；

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('messi5.jpg',0)

dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
#构造振频谱
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

HPF（高通滤波）将低频部分去除， LPF（低通滤波）将高频部分去除。其实就是对图像进行模糊操作，比如我们可以使用一个60x60 的矩形窗口（高斯窗口最佳）对图像进行掩模操作从而去除低频分量；

首先需要构建一个掩模，与低频区域对应的地方设置为 1, 与高频区域对应的地方设置为 0。

HPF包括sobal算子和拉普拉斯算子，使用此算子进行操作，达到计算梯度的目的，也可以说是边缘检测；

模板匹配

模板匹配是用来在一副大图中搜寻查找模版图像位置的方法。OpenCV 为我们提供了函数：cv2.matchTemplate()。和 2D 卷积一样，它也是用模板图像在输入图像（大图）上滑动，并在每一个位置对模板图像和与其对应的输入图像的子区域进行比较。

具体匹配算法有多种；

 多对象的模板匹配

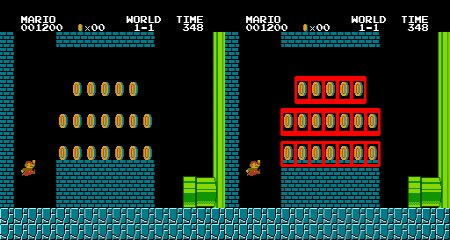
import cv2
import numpy as np
from matplotlib import pyplot as plt

img_rgb = cv2.imread('mario.png')
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
template = cv2.imread('mario_coin.png',0)
w, h = template.shape[::-1]

res = cv2.matchTemplate(img_gray,template,cv2.TM_CCOEFF_NORMED)
threshold = 0.8
loc = np.where( res >= threshold)
for pt in zip(*loc[::-1]):
    cv2.rectangle(img_rgb, pt, (pt[0] + w, pt[1] + h), (0,0,255), 2)

cv2.imwrite('res.png',img_rgb)

效果如图：

霍夫变换

霍夫变换在检测各种形状的的技术中非常流行，如果你要检测的形状可以用数学表达式写出，你就可以是使用霍夫变换检测它。

 参考自:opencv-python中文文档以及博客https://www.cnblogs.com/Undo-self-blog/p/8439279.html