版权声明:本文为博主原创文章,转载请注明出处
机器学习的研究领域是发明计算机算法,把数据转变为智能行为。机器学习和数据挖掘的区别可能是机器学习侧重于执行一个已知的任务,而数据发掘是在大数据中寻找有价值的东西。
机器学习一般步骤
- 收集数据,将数据转化为适合分析的电子数据
- 探索和准备数据,机器学习中许多时间花费在数据探索中,它要学习更多的数据信息,识别它们的微小差异
- 基于数据训练模型,根据你要学习什么的设想,选择你要使用的一种或多种算法
- 评价模型的性能,需要依据一定的检验标准
- 改进模型的性能,有时候需要利用更高级的方法,有时候需要更换模型
机器学习算法
有监督学习算法
用于分类:k近邻,朴素贝叶斯,决策树,规则学习,神经网络,支持向量机
用于数值预测:线性回归,回归树,模型树,神经网络,支持向量机
无监督学习算法
用于模式识别(数据之间联系的紧密性):关联规则
用于聚类:k均值聚类
R语言机器学习算法实现
kNN(k-Nearest Neighbors,k近邻)
- 原理:计算距离,找到测试数据的k个近邻,根据k个近邻的分类预测测试数据的分类
- 应用k近邻需要将各个特征转换为一个标准的范围(归一化处理),可以应用min-max标准化(所有值落在0~1范围,新数据=(原数据-最小值)/(最大值-最小值)),也可以应用z-score 标准化(新数据=(原数据-均值)/标准差)。
- 对于名义变量(表示类别),可以进行哑变量编码,其中1表示一个类别,0表示其它类别,对于n个类别的名义变量,可以用n-1个特征进行哑变量编码,比如(高,中,低),可以用高、中两类的哑变量表示这三类(高:1是,0 其它,中:1是,0,其它)
- 优点:简单且有效,对数据分布没有要求,训练阶段很快;
- 缺点:不产生模型,在发现特征之间的关系上的能力有限,分类阶段很慢,需要大量的内存,名义变量和缺失数据需要额外处理
- R代码:
使用class包的knn函数,对于测试数据中的每一个实例,该函数使用欧氏距离标识k个近邻,然后选出k个近邻中大多数所属的那个类,如果票数相等,测试实例会被随机分配。
dt_pred <- knn(train = dt_train,test = dt_test,class = dt_train_labels,k = 3) #train:一个包含数值型训练数据的数据库;test:一个包含数值型测试数据的数据框;class训练数据每一行分类的一个因子变量;k:标识最近邻数据的一个整数(通常取实例数的平方根); 该函数返回一个向量,该向量含有测试数据框中每一行的预测分类
尽管kNN是并没有进行任何学习的简单算法,但是却能处理及其复杂的任务,比如识别肿瘤细胞的肿块。 - 对R自带iris数据用kNN进行训练、预测并与实际结果对比
llibrary(class)
library(gmodels)
#prepare data
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
iris_z <- as.data.frame(scale(iris_rand[,-5])) #z score normalize
train <- iris_z[1:105,]
test <- iris_z[106:150,]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#kNN
pred <- knn(train,test,train.label,k=10)
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)

这个结果显示kNN对测试数据全部预测正确
朴素贝叶斯分类
- 原理:基于朴素贝叶斯定理,根据先验概率计算预测实例的属于不同类别的总似然,再将某类别的似然除以不同类别似然的和得到预测实例在某类别的概率
- 应用朴素贝叶斯算法每个特征必须是分类变量,对于数值型变量,可以将数值型特征离散化(分段),可以根据直方图查看数据明显的分隔点,如果没有明显的分隔点,可以使用三分位数,四分位数,五分位数,分段太少会把重要信息丢失
- 拉普拉斯估计:对于某些从来没有出现的概率为0的,会影响概率的估计,拉普拉斯估计本质上是在概率表的每个计数加上一个较小的数,这样保证每一类中每个特征发生的概率是非零的。
- 优点:简单、快速、有效;能处理噪声数据和缺失数据;需要用来训练的例子相对较少,但同样能处理好大量的例子;很容易获得一个预测的估计概率值;
- 缺点:依赖于一个常用的错误假设,即一样的重要性和独立特征;应用在大量数值特征的数据集时并不理想;概率的估计值相对于预测的类而言更加不可靠。
- R代码:
使用维也纳理工大学统计系开发的e1071添加包中的naiveBayes
m <- naiveBayes(train,class,laplace=0) #train:数据框或者包含训练数据的矩阵,class:包含训练数据每一行的分类的一个因子向量,laplace:控制拉普拉斯估计的一个数值,可以进行调节看是否会提高模型性能;该函数返回一个朴素贝叶斯模型对象,该对象能够用于预测
p <- predict(m,test,type="class") #m:由函数naiveBays( )训练的一个模型 ,test:数据框或者包含测试数据的矩阵,包含与用来建立分类器的训练数据的相同特征;type:值为"class"或者"raw",标识预测向量最可能的类别值或者原始预测的概率值
library(e1071)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,-5]
test <- iris_rand[106:150,-5]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#tranform numerical variable to classified variable
conver_counts <- function(x){
q <- quantile(x)
sect1 <- which(q[1] <= x & x<= q[2])
sect2 <- which(q[2 ]< x & x <= q[3])
sect3 <- which(q[3]< x & x <= q[4])
sect4 <- which(q[4]< x & x <= q[5])
x[sect1] <- 1
x[sect2] <- 2
x[sect3] <- 3
x[sect4] <- 4
return(x)
}
train <- apply(train,2,conver_counts)
#naiveBayes
m <- naiveBayes(train,train.label,laplace=1)
pred <- predict(m,test,type="class")
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
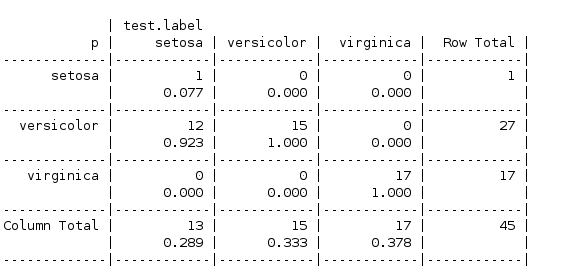
可见对第一类(setosa)分类上预测错误率很高,这可能反映了朴素贝叶斯算法的缺点,对于处理大量数值特征数据集时并不理想
决策树
- 原理:以树形结构建立模型。使用一种称为递归划分的探索法。这种方法通常称为分而治之,因为它利用特征的值将数据分解为具有相似类的较小的子集。从代表整个数据集的数据结点开始,该算法选择最能预测目标类的特征,然后,这些案例将被划分到这一特征的不同值的组中,这一决定形成了第一组树枝。该算法继续分而治之其他结点,每次选择最佳的候选特征,直到达到停止的标准。如果一个节点停止,它可能具有下列情况:节点上所有(几乎所有)的案例都属于同一类,没有剩余的特征来分辩案例之间的区别,决策树已经达到了预先定义的大小限制。
- C5.0算法,时最知名的决策树算法之一,单线程版本的源代码是公开的,R中有编写好的该程序。C5.0算法已经成为生成决策树的行业标准,因为它适用于大多数类型的问题,并且可以直接使用。与其它先进的机器学习模型(神经网络和支持向量机)相比,一般表现的几乎一样,并且更容易理解和部署
- 选择最佳的分割,需要确立分割的标准,有信息增益,基尼系数,卡方统计量,和增益比,C5.0算法使用信息增益
- 修剪决策树:如果决策树增长过大,将会使决策过于具体,模型将会过度拟合训练数据,解决这个问题的一种方法是一旦达到一定数量的决策,或者决策节点仅含有少量的案例,我们就停止树的增长,这叫做提前停止法,或者预剪枝决策树法。分为预剪枝(提前规定树的大小)和后剪枝(一旦树生长的过大,就根据节点处的错误率使用修剪准则将决策树减少到更合适的大小,通常比预剪枝更有效)。
- 自适应增强算法:进行许多次尝试,在决策树中是建立许多决策树,然后这些决策树通过投票表决的方法为每个案例选择最佳的分类。
- 优点:一个适用于大多数问题的通用分类器;高度自动化的学习过程,可以处理数值型数据、名义特征以及缺失数据;只使用最重要的特征;可以用于只有相对较少训练案例的数据或者有相当多训练案例的数据;没有数学背景也可解释一个模型的结果(对于比较小的树);比其他复杂的模型更有效
- 缺点:决策树模型在根据具有大量水平的特征进行划分时往往是有偏的;很容易过度拟合或者不能充分拟合模型;因为依赖于轴平行分割,所以在对一些关系建立模型时会有困难;训练数据中的小变化可能导致决策逻辑的较大的变化;大的决策树可能难以理解,给出的决策可能看起来违反直觉。
- R代码:
使用R包C50的函数C5.0
m <- C5.0(train,class,trials=1,costs=NULL) #train:一个包含训练数据的数据框;class:包含训练数据每一行的分类的一个因子;trials:为一个可选数值,用于控制自适应增强循环的次数(默认值为1),一般用10,因为研究标明,这能降低关于测试数据大约25%的概率;costs:为一个可选矩阵,用于给出与各种类型错误相对应的成本,和混淆矩阵稍微不同,行用来表示预测值,列用来表示实际值);函数返回一个C5.0模型对象,该对象能够用于预测
p <- predict(m,test,type="class") #m:有函数C5.0()训练的一个模型;test:一个包含训练数据的数据框,该数据框和用来创建分类其的数据框有同样的特征;type:取值为"class"或者"prob",表识预测是最可能的类别值或者是原始的预测概率;该函数返回一个向量,根据参数type的取值,该向量含有预测的类别值或者原始预测的概率值
library(C50)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,-5]
test <- iris_rand[106:150,-5]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#C50
m <- C5.0(train,train.label,trials = 10)
pred <- predict(m,test,type="class")
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
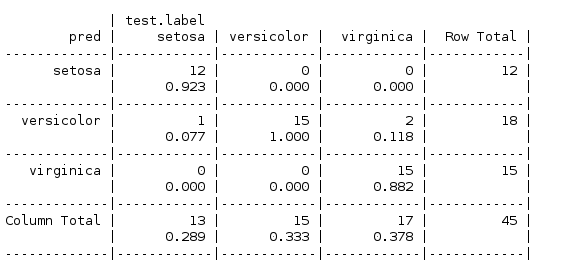
规则学习分类
- 原理:规则学习算法使用了一种称为独立而治之的探索法。这个过程包括确定训练数据中覆盖一个案例子集的规则,然后再从剩余的数据中分离出该分区。随着规则的增加,更多的数据子集会被分离,直到整个数据集都被覆盖,不再有案例残留,独立而治之和决策树的分而治之区别很小,决策树的每个决策节点会受到过去决策历史的影响,而规则学习不存在这样的沿袭。随着规则的增加,更多的数据子集会被分离,知道整个数据集都被覆盖,不再有案例被保留
单规则(1R)算法
- ZeroR,一个规则学习算法,从字面上看没有规则学习,对于一个未标记的案例,不用考虑它的特征值就会把它预测为最常见的类
- 单规则算法(1R或OneR)在ZeroR的基础上添加一个规则。像K近邻一样虽然简单,但是往往表现的比你预期的要好。
- 优点:可以生成一个单一的、易于理解的、人类可读的经验法则(大拇指法则);表现往往出奇的好;可以作为更复杂算法的一个基准;
- 缺点:只使用了一个单一的特征;可能会过于简单
- R代码:
使用R包RWeka中OneR()函数来实现1R算法
m <- OneR(class ~ predictors,data = mydata) #class:是mydata数据框中需要预测的那一列;predictors:为一个公式,用来指定mydata数据框中用来进行预测的特征;data:为包含一个class和predictors所要求的数据的数据框;该函数返回一个1R模型对象,该对象能够用于预测
p <- predict(m,test) #m:由函数OneR()训练的一个模型;test:一个包含测试数据的数据框,该数据框和用来创建分类器的训练数据有着相同的特征;该函数返回一个含有预测的类别的向量
library(RWeka)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,]
test <- iris_rand[106:150,-5]
test.label <- iris_rand[106:150,5]
m <- OneR(Species ~ .,data=train)
pred <- predict(m,test)
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
查看生成的规则,按照Petal的宽度,分成三类,正确分类了105个里面的101个

对于测试数据的混合矩阵如下
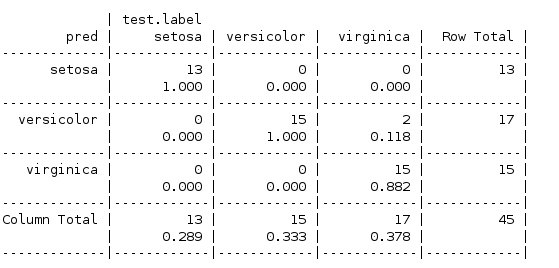
可见只使用了一个规则也能,也做到了不错的效果
RIPPER算法
对于复杂的任务,只考虑单个规则可能过于简单,考虑多个因素的更复杂的规则学习算法可能会有用,但也可能因此会变得更加难以理解。早期的规则学习算法速度慢,并且对于噪声数据往往不准确,后来出现增量减少误差修剪算法(IREP),使用了生成复杂规则的预剪枝和后剪枝方法的组合,并在案例从全部数据集分离之前进行修剪。虽然这提高了性能,但是还是决策树表现的更好。直到1995年出现了重复增量修剪算法(RIPPER),它对IREP算法进行改进后再生成规则,它的性能与决策树相当,甚至超过决策树。
- 原理:可以笼统的理解为一个三步过程:生长,修剪,优化。生长过程利用独立而治之技术,对规则贪婪地添加条件,直到该规则能完全划分出一个数据子集或者没有属性用于分割。与决策树类似,信息增益准则可用于确定下一个分割的属性,当增加一个特指的规则而熵值不再减少时,该规则需要立即修剪。重复第一步和第二步,直到达到一个停止准则,然后,使用各种探索法对整套的规则进行优化。
- 优点:生成易于理解的、人类可读的规则;对大数据集和噪声数据有效;通常比决策树产生的模型更简单
- 缺点:可能会导致违反常理或这专家知识的规则;处理数值型数据可能不太理想;性能有可能不如复杂的模型
- R代码:
使用R包RWeka中JRip()函数,是基于Java实现的RIPPER规则学习算法
m<JRip(class ~ predictors,data = my data) #class:是mydata数据框中需要预测的那一列;predictors:为一个R公式,用来指定mydata数据框中用来进行预测的特征;data:为包含class和predictors所要求的数据的数据框;该函数返回一个RIPPER模型对象,该对象能够用于预测。
p <- predict(m , test) #m:由函数JRip()训练的一个模型;test:一个包含测试数据的数据框,该数据框和用来创建分类器的训练数据有同样的特征;该函数返回一个含有预测的类别值的向量。
library(RWeka)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,]
test <- iris_rand[106:150,-5]
test.label <- iris_rand[106:150,5]
m <- JRip(Species ~ .,data=train)
pred <- predict(m,test)
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)

这次使用了三个规则,(Petal.Width >= 1.8为virginica ,Petal.Length >= 3为versicolor,其它为setosa
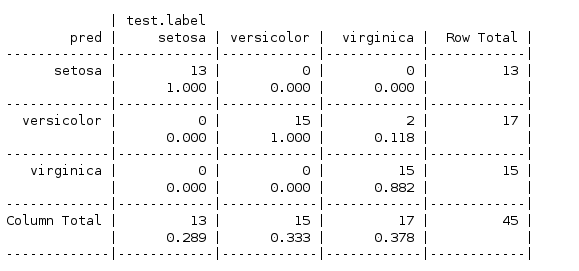
可见虽然增加了规则但是并没有提高模型的性能
预测数值型数据
线性回归
回归主要关注一个唯一的因变量(需要预测的值)和一个或多个数值型自变量之间的关系。
- 如果只有一个自变量,称为一元线性回归或者简单线性回归,否则,称为多元回归。
- 原理:对线性参数的估计使用最小二乘估计
- 广义线性回归:它们对线性模型进行了两方面的推广:通过设定一个连接函数,将响应变量的期望与线性变量相联系,以及对误差的分布给出一个误差函数。这些推广允许许多线性的方法能够被用于一般的问题。比如逻辑回归可以用来对二元分类的结果建模;而泊松回归可以对整型的计数数据进行建模。
- 优点:迄今为止,它是数值型数据建模最常用的方法;可适用于几乎所有的数据;提供了特征(变量)之间关系的强度和大小的估计
- 缺点:对数据作出了很强的假设;该模型的形式必须由使用者事先指定;不能很好地处理缺失数据;只能处理数值特征,所以分类数据需要额外的处理;需要一些统计学知识来理解模型。
- LASSO回归算法:LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选(只选择对因变量有显著影响的自变量)和复杂度调整(通过参数控制模型复杂度,避免过度拟合)。它通过惩罚最大似然来拟合广义线性模型,正则化路径是通过正则化参数lambda的值的网格上计算lasso或者弹性网络惩戒,lambda越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型。
- R代码:
使用R包glmnet中glmnet()函数拟合LASSO回归模型
glmnet(x, y, family=c("gaussian","binomial","poisson","multinomial","cox","mgaussian"),
weights, offset=NULL, alpha = 1, nlambda = 100,
lambda.min.ratio = ifelse(nobs<nvars,0.01,0.0001), lambda=NULL,
standardize = TRUE, intercept=TRUE, thresh = 1e-07, dfmax = nvars + 1,
pmax = min(dfmax * 2+20, nvars), exclude, penalty.factor = rep(1, nvars),
lower.limits=-Inf, upper.limits=Inf, maxit=100000,
type.gaussian=ifelse(nvars<500,"covariance","naive"),
type.logistic=c("Newton","modified.Newton"),
standardize.response=FALSE, type.multinomial=c("ungrouped","grouped"))
x: 输入矩阵,每列表示变量(特征),每行表示一个观察向量,也支持输入稀疏矩阵(Matrix中的稀疏矩阵类);
y: 反应变量,对于gaussian或者poisson分布族,是相应的量;对于binomial分布族,要求是两水平的因子,或者两列的矩阵,第一列是计数或者是比例,第二列是靶向分类;对于因子来说,最后的水平是按照字母表排序的分类;对于multinomial分布族,能有超过两水平的因子。无论binomial或者是multinomial,如果y是向量的话,会强制转化为因子。对于cox分布族,y要求是两列,分别是time和status,后者是二进制变两,1表示死亡,0表示截尾,survival包带的Surv()函数可以产生这样的矩阵。对于mgaussian分布族,y是量化的反应变量的矩阵;
family: 反应类型,参数family规定了回归模型的类型:family="gaussian"适用于一维连续因变量(univariate)family="mgaussian",适用于多维连续因变量(multivariate),family="poisson"适用于非负次数因变量(count),family="binomial"适用于二元离散因变量(binary),family="multinomial"适用于多元离散因变量(category)
weights: 权重,观察的权重。如果反应变量是比例矩阵的话,权重是总计数;默认每个观察权重都是1;
offset: 包含在线性预测中的和观察向量同样长度的向量,在poisson分布族中使用(比如log后的暴露时间),或者是对于已经拟合的模型的重新定义(将旧模型的因变量作为向量放入offset中)。默认是NULL,如果提供了值,该值也必须提供给predict函数;
alpha: 弹性网络混合参数,0 <= a <=1,惩罚定义为(1-α)/2||β||_2^2+α||β||_1.其中alpha等于1是lasso惩罚,alpha等于0是ridge(岭回归)的惩罚;
nlambda:lambda值个数;拟合出n个系数不同的模型
lambda.min.ratio:lambda的最小值,lambda.max的比例形式,比如全部系数都是0的时候的最小值。默认值依赖于观察的个数和特征的个数,如果观察个数大于特征个数,默认值是0.0001,接近0,如果观察个数小于特征个数,默认值是0.01。在观察值个数小于特征个数的情况下,非常小的lambda.min.ratio会导致过拟合,在binominal和multinomial分布族性,这个值未定义,如果解释变异百分比总是1的话程序会自动退出;
lambda:用户提供的lambda序列。一个典型的用法基于nlambada和lambda.min.ratio来计算自身lambda序列。如果提供lambda序列,提供的lambda序列会覆盖这个。需谨慎使用,不要提供单个值给lambda(对于CV步骤后的预测,应使用predict()函数替代)。glmnet依赖于缓慢开始,并且它用于拟合全路径比计算单个拟合更快;
standardize:对于x变量是否标准化的逻辑标志,倾向于拟合模型序列。 系数总是在原有规模返回,默认standardize=TRUE。如果变量已经是同一单位,你可能并不能得到想要的标准化结果。
intercept:是否拟合截距,默认TRUE,或者设置为0(FALSE)
thresh:坐标下降的收敛域值,每个内部坐标下降一直进行循环,直到系数更新后的最大改变值比thresh值乘以默认变异要小,默认thresh为1E-7;
dfmax:在模型中的最大变量数,对于大量的变量数的模型但我们只需要部分变量时可以起到作用;
pmax:限制非零变量的最大数目;
exclude:要从模型中排除的变量的索引,等同于一个无限的惩罚因子;
penalty.factor:惩罚因子,分开的惩罚因子能够应用到每一个系数。这是一个数字,乘以lambda来允许不同的收缩。对于一些变量来说可以是0,意味着无收缩,默认对全部变量是1,对于列在exlude里面的变量是无限大。注意:惩罚因子是内部对nvars(n个变量)的和进行重新调整,并且lambda序列将会影响这个改变;
lower.limits:对于每个系数的更低限制的向量,默认是无穷小。向量的每个值须非正值。也可以以单个值呈现(将会重复),或者是(nvars长度);
upper.limit:对于每个系数的更高限制的向量,默认是无穷大;
maxit:所有lambda值的数据最大传递数;
type.gaussian:支持高斯分布族的两种算法类型,默认nvar < 500使用"covariance“,并且保留所有内部计算的结果。这种方式比"naive"快,"naive"通过对nobs(n个观察)进行循环,每次内部计算一个结果,对于nvar >> nobs或者nvar > 500的情况下,后者往往更高效;
type.logistic:如果是"Newton“,会使用准确的hessian矩阵(默认),当用的是"modified.Newton“时,只使用hession矩阵的上界,会更快;
standardize.response:这个参数时对于"mgaussian“分布族来说的,允许用户标准化应答变量;
type.multinomial:如果是"grouped",在多项式系数的变量使用分布lasso惩罚,这样能确保它们完全在一起,默认是"ungrouped"。
glmnet返回S3类,"glmnet","*","*"可以是elnet,lognet,multnet,fishnet(poisson),merlnet
call:产生这个对象的调用;
a0:截距;
beta:对于elnet, lognet, fishnet和coxnet模型,返回稀疏矩阵格式的系数矩阵(CsparseMatrix),对于multnet和mgaussian模型,返回列表,包括每一类的矩阵;
lambda:使用的lambda值的实际序列;当alpha=0时,最大的lambda值并不单单等于0系数(原则上labda等于无穷大),相反使用alpha=0.01的lambda,由此导出lambda值;
dev.ratio:表示由模型解释的变异的百分比(对于elnet,使用R-sqare)。如果存在权重,变异计算会加入权重,变异定义为2x(loglike_sat-loglike),loglike_sat是饱和模型(每个观察值具有自由参数的模型)的log似然。因此dev.ratio=1-dev/nulldev;越接近1说明模型的表现越好
nulldev:NULL变异(每个观察值),这个定义为2*(loglike_sat-loglike(Null));NULL模型是指截距模型,除了Cox(0 模型);
df:对于每个lambda的非零系数的数量。对于multnet这是对于一些类的变量数目;
dfmat:仅适用于multnet和mrelnet。一个包括每一类的非零向量数目的矩阵;
dim:系数矩阵的维度;
nobs:观察的数量;
npasses:全部lambda值加和的数据的总的通量;
offset:逻辑变量,显示模型中是否包含偏移;
jerr:错误标记,用来警告和报错(很大部分用于内部调试验)
而直接显示的结果有三列,分别是df,%Dev (就是dev.ratio),lambda是每个模型对应的λ值
predict(object,newx,s=NULL,type=c("link","reponse","coefficients","nonzero","class"),exact=FALSE,offset,...)
coef(object,s=NULL,exact=FALSE)
object:glmnet返回的对象;
newx:用来预测的矩阵,也可以是系数矩阵;这个参数不能用于type=c(""coefficents","nonzero");
s:惩罚参数lambda的值,默认是用来创建模型的全部lambda值;
type:预测值的类型;"link”类型给"binomial",“multinomial","poisson"或者"cov"模型线性预测的值,对于"gaussian”模型给拟合值。"response"类型,对于"binominal“和"multinomial”给拟合的概率,对于"poisson“,给拟合的均值,对于"cox",给拟合的相对未及;对于"gaussion",response等同于"link“类型。"coefficients"类型对于需求的s值计算系数。注意,对于"binomial”模型来说,结果仅仅对因子应答的第二个水平的类返回。“class"类型仅仅应用于"binomial”和"multinomial“模型,返回最大可能性的分类标签。"nonzero”类型对每个s中的值返回一个列表,其中包含非0参数的索引;
exact:这个参数仅仅对于用于预测的s(lambda)值不同于原始模型的拟合的值时,这个参数起到作用。如果exact=FALSE(默认),预测函数使用线性解释来对给的s(lambda)值进行预测。这时一个非常接近的结果,只是稍微有点粗糙。如果exact=TRUE,这些不同的s值和拟合对象的lambda值进行sorted和merged,在作出预测之前进行模型的重新拟合。在这种情况下,强烈建议提供原始的数据x=和y=作为额外的命名参数给perdict()或者coef(),predict.glmnet()需要升级模型,并且期望用于创建接近它的数据。尽管不提供这些额外的参数它也会运行的很好,在调用函数中使用嵌套序列很可能会中断。
offset:如果使用offset参数来拟合,必须提供一个offset参数来作预测。除了类型"coefficients"或者"nonzero“
...:可以提供参数其它参数的机制,比如x=when exact=TRUE,seeexact参数。
library(glmnet )
library(psych)
#dummy variable encoding
iris$issetosa <- ifelse(iris$Species=="setosa",1,0)
iris$isversicolor <- ifelse(iris$Species=="versicolor",1,0)
iris_dt <- iris[,-5]
pairs.panels(iris_dt) #scatterplot matrix
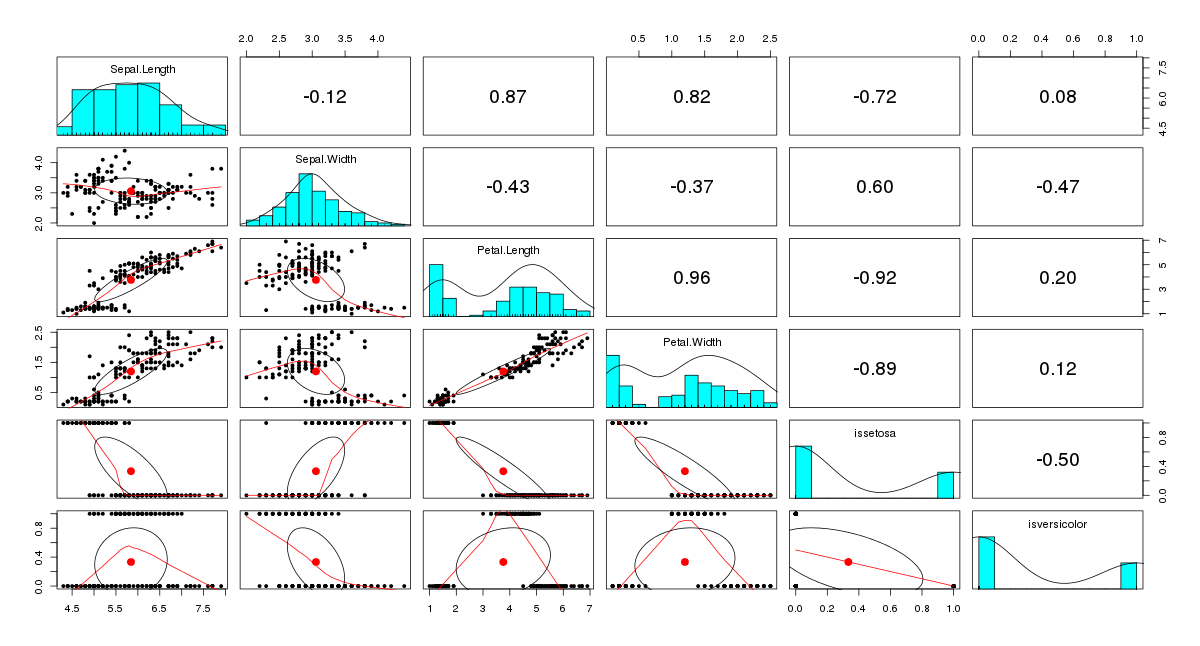
pairs.panel画出散点图矩阵,对角线上方显示的是变量之间的相关系数,每个散点图中呈椭圆形的对象称为相关椭圆,它提供一种变量之间是如何密切相关的可视化信息。位于椭圆中间的的点表示x轴变量和y轴变量的均值所确定的点。两个变量之间的相关性由椭圆的形状表示,椭圆越被拉伸,其相关性就越强。散点图中绘制的曲线称为局部回归平滑,它表示x轴和y轴变量之间的一般关系。iris数据画出的散点图矩阵中的相关系数和散点图曲线都可见Petal.Length和Petal.Width有着强的相关性,而从散点图曲线也可看出,似乎Sepal.Length超出一定阈值后,Sepal.Length增加,Petal.Length也增加,并且也和品种是setosa或者versicolor也有关系。以Petal.Width作为因变量作线性回归。
library(glmnet )
#dummy variable encoding
iris$issetosa <- ifelse(iris$Species=="setosa",1,0)
iris$isversicolor <- ifelse(iris$Species=="versicolor",1,0)
#divided into training sets and test sets
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,-c(4,5)]
test <- iris_rand[106:150,-c(4,5)]
train_value <- iris_rand[1:105,4]
test_value <- iris_rand[106:150,4]
#lasso
m_lasso <- glmnet(as.matrix(train),train_value,family = "gaussian")
plot(data.frame(df=m_lasso$df,dev.ratio=m_lasso$dev.ratio),type="b",cex=0.6)
coef(m_lasso, s=0.0497000) #min df
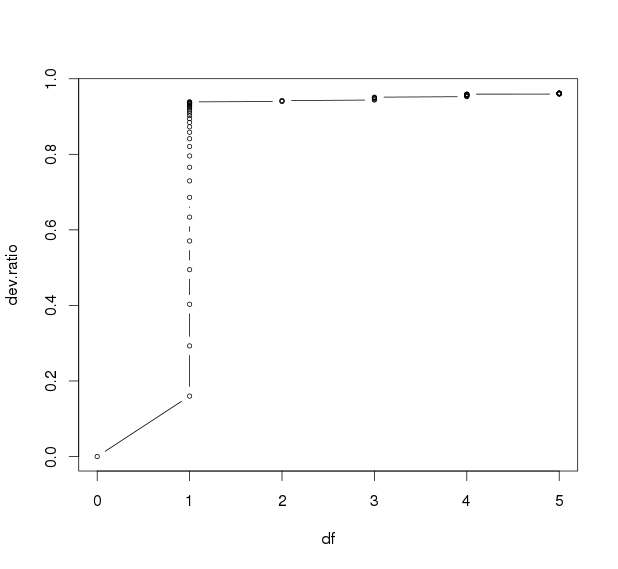

查看变量个数与模型解释变异百分比的点图,发现在df=1时已经开始平缓,已经可以解释93%的变异。因此取df=1的可以解释最大变异的lambda,0.0452800,查看系数发现使用了两个特征,其中一个系数非常低,并不是我们需要的,因此lambda改为第二个解释最大变异的lambda,0.0497000.
用coef取出参数如下
lambda=0.0452800
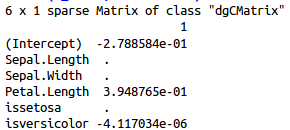
lambda=0.0497000
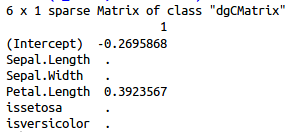
用选出的lambda值进行预测
pred <- predict(m_lasso,newx=as.matrix(test),s=0.0497000)
summary(pred)
summary(test_value)
cor(test_value,pred)
MAE <- mean(abs(pred - test_value))
mean(abs(mean(train_value) - test_value))
发现预测值和真实值范围非常接近
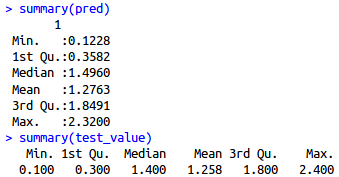
相关系数高
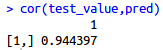
MAE(平均绝对误差,反映预测值和真实值的差距)仅为0.1981803,如果只是拿训练集的均值预测的话,MAE高达0.6551746)

综合以上的度量标准,说明我们的模型预测的不错。
回归树和模型树
- 决策树用于数值预测分为两类,第一类称为回归树,第二类称为模型树。
- 回归树作为分类回归树的一部分引入,回归树并没有使用线性回归的办法,而是基于到达节点的案例的平均值进行预测。
- 模型树,比回归树晚几年引入,但是或许功能更加强大。模型树和回归树以大致相同的方式生长,但是在每个叶节点,根据到达该节点的案例建立多元线性回归模型。根据叶节点的数目,一棵模型树可能会建立几十个甚至几百个这样的模型,这可能会使模型树更加难以理解,但好处是它们也许能建立一个更加精确的模型。
- 优点:将决策树的优点与数值型数据建立模型的能力相结合;能自动选择特征,允许该方法和大量特征一起使用;不需要使用者事先指定模型;拟合某些类型的数据可能会比线性回归好得多;不要求用统计的知识来解释模型。
- 缺点:不像线性回归那样常用;需要大量的训练数据;难以确定单个特征对于结果的总体净影响;可能比回归模型更难解释。
- 原理:用于数值预测的决策树的建立方式与用于分类的决策树的建立方式大致相同。从根节点开始,按照特征使用分而治之的策略对数据进行划分,在进行一次分割后,将会导致数据最大化的均匀增长。而在分类决策树中,一致性(均匀性)是由熵值来度量的,而对于数值型的数据是未定义的,对于数值型决策树,一致性可以通过统计量(比如方差、标准差或者平均绝对偏差)来度量。不同的决策树生长算法,一致性度量可能会有所不同,但原理是基本相同的。
- 一种常见的分割标准是标准偏差减少,就是原始值的标准差减去分割后不同类的数据加权后的标准差,这里的加权就是该类的数目比上总的数目。决策树停止生长后,假如一个案例使用特征B进行分割,落入某一组B1中,那么该案例的预测值将取B1组的平均值。模型树要多走一步,使用落入B1组的训练案例和落入B2组的训练案例,建立一个相对于其它特征(特征A)的线性回归模型。
- R代码:
在R包rpart(递归划分)中提供了像CART(分类回归树)团队中所描述的最可靠的回归树的实现,
m.rpart <- rpart(dv ~ iv, data = mydata) #dv 是mydata 数据框中需要建模的因变量;iv 为一个R公式,用来指定mydata数据框中的自变量;data:为包含变量dv和变量iv的数据框
p <- predict(m,test,type=c("vector", "prob", "class", "matrix")) #m是有函数rpart训练的一个模型;test一个包含测试数据的数据框,该数据框和用来建立模型的数据具有相同的特征;type:给定返回的预测值的类型,prob返回预测的概率。matrix返回矩阵的形式包括各类的概率。class返回树的分类。否则返回一个向量的结果。
可以使用R包rpart.plot中rpart.plot函数对回归树结果可视化。
目前模型树中最先进的算法是M5'算法,可以通过R包Rweka中M5P函数实现;
m <- M5P(dv ~ iv, data = mydata) #dv 是mydata 数据框中需要建模的因变量;iv 为一个R公式,用来指定mydata数据框中的自变量;data:为包含变量dv和变量iv的数据框
p <- predict(m,test) #m是有函数rpart训练的一个模型;test一个包含测试数据的数据框,该数据框和用来建立模型的数据具有相同的特征
library(rpart)
library(RWeka)
library(rpart.plot)
#dummy variable encoding
iris$issetosa <- ifelse(iris$Species=="setosa",1,0)
iris$isversicolor <- ifelse(iris$Species=="versicolor",1,0)
#divided into training sets and test sets
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train_dt <- iris_rand[1:105,-5]
test <- iris_rand[106:150,-c(4,5)]
test_value <- iris_rand[106:150,4]
#rpart
m.rpart <- rpart(Petal.Width ~ Sepal.Length+Sepal.Width+Petal.Length+issetosa+isversicolor,data = train_dt)
summary(m.rpart)
rpart.plot(m.rpart)
pred <- predict(m.rpart,test)
cor(test_value,pred)
mean(abs(pred - test_value)) #rpart MAE
mean(abs(mean(train_dt$Petal.Width) - test_value)) #mean MAE
#M5P
m.M5P <- M5P(Petal.Width ~ Sepal.Length+Sepal.Width+Petal.Length+issetosa+isversicolor,data = train_dt)
summary(m.M5P)
pred <- predict(m.M5P,test)
cor(test_value,pred)
mean(abs(pred - test_value)) #rpart MAE
mean(abs(mean(train_dt$Petal.Width) - test_value)) #mean MAE
回归树的结果如下

rpart.plot结果
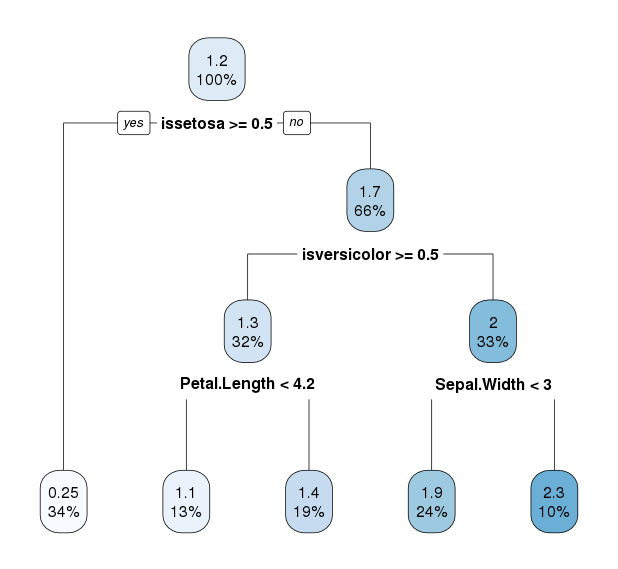
相关性到达0.9797762,回归树(MAF0.1242998)明显比直接用均值预测(MAF0.7255238)更接近于真实的Petal.Width
模型树的结果如下

相关系数到达0.9714331,MAF0.1410668,在这个模型树中,只有一个根节点,相应建立了一个线性模型,直接用Sepal.Length ,Sepal.Width ,Petal.Length三个特征进行预测,和lasso回归模型一样,特征前面的系数代表该特征对Petal.Width的静影响,注意,这里的净影响是指在当前节点这个线性模型中的净影响,在这个线性模型中,每增加一点Sepal.Width和Petal.Length,Petal.Width都会增加,而系数小于0的Sepal.Length ,意味着每增加一点Sepal.Length,Petal.Width就会减少。从结果可以看出,在这个案例中,模型树没有回归树的效果好。
此处模型树在没有生成多个树节点的情况下,只是对特征做了线性回归,MAF达到0.1410668,和之前对数据作线性回归的lasso模型结果(MAF0.1981803)相比,貌似做的更好,但其实之前的lasso回归模型我们限制了特征值个数来避免过拟合,如果增加特征值数量和调整labda参数,一样可以达到比较小的MAF。
小结
本文主要讲了机器学习的一些基本概念,还有部分机器学习方法的基本原理及R语言实现。包括用于分类的机器学习方法:k近邻,朴素贝叶斯,决策树,规则学习;用于数值预测的机器学习方法:lasso回归,回归树,模型树,它们都属于监督学习。下篇文章会说到监督学习中的神经网络和支持向量机,还有其他非监督学习的一些方法。
本文可以作为一个速查和简单的入门,一些函数只列举了部分重要的参数,具体的使用参数可以通过查看R里面的帮助获得。另外如果要用于实践,还需要了解一些K折交叉检验,kappa统计量,ROC曲线内容,以对模型的性能进行评价和对不同的模型进行对比。
参考资料
Brett Lantz:机器学习与R语言
薛毅,陈立萍: 统计建模与R软件(下册)
侯澄钧:热门数据挖掘模型应用入门(一): LASSO : https://cosx.org/2016/10/data-mining-1-lasso
slade_sha的博客 Lasso算法理论介绍 :http://blog.csdn.net/slade_sha/article/details/53164905