LeetCode: Candy

Title:

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

• Each child must have at least one candy.
• Children with a higher rating get more candies than their neighbors.

What is the minimum candies you must give?

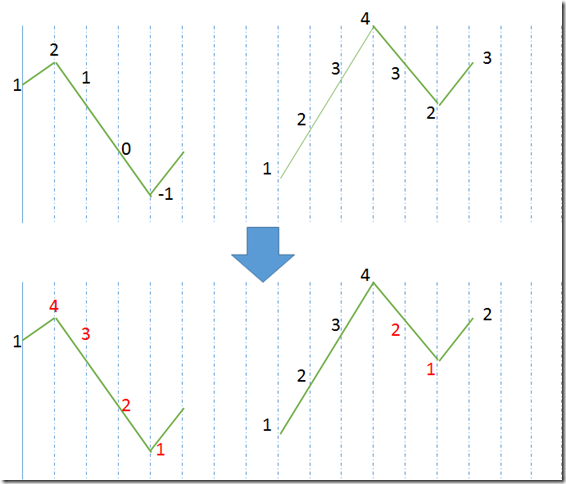
思路(1): 1 4 3 2 1 对于这样的等级，我的想法是依次加，前两个是1,2，但是到3的时候就是1，不过与后面的2,1就会冲突，所以就需要向前调整，将4对应的改为4. 不过这个调整的我们可以发现是针对递减序列的，所以我就想到其实我们可以每次找到一个波谷，波谷的峰值可以由两边决定。另外，权值相等的时候，如2,4,4，第二个4的权重完全可以是1，由题目的最后一句得到。

class Solution {
public:
    int candy(vector<int>& ratings) {
        int s_val = 1;
        int sum = 0;
        for (int i = 0; i < ratings.size(); ){
            int s_idx = i;
            while (i < ratings.size()-1 && ratings[i] < ratings[i+1]){ //递增
                sum += (s_val + i - s_idx);
                i++;
            }
            int m_idx = i;
            while (i < ratings.size()-1 && ratings[i] > ratings[i+1]){//递减
                sum += (i - m_idx + 1);
                i++;
            }
            int m_val = max(s_val+(m_idx-s_idx),i-m_idx+1); //设定波峰值
            
            sum += m_val;
            if (i < ratings.size()-1 && ratings[i] == ratings[i+1])//对于权值相等的处理
                s_val = 1;
            else
                s_val = 2;
            i++;
        }
        return sum;
    }
};

思路（2）首先我们会给每个小朋友一颗糖果，然后从左到右，假设第i个小孩的等级比第i - 1个小孩高，那么第i的小孩的糖果数量就是第i - 1个小孩糖果数量在加一。再我们从右到左，如果第i个小孩的等级大于第i + 1个小孩的，同时第i个小孩此时的糖果数量小于第i + 1的小孩，那么第i个小孩的糖果数量就是第i + 1个小孩的糖果数量加一。

class Solution {
public:
    int candy(vector<int>& ratings) {
        int sum = 0;
        vector<int> v(ratings.size(),1);
        for (int i = 1; i < ratings.size(); i++){
            if (ratings[i] > ratings[i-1])
                v[i] = v[i-1] + 1;
        }
        sum += v[ratings.size()-1];
        for (int i = ratings.size()-2; i >= 0; i--){
            if (ratings[i] > ratings[i+1] && v[i] <= v[i+1]){
                v[i] = v[i+1]+1;
            }
            sum += v[i];
        }
        return sum;
    }
};