3.13 模拟赛

T1 words

题目大意： bzoj 4567

题解链接

考试代码：

（如果不重建树的话会出锅 例子：

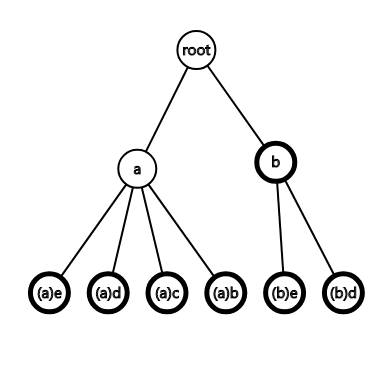
其中加粗的边为有$end$标记的节点，若不重建树，则左边$a$的$sz$为4，右边为3会先走右边

实际上应该先走左边（man太惨了。

T2 tree

题目大意：bzoj 4817

一棵树 支持三种操作：

1 x：把点x到根节点的路径上所有的点染上一种没有用过的新颜色

2 x y：求x到y的路径的权值

3 x：在以x为根的子树中选择一个点，使得这个点到根节点的路径权值最大，求最大权值

思路：

（之前看wls做过这道题，对大致思路有一个了解，当时感觉好神啊

维护每个点到根的路径的权值

这样两个询问的答案分别为$val_a+val_b-2*val_{lca}+1$与子树中的最大值，用线段树可以很方便的维护

对于修改，发现这个过程与$LCT$的$access$很像

使用$LCT$来维护修改，即对于修改，$access$该点，并在过程中修改

找到两个部分内最浅的点，然后用线段树一个$+1$一个$-1$修改即可非常完美的解决

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define ll long long
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define MAXN 100100
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,fst[MAXN],nxt[MAXN<<1],to[MAXN<<1],cnt,dep[MAXN];
int fa[MAXN],sz[MAXN],hvs[MAXN],tot,bl[MAXN],in[MAXN];
int mx[MAXN<<2],tag[MAXN<<2];
void add(int u,int v) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
void dfs(int x,int pa)
{
    fa[x]=pa,sz[x]=1;
    ren if(to[i]^pa) dep[to[i]]=dep[x]+1,dfs(to[i],x),
        sz[x]+=sz[to[i]],hvs[x]=sz[to[i]]>sz[hvs[x]]?to[i]:hvs[x];
}
void Dfs(int x,int anc)
{
    bl[x]=anc,in[x]=++tot;if(!hvs[x]) return ;
    Dfs(hvs[x],anc);ren if(to[i]^fa[x]&&to[i]^hvs[x]) Dfs(to[i],to[i]);
}
int lca(int a,int b)
{
    for(;bl[a]!=bl[b];a=fa[bl[a]])
        if(dep[bl[a]]<dep[bl[b]]) swap(a,b);
    return in[a]<in[b]?a:b;
}
void pshd(int k)
{
    mx[k<<1]+=tag[k],mx[k<<1|1]+=tag[k];
    tag[k<<1]+=tag[k],tag[k<<1|1]+=tag[k],tag[k]=0;
}
void mdf(int k,int l,int r,int a,int b,int x)
{
    if(l==a&&r==b) {tag[k]+=x,mx[k]+=x;return ;}int mid=l+r>>1;
    if(tag[k]) pshd(k);
    if(b<=mid) mdf(k<<1,l,mid,a,b,x);
    else if(a>mid) mdf(k<<1|1,mid+1,r,a,b,x);
    else {mdf(k<<1,l,mid,a,mid,x);mdf(k<<1|1,mid+1,r,mid+1,b,x);}
    mx[k]=max(mx[k<<1],mx[k<<1|1]);
}
int query(int k,int l,int r,int a,int b)
{
    if(l==a&&r==b) return mx[k];int mid=l+r>>1;
    if(tag[k]) pshd(k);
    if(b<=mid) return query(k<<1,l,mid,a,b);
    else if(a>mid) return query(k<<1|1,mid+1,r,a,b);
    else return max(query(k<<1,l,mid,a,mid),query(k<<1|1,mid+1,r,mid+1,b));
}
namespace lct
{
    int ch[MAXN][2],tag[MAXN],fa[MAXN];
    int which(int x) {return ch[fa[x]][1]==x;}
    int isroot(int x) {return ch[fa[x]][1]!=x&&ch[fa[x]][0]!=x;}
    void rotate(int x)
    {
        int f=fa[x],ff=fa[f],k=which(x);
        if(!isroot(f)) ch[ff][ch[ff][1]==f]=x;fa[x]=ff;
        ch[f][k]=ch[x][k^1],fa[ch[x][k^1]]=f,ch[x][k^1]=f,fa[f]=x;
    }
    void splay(int x)
    {
        for(int f;!isroot(x);rotate(x))
            if(!isroot(f=fa[x])) rotate(which(x)==which(f)?f:x);
    }
    int find(int x) {while(ch[x][0]) x=ch[x][0];return x;}
    void access(int x)
    {
        for(int t=0,tmp;x;t=x,x=fa[x])
        {
            splay(x);
            if(ch[x][1]){tmp=find(ch[x][1]);mdf(1,1,n,in[tmp],in[tmp]+sz[tmp]-1,1);}
            ch[x][1]=t;if(t){tmp=find(t);mdf(1,1,n,in[tmp],in[tmp]+sz[tmp]-1,-1);}
        }
    }
};
int main()
{
    n=read(),m=read();int a,b,c;rep(i,2,n) a=read(),b=read(),add(a,b),add(b,a);
    dep[1]=1;dfs(1,0);Dfs(1,1);rep(i,1,n) mdf(1,1,n,in[i],in[i],dep[i]),lct::fa[i]=fa[i];
    while(m--)
    {
        c=read(),a=read();
        if(c==1) lct::access(a);
        else if(c==2)
        {
            b=read(),c=lca(a,b);
            printf("%d
",query(1,1,n,in[a],in[a])+query(1,1,n,in[b],in[b])-2*query(1,1,n,in[c],in[c])+1);
        }
        else printf("%d
",query(1,1,n,in[a],in[a]+sz[a]-1));
    }
}

T3 coin

题目大意：bzoj 4830

两个人分别抛$a$次和$b$次硬币，$a geq b$

求扔$a$次正面总数大于$b$次正面总数的总方案数

思路：

考试时候得了30分 即$sumlimits_{i=1}^a  sumlimits_{j=1}^{min(j,b-1)} C_a^i * C_b^j$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define ll long long
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define MAXN 600100
int MOD;
#define pls(a,b) (a+b)%MOD
#define mul(a,b) ((1LL*a)%MOD*b)%MOD
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,k;
struct P30
{
    int c[1100][1100],ans,t1;
    P30(){memset(c,0,sizeof(c));ans=t1=0;}
    void pre()
    {
        c[0][0]=1;
        rep(i,1,n) {c[i][0]=1;rep(j,1,i) c[i][j]=pls(c[i-1][j],c[i-1][j-1]);}
    }
    void work()
    {
        MOD=(int)pow(10,k);pre();ans=t1=0;
        rep(i,1,n) t1=pls(c[m][i-1],t1),ans=pls(mul(t1,c[n][i]),ans);
        if(k==1) printf("%01d
",ans);
        if(k==2) printf("%02d
",ans);
        if(k==3) printf("%03d
",ans);
        if(k==4) printf("%04d
",ans);
        if(k==5) printf("%05d
",ans);
        if(k==6) printf("%06d
",ans);
        if(k==7) printf("%07d
",ans);
        if(k==8) printf("%08d
",ans);
        if(k==9) printf("%09d
",ans);
    }
}p30;
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        m=read(),k=read();
        if(max(n,m)<=1000) p30.work();
    }
}

前置知识：范德蒙德卷积即$sumlimits_{i=0}^k C_n^i * C_m^{k-i} =C_{n+m}^k$，可以通过其意义简单证明

首先考虑$a=b$的情况，发现对于两人得分不同的情况，将整个序列取反后胜负情况都会发生变化

那么答案即为全集减去得分相同的情况再除以二即$frac{2^{2a}-C_{2a}^a}{2}$

对于$a>b$的情况 发现会存在取反之后A的得分依然高于B的情况，设B原本得分为$i$,A比B多得分为$j$

其余情况仍然满足原来B赢的情况取反后为A赢

对于特殊情况 则有$a-i-j>b-i$即$j<a-b$ 与题目中$a-b leq 10000$的条件符合

设$S$表示特殊情况 则答案为$frac{2^{2a}+S}{2}$

$$S=sumlimits_{i=0}^b sumlimits_j^{a-b-1} C_b^i C_a^{i+j}=sumlimits_{i=0}^b sumlimits_j^{a-b-1} C_b^{b-i} C_a^{i+j}=sumlimits_{i=0}^{a-b-1} C_{a+b}^{b+i}$$

然后就可以使用拓展$lucas$来求解了

但此题卡常 有很多东西需要注意：

由于只有两个质因数，可以预处理阶乘；以及组合数只需要求一半

除以2的东西需要讨论，对$2^k$少乘一个$2$,对$5^k$乘以个$2$的逆元

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<map>
#include<set>
#define ll long long
#define db double
#define inf 2139062143
#define MAXN 2001000
#define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i)
#define lrep(i,s,t) for(register ll i=(s),i##__end=(t);i<=i##__end;++i)
#define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i)
#define ren for(register int i=fst[x];i;i=nxt[i])
#define pb(i,x) vec[i].push_back(x)
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-b+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
using namespace std;
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
ll T,n,m,MOD,p2,p5,pw[MAXN][2];int K;
ll q_pow(ll a,ll t,ll p,ll res=1)
{
    for(a%=p;t;t>>=1,(a*=a)%=p)
        if(t&1) (res*=a)%=p;return res;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b){x=1,y=0;return a;}
    ll d=exgcd(b,a%b,y,x);y-=(a/b)*x;return d;
}
ll Pw(ll n,ll p,ll pk)
{
    if(!n) return 1;ll res=1;
    res=q_pow(pw[pk][p==5],n/pk,pk);
    (res*=pw[n%pk][p==5])%=MOD;
    return (res*Pw(n/p,p,pk))%pk;
}
ll inv(ll n,ll p) {ll x,y;exgcd(n,p,x,y);return (x+p)%p;}
ll C(ll n,ll m,ll p,ll pk,int f)
{
    ll sum=0;for(ll i=n;i;i/=p) sum+=i/p;for(ll i=m;i;i/=p) sum-=i/p;
    for(ll i=n-m;i;i/=p) sum-=i/p;
    if(p==2&&f) sum--;if(sum>K) return 0;
    ll pn=Pw(n,p,pk),pm=Pw(m,p,pk),pz=Pw(n-m,p,pk);
    ll tmp=1;if(p==5&&f) tmp=inv(2,pk);
    pm=inv(pm,pk),pz=inv(pz,pk);
    return ((((q_pow(p,sum,pk)*pn)%MOD*pm)%MOD*pz)%MOD*tmp)%MOD;
}
ll exlucas(ll n,ll m,ll p,int f)
{
    return ((C(n,m,2,p2,f)*inv(p5,p2)%MOD*p5)%MOD+(C(n,m,5,p5,f)*inv(p2,p5)%MOD*p2)%MOD)%MOD;
}
void Print(ll a,int k)
{
    if(k==1) printf("%01lld
",a);
    if(k==2) printf("%02lld
",a);
    if(k==3) printf("%03lld
",a);
    if(k==4) printf("%04lld
",a);
    if(k==5) printf("%05lld
",a);
    if(k==6) printf("%06lld
",a);
    if(k==7) printf("%07lld
",a);
    if(k==8) printf("%08lld
",a);
    if(k==9) printf("%09lld
",a);
}
void work(ll n,ll m,int k,ll ans=0)
{
    p2=q_pow(2,k,inf),p5=q_pow(5,k,inf),MOD=p2*p5;
    if(n==m) ans=(q_pow(2,(n<<1)-1,MOD)-exlucas(n<<1,n,MOD,1)+MOD)%MOD;
    else 
    {
        ans=q_pow(2,n+m-1,MOD);
        lrep(i,((n+m)>>1)+1,n-1) (ans+=exlucas(n+m,i,MOD,0))%=MOD;
        if(!((n+m)&1)) (ans+=exlucas(n+m,(n+m)>>1,MOD,1))%=MOD;
    }
    Print(ans,k);
}
int main()
{
    pw[0][0]=pw[0][1]=1;
    rep(i,1,512) if(i%2) pw[i][0]=(pw[i-1][0]*i)%512;else pw[i][0]=pw[i-1][0];
    rep(i,1,1953125) if(i%5) pw[i][1]=(pw[i-1][1]*i)%1953125;else pw[i][1]=pw[i-1][1];
    while(~scanf("%lld%lld%d",&n,&m,&K)) {work(n,m,K);}
}