第一次224真是辣鸡
改完顺利AK
T1:
括号匹配很裸,用一个栈完事

1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4 #include<algorithm>
5 #include<cstdlib>
6 #include<cmath>
7 #include<vector>
8 #include<queue>
9 #include<map>
10 #define ll long long
11 #define inf 2147483611
12 #define MAXN 1001001
13 using namespace std;
14 inline int read()
15 {
16 int x=0,f=1;
17 char ch;ch=getchar();
18 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
19 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
20 return x*f;
21 }
22 char ch[MAXN],st[MAXN];
23 int tp,len;
24 int main()
25 {
26 freopen("a.in","r",stdin);
27 freopen("a.out","w",stdout);
28 scanf("%s",ch+1);
29 len=strlen(ch+1);
30 for(int i=1;i<=len;i++)
31 {
32 if(ch[i]=='('||ch[i]=='['||ch[i]=='{') {st[++tp]=ch[i];continue;}
33 if(!tp&&(ch[i]=='}'||ch[i]==']'||ch[i]==')')) {printf("Wrong");return 0;}
34 if(st[tp]=='('&&ch[i]==')') {tp--;continue;}
35 if(st[tp]=='['&&ch[i]==']') {tp--;continue;}
36 if(st[tp]=='{'&&ch[i]=='}') {tp--;continue;}
37 printf("Wrong");return 0;
38 }
39 if(!tp) printf("OK");
40 else printf("Wrong");
41 }
T2:
一个矩形,要通过一个L型的通道:
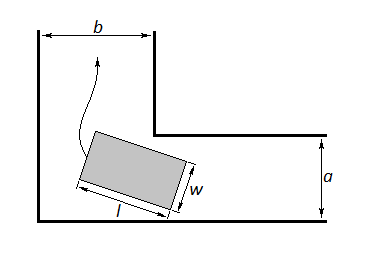
已知l,求wmax(w<=l)矩形的可以随意滑动
思路:
首先可以把L型外侧看作为坐标轴,而L即为一条直线,因为已知截距不会求一般式,所以我放弃了三分,用了馒头的想法,然后24分
mmp
然后我写了正解:三分
首先我们要求出这个直线的一般式,然后求出L型内侧拐点到直线的距离(这个还是会的)
这样的话所求w即为该距离的最小值,但是当存在一个直线的位置使拐点在直线下方,则无解
所以我们三分的范围为0-l,然后正常的三分就好了

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdlib> 6 #include<cmath> 7 #include<vector> 8 #include<queue> 9 #include<map> 10 #define ll long long 11 #define inf 2147483611 12 #define MAXN 100101 13 using namespace std; 14 inline int read() 15 { 16 int x=0,f=1; 17 char ch;ch=getchar(); 18 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 19 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 20 return x*f; 21 } 22 int a,b,L; 23 double ans(double A) 24 { 25 double B=sqrt((L*L-A*A)),C=-A*B; 26 if(a*A+b*B+C<0) return -1.0; 27 return (a*A+B*b+C)/L; 28 } 29 int main() 30 { 31 freopen("b.in","r",stdin); 32 freopen("b.out","w",stdout); 33 a=read(),b=read(),L=read(); 34 if(a>b) swap(a,b); 35 if(L<=a) {printf("%d.0000000",L);return 0;} 36 if(L>a&&L<=b) {printf("%d.0000000",a);return 0;} 37 double l=0.0,r=(double)L; 38 for(int i=1;i<=150;i++) 39 { 40 double m1=(r-l)/3.0+l,m2=r-(r-l)/3.0; 41 if(ans(m1)<0.0||ans(m2)<0.0) {printf("My poor head =(");return 0;} 42 if(ans(m1)<ans(m2)) r=m2; 43 else l=m1; 44 } 45 printf("%.7lf",ans(r)); 46 }
T3:
一个树,删除一条边花费为1,加入一条边花费为1,求最小花费使该树变为一个环
思路:
首先我们可以知道对于每个入度为一的点,这条边是不用被删除的
然后我们随便找一个叶子节点,dfs
dfs时记一下上一次从哪里来,这样就会避免重复查找
然后对于每一个入度>2的点我们最多保留两条边,其他边都一定要被删除,然后直接dfs就好了

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdlib> 6 #include<cmath> 7 #include<vector> 8 #include<queue> 9 #include<map> 10 #define ll long long 11 #define inf 2147483611 12 #define MAXN 100101 13 using namespace std; 14 inline int read() 15 { 16 int x=0,f=1; 17 char ch;ch=getchar(); 18 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 19 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 20 return x*f; 21 } 22 int n,ind[MAXN]; 23 int ans,to[MAXN],first[MAXN],next[MAXN],cnt; 24 void add(int u,int v) {next[++cnt]=first[u],first[u]=cnt,to[cnt]=v,ind[v]++;} 25 void dfs(int x,int lt) 26 { 27 for(int i=first[x];i;i=next[i]) 28 { 29 if(to[i]==lt) continue; 30 dfs(to[i],x); 31 if(ind[to[i]]>2) {ind[x]--;ans+=(ind[to[i]]-2)*2;} 32 } 33 } 34 int main() 35 { 36 freopen("c.in","r",stdin); 37 freopen("c.out","w",stdout); 38 n=read(); 39 int a,b; 40 for(int i=1;i<n;i++) {a=read(),b=read();add(a,b);add(b,a);} 41 for(int i=1;i<=n;i++) if(ind[i]==1) {dfs(i,0);break;} 42 printf("%d",ans+1); 43 }
