迭代法

hdu 3809;

一，迭代法 的基本概念：

迭代法事一种常用算法设计方法。迭代式一个不断用新值取代变量的旧值，或由旧值递推出变量的新值的过程。迭代机制需要以下一些要素：

①迭代表达式；

②迭代变量；

③迭代初值；

④迭代终止条件。

当一个问题的求解过程能够由一个初值使用一个迭代表达式进行反复的迭代时，便可以用效率极高的重复程序描述，所以迭代也是用循环结构实现，只不过要重复的操作是不断从一个变量的旧值出发计算它的新值。其基本格式如下：

迭代变量赋初值；

循环语句

{

计算迭代式；

新值取代旧值；

}

”迭代 “一词在wiki百科 中的定义如下：

迭代 是数值分析中通过从一个初始 估计 出发寻找一系列近似解 来解决问题（一般是解方程或者方程组）的过程，为实现这一过程所使用的方法统称为迭代法 （Iterative Method）。

跟迭代法相对应的是直接法 （或者称为一次解法 ），即一次性解决问题，例如通过开方解决方程x² = 4 。一般如果可能，直接解法总是优先考虑的。但当遇到复杂问题时，特别是在未知量很多，方程为非线性时，我们无法找到直接解法（例如五次以及更高次的代数方程没有解析解阿贝耳定理 ），这时候或许可以通过迭代法寻求方程（组）的近似解。 ，参见

最常见的迭代法是牛顿法。其他还包括最速下降法 、共轭迭代法、变尺度迭代法 、最小二乘法、线性规划、非线性规划 、单纯型法 、惩罚函数法 、斜率投影法 、遗传算法、模拟退火等等。

其中这里要指出一下的是 牛顿迭代法 ，是一种较为常用的迭代法。

牛顿法 （Newton's method ）又称为牛顿-拉夫逊方法（Newton-Raphson method ），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x ) 的泰勒级数的前面几项来寻找方程f (x ) = 0 的根。

首先，选择一个接近函数f (x ) 零点的x₀ ，计算相应的f (x ₀ ) 和切线斜率f '(x₀ ) （这里f ' 表示函数f的导数）。然后我们计算穿过点(x ₀ ,f (x₀ )) 并且斜率为f '(x ₀ ) 的直线和x轴的交点的x 坐标，也就是求如下方程的解：

我们将新求得的点的x 坐标命名为x₁ ，通常x ₁ 会比x₀ 更接近方程f (x ) = 0 的解。因此我们现在可以利用x₁ 开始下一轮迭代。迭代公式可化简为如下所示：

已经证明，如果f ' 是连续 的，并且待求的零点x是孤立的，那么在零点x 周围存在一个区域，只要初始值x₀ 位于这个邻近区域内，那么牛顿法必定收敛。 并且，如果f '(x ) 不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。

第一个例子

求方程f (x ) = cos(x ) − x ³ 的根。两边求导，得f  '(x ) = −sin(x ) − 3x² 。由于cos(x ) ≤ 1（对于所有x ），以及x ³ > 1（对于x >1），可知方程的根位于0和1之间。我们从x₀ = 0.5开始。

第二个例子

牛顿法亦可发挥与泰勒展开式，对于函式展开的功能。

求a的m次方根。

x ^m - a= 0

设f (x ) = x ^m − a ，f '(x ) = m x^{m − 1}

而a的m次方根，亦是x的解，

以牛顿法来迭代：

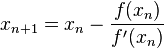
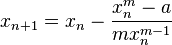
(或 )

另外，牛顿迭代法 在百度词条 中的定义：点击这里

二， 简单实例

例题一：

求Fibonacci数列。

1，1，2，3，5，8，13，21，34..... 此为Fibonacci数列。

输入：整数n(n>=3)

输出：n个Fibonacci数列

算法设计：基本迭代法

即

f(1)=f(2)=1;

f(n)=f(n-1)+f(n-2);    (n>=3)

C++实现如下：

#include<iostream>
using namespace std;
void f(int n)
{
	int f,f1,f2;
	f1=f2=1;
	cout<<f1<<" "<<f2<<" ";
	for(int i=3;i<=n;i++)
	{
		f=f1+f2;
		cout<<f<<" ";
		f1=f2;
		f2=f;
	}
	cout<<endl;
}
int main()
{
	int n;
	cin>>n;
	f(n);
	return 0;
}

10
1 1 2 3 5 8 13 21 34 55
Press any key to continue

例题二：

编写一个程序，求以下方程的根：

x³-5x²+6x-80=0

算法设计：牛顿迭代法

利用牛顿迭代公式 x(n+1)=x(n)-f(x(n))/f'(x(n));

循环体为：

for(int i=0;i<n;i++)
{
        x1=x0-f(x0)/df(x0);
        x0=x1;
}

其中n为迭代次数，该值越大根值越精确；x0为在方程根取值范围内的任意值，作为初始迭代的条件。

C++实现如下：

#include<iostream>
using namespace std;
float f(float x)
{
	float y;
	y=x*x*x-5.0*x*x+16.0*x-80.0;
	return y;
}
float df(float x)
{
	float y;
	y=3.0*x*x-10.0*x+6;
	return y;
}
int main()
{
	float x0,x1;
	int n;
	cout<<"输入x0:";
	cin>>x0;
	cout<<"迭代次数:";
	cin>>n;
	for(int i=0;i<n;i++)
	{
		x1=x0-f(x0)/df(x0);
		x0=x1;
	}
	cout<<"方程的根:x="<<x0<<endl;
	return 0;
}

输入x0:2
迭代次数:10
方程的根:x=5.15874
Press any key to continue

输入x0:2
迭代次数:100
方程的根:x=5
Press any key to continue