<前言>
有这么一个神奇的ppt:3.郭华阳《RMQ与LCA问题》
讲了LCA和RMQ的玄妙关系。两者如何在优秀的时间内相互转化。
也讲述了克鲁斯卡尔重构树内容。
本篇blog就是相关学习总结。
<正文>
RMQ&LCA学习笔记
引入
关于LCA最近公共祖先和RMQ区间最值问题。
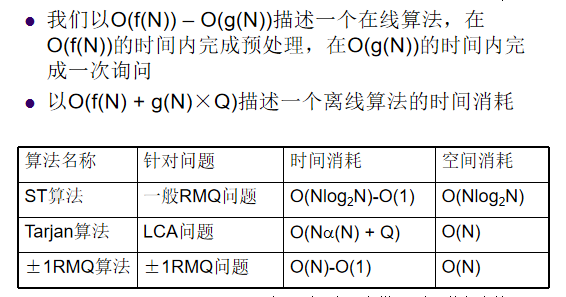
我们首先看一下复杂度。
当LCA问题与RMQ问题可以相互转换时,可以大大拓宽其应用面。
今天我任务的二分之一就是大概复述一遍这个内容,避免以后自己忘掉。
RMQ->LCA:笛卡尔树
还有lzh大佬的pdf讲案。
定义及应用
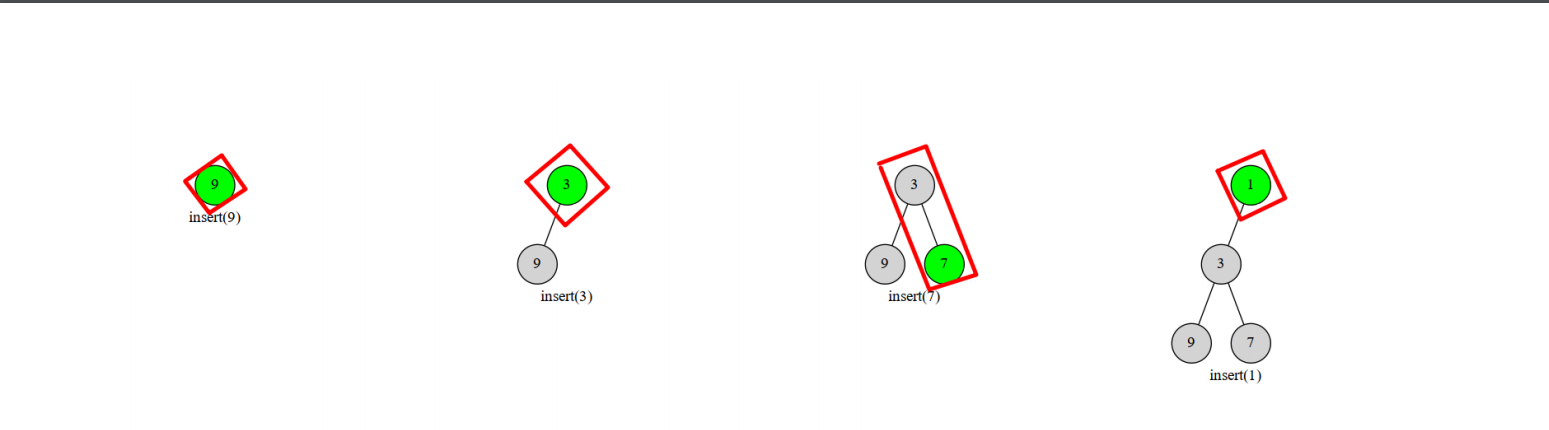
笛卡尔树是一种二叉树,每一个结点由一个键值二元组((k,w))构成。
要求(k)满足二叉搜索树的性质,而(w)满足堆的性质。
对于长度为n的序列(a_i) :
-
找到最小值(A_k)位置k,建立根节点(T_k),点权为(A_k)。
-
将(1...k-1)递归建树作为(T_k)的左子树。
将(k+1...n)递归建树作为(T_k)的右子树。
这样建完一棵树之后,显然这是一棵优先级树。大概长这个样子:
区间(mathrm{[l,r]})之间的最值显然就是树中(T_l)与(T_r)的LCA。
其实,笛卡尔树满足以下特征:
- 它的中序遍历是原数列。
- 任意一个节点的值都 < 它的两个儿子节点的值。
- 任意两点的(LCA)就是它们的(RMQ)。
支持的复杂度(以Tarjan离线LCA为例)大概就是 预处理(O(n))+每次查询(O(1))。
emmm感觉和RMQ没啥区别。但是这给更多的操作提供了条件,比如树上dp如何如何的。
还有应用:求左右延伸区间,(O(n))预处理+(O(1))询问。
构造
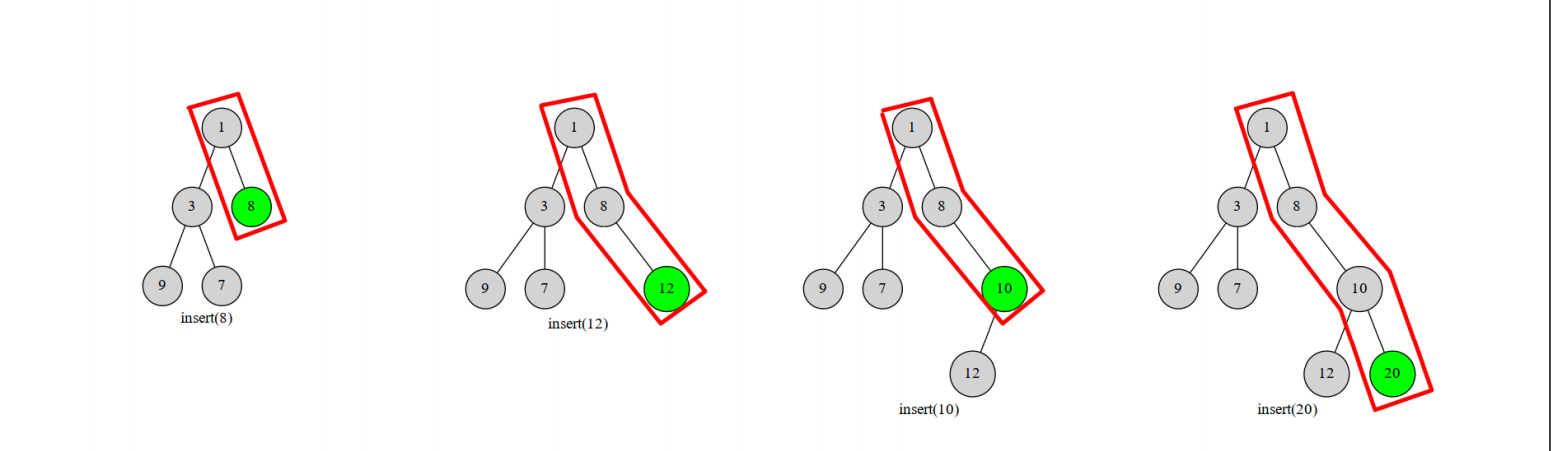
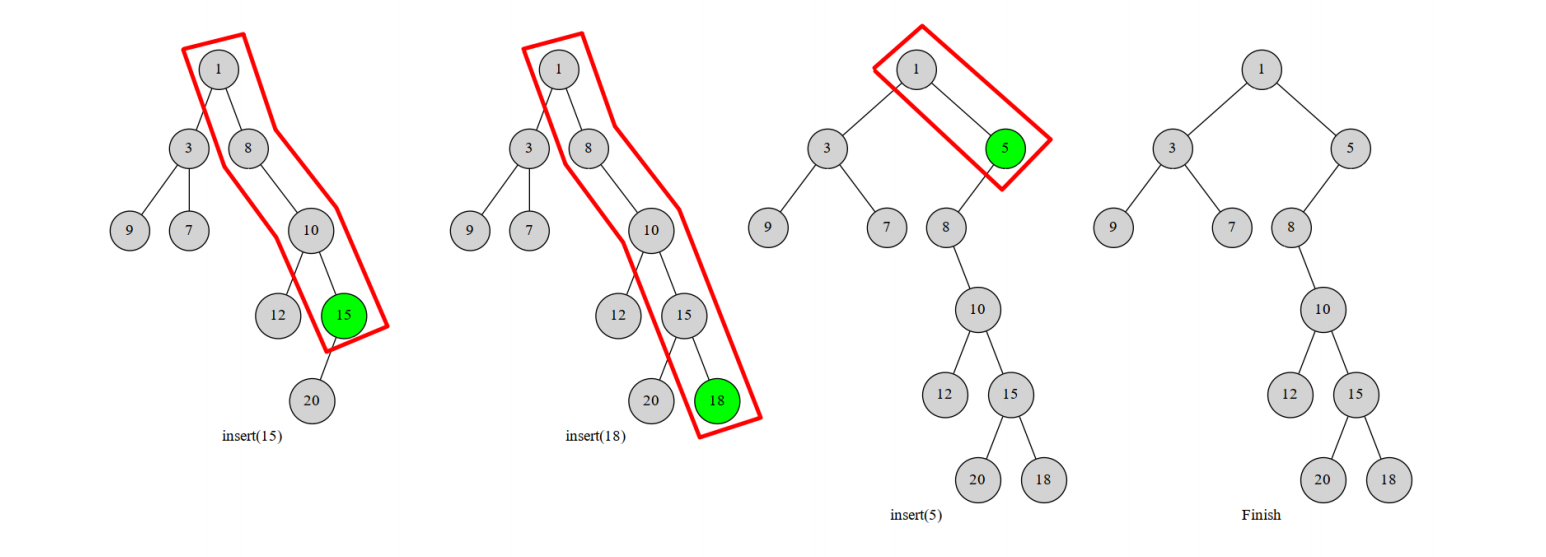
转换有多种方式,但最优秀的是(O(n))建树。
用到一个单调栈维护最右边的链,是一种妙啊巧妙的方法。
流程如下:
- 1.单调递增(or递减)的单调栈维护最右边的树链。
- 2.对于新增节点x,弹出的那些数直接挂在当前节点x左子树
- 3.其实更像是把整一棵树直接挂上去。
图解样例:
还是十分欢乐的。
建树(mathrm{Code:})
//stk[]为栈,存储key(下标),h[]数组存储值
for (int i = 1; i <= n; i++)
{
int k = top;
while (k > 0 && h[stk[k]] > h[i]) k--;
if (k) rs[stk[k]] = i; // rs代表笛卡尔树每个节点的右儿子
if (k < top) ls[i] = stk[k + 1]; // ls代表笛卡尔树每个节点的左儿子
stk[++k] = i;
top = k;
}
应用
主要是最值延展。
还有

这个最大矩阵问题。
具体题解不说了可以参考上面的blog。
毕竟本篇重点不在笛卡尔树。
LCA->RMQ:欧拉序O(n)LCA
比起笛卡尔树,这个我觉得是更大的扩展,毕竟复杂度变优秀了。
预处理(O(n(dfs)+n log n(ST表))),询问(O(1)(ST表)),还是在线算法。
可能预处理复杂度大一点,但比起离线Tarjan在线还是有优势的。
推荐LCA博文 还是很不错的。
定义及要点
对有根树T进行DFS,将遍历到的结点按照顺序记下,我们将得到一个长度为(2N – 1)的序列,称之为T的欧拉序列F。
每个结点都在欧拉序列中出现,我们记录结点u在欧拉序列中第一次出现的位置为pos(u)。


操作十分简单明了。
根据DFS的性质,对于两结点u、v,从(pos(u))遍历到(pos(v))的过程中经过LCA(u, v)有且仅有一次,且深度是深度序列(B[pos(u)…pos(v)])中最小的。
也就是说我们的LCA就是(pos(u))到(pos(v))中深度最小的那个点。
构造与解决
然后就十分快乐了。
开局一次dfs,反手一个ST表,每个询问(O(1))解决。
都是学过的知识点的总结,也没啥流程。
ST表离线操作不会的话我也无能为力。
至此,LCA与RMQ问题可以互相在(O(n))时间内转换。
(mathrm{Code:})
struct LCA
{
int dfn[N << 1], tr[N], d[N << 1];
int vs;
void dfs(int u, int fa, int deh)
{
dfn[++vs] = u;//dfs序
d[vs] = deh; //每个点深度
tr[u] = vs; //第一次出现位置,即pos[]
for(int i = T.fl[u]; i; i = T.net[i])
{
int v = T.to[i];
if(v == fa)continue;
dfs(v, u, deh + 1);
dfn[++vs] = u; //每次出子节点再加入一次
d[vs] = deh;
}
}
int f[N << 1][31];
inline int calc(int x, int y)
{
return d[x] < d[y] ? x : y;
}
int lca(int x, int y)
{
int l = tr[x], r = tr[y];
if(l > r)swap(l, r);
int block = log(r - l + 1) / log(2);
return dfn[calc(f[l][block], f[r - (1 << block) + 1][block])];
//快乐的LCA
}
void pre()
{
for(int i = 1; i <= vs; ++i)
f[i][0] = i;
for(int i = 1; i < 30; ++i)
for(int j = 1; j + (1 << i) - 1 <= vs; ++j)
f[j][i] = calc(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
//ST表预处理
}
void work(int root, int m)
{
dfs(root, 0, 1);
pre();
for(int i = 1; i <= m; ++i)
{
int l = read(), r = read();
printf("%d
", lca(l, r));
}
}
};
应用
要说(O(n))LCA的应用,那就多了。
对于修改操作,你甚至可以每次都重新构造,完全莫得问题。
总结
RMQ&LCA算法关系图

然后就是可以各种转换各种乱搞。
高手训练上有相关练习题。
Kruskal重构树&顺序生成森林
引出
以一道例题引出。
题目大意:
有修改操作(删边)的最小瓶颈路问题,多组询问。
结点数 N ≤ 1000; 边数 M ≤ 100000;
操作数 Q ≤ 100000; 删边操作 D ≤ 5000;
类Prim算法复杂度(O(N^2)),可过,但不够优秀。
复杂度瓶颈:边数过多;询问的复杂度过高。
然后我们需要找到方法解决这个问题。
最小生成森林
定义:其实就是从一棵树变成了一片树,没啥本质区别。
- 引理一:任意询问可以在G的最小生成森林中找到最优解。证明。
根据引理,我们只需要保存所有树边即可,这样边数下降到(O(N))级别,第一个问题被解决。
关于实现:其实就是不用判定连了多少条边,有多少连多少连到底就行。
(mathrm{Code:})
for(int i = 1; i <= len; ++i)
{
int u = F.get(e[i].x), v = F.get(e[i].y);
if(u != v)
{
F.f[u] = v;
sum += e[i].z;
T.inc(e[i].x, e[i].y, e[i].z);
T.inc(e[i].y, e[i].x, e[i].z);
}
}
没错你没看出任何区别。但是在一些不连通的图中会有差别。
Kruskal重构树
对于第二个问题,我们需要找到生成森林上两点间路径上的最大值。
你当然可以用LCT或者树剖来解决这个问题,搞不好倍增也行。
但是关于本专题有一个十分方便的算法:Kruskal重构树。
重构树是啥自行搜索即可,我们说说这有啥用。
我们进行Kruskal算法时,进行了排序,故关于当前边连接的两个集合,它们间路径最大值必定是当前边。
根据这个原理,我们对这颗生成树进行重构。结果如下:
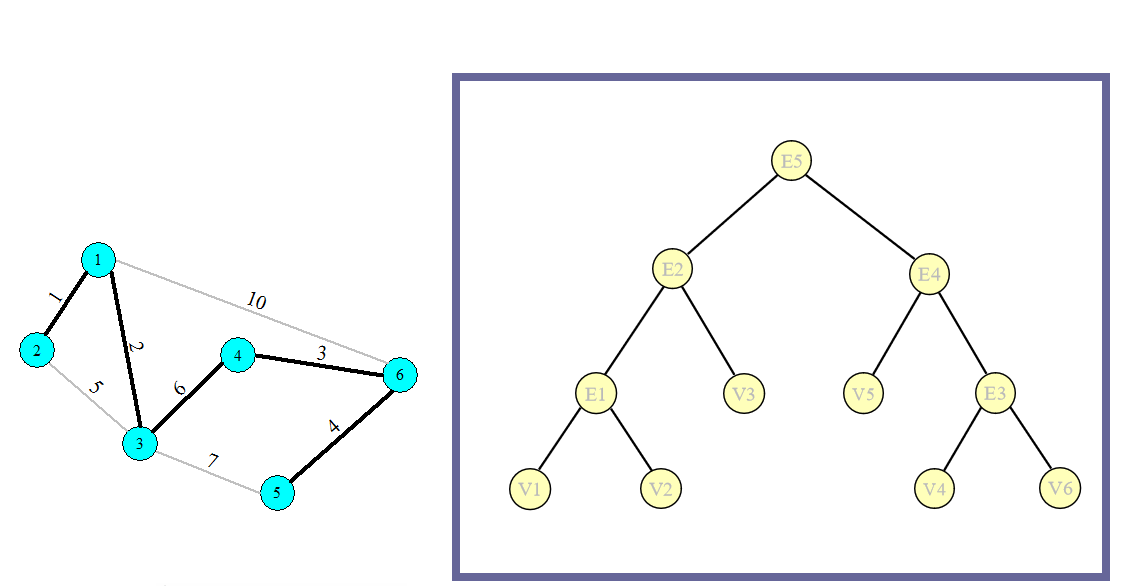
其中E代表边,V代表点。
我们可以发现,重构树中两点间路径上最长边就是两点LCA。
这就舒服了,接下来想怎么求LCA就怎么求。
用上个离线Tarjan或欧拉序LCA都不是问题。每次操作完更新一次,处理得可得劲了。
算法流程:
-
1.生成结束时的最小生成森林和顺序森林;
-
2.从后往前完成操作:对于删边操作,重新生成最小生成森林和顺序森林;
对于连续的询问操作,将其作为离线LCA询问在顺序森林上处理;
-
3.输出答案;
同时你可以据此更方便得解决更多问题。
就是代码实现有点问题了,挺繁琐的,但也不算难。
重构树(mathrm{Code:})
US_find F;
F.build(n + m);
int cnt = n;
sort(e + 1, e + m + 1, cmp);
for(int i = 1; i <= m; ++i)
{
int u = F.get(e[i].x), v = F.get(e[i].y);
if(u != v)
{
F.f[u] = F.f[v] = ++cnt;
a[cnt] = e[i].z;
T.inc(cnt, u);
T.inc(cnt, v);
}
}
for(int i = 1; i <= n; ++i)
if(!vis[i])
{
dfs(F.f[i], 0);
dfs1(F.f[i], F.f[i]); //树剖LCA
}
例题
【高手训练】【图论】汉堡店
首先最小生成树是必要的,我们尽量使除此边以外的边小,MST很稳。
答案(frac{A}{B}),我们需要使A尽量大,B尽量小。
但我们也不能一味找(P_i)最大的两家店或者找MST中最大的那条边。因为可能存在相对折中的方案使答案最大。
但是我们发现数据范围允许我们(n^2)枚举每一对汉堡店并验证其相连边(x,y)。
-
若加入边(x,y),若在生成树中,直接计算贡献即可。
-
若不在生成树中,则需删去一边,即生成树中x,y路径上的最大边。
这就转换成了最小瓶颈路问题,直接在原树上找就行了,复杂度(O(log n))
流程如下:
- 1.原图求MST,预处理最小瓶颈路,可以使用MST+倍增或重构树。
- 2.枚举每对边,若不在生成树中找路径上最大边删去并计算贡献。
So easy,isn't it?
(mathrm{Code(倍增)}:)
#include<bits/stdc++.h>
#define N 2010
using namespace std;
int n;
struct Tree
{
int to[N << 1], net[N << 1], len, fl[N];
double w[N << 1];
inline void inc(int x, int y, double z)
{
to[++len] = y;
w[len] = z;
net[len] = fl[x];
fl[x] = len;
}
} T;
struct hamber_store
{
int x, y;
double P;
} a[N] = {};
struct rode
{
int x, y;
double z;
} e[N * N] = {};
int len = 0;
struct US_find
{
int f[N], n;
inline void build(int m)
{
n = m;
for(int i = 1; i <= n; ++i)
f[i] = i;
}
int get(int x)
{
return x == f[x] ? x : f[x] = get(f[x]);
}
};
int read()
{
int s = 0, w = 1;
char c = getchar();
while((c < '0' || c > '9') && c != '-')
c = getchar();
if(c == '-')w = -1, c = getchar();
while(c <= '9' && c >= '0')
s = (s << 3) + (s << 1) + c - '0', c = getchar();
return s * w;
}
inline bool cmp(rode x, rode y)
{
return x.z < y.z;
}
int d[N] = {};
int f[N][35] = {};
double z[N][35] = {};
void dfs(int u, int fa)
{
for(int j = 1; j <= 30; ++j)
{
if(d[u] < (1 << j))break;
f[u][j] = f[f[u][j - 1]][j - 1];
z[u][j] = max(z[u][j - 1], z[f[u][j - 1]][j - 1]);
}
for(int i = T.fl[u]; i; i = T.net[i])
{
int v = T.to[i];
if(v == fa)continue;
d[v] = d[u] + 1;
f[v][0] = u;
z[v][0] = T.w[i];
dfs(v, u);
}
}
int lca(int x, int y)
{
if(d[x] < d[y])swap(x, y);
int t = d[x] - d[y];
for(int i = 0; i <= 30; ++i)
if((1 << i)&t)x = f[x][i];
for(int i = 30; i >= 0; --i)
if(f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
if(x == y)return x;
return f[x][0];
}
double ask(int x, int LCA)
{
double maxn = 0.0;
int tmp = d[x] - d[LCA];
for(int i = 0; i <= 30; ++i)
if(tmp & (1 << i))
{
maxn = max(maxn, z[x][i]);
x = f[x][i];
}
return maxn;
}
int main()
{
memset(z, -0x3f, sizeof(z));
n = read();
for(int i = 1; i <= n; ++i)
{
a[i].x = read();
a[i].y = read();
a[i].P = 1.0 * (double)read();
}
for(int i = 1; i <= n; ++i)
for(int j = i + 1; j <= n; ++j)
{
double t = sqrt((a[i].x - a[j].x) * (a[i].x - a[j].x) + (a[i].y - a[j].y) * (a[i].y - a[j].y));
e[++len] = (rode)
{
i, j, t
};
}
sort(e + 1, e + len + 1, cmp);
US_find F;
F.build(n);
double sum = 0.0;
for(int i = 1; i <= len; ++i)
{
int u = F.get(e[i].x), v = F.get(e[i].y);
if(u != v)
{
F.f[u] = v;
sum += e[i].z;
T.inc(e[i].x, e[i].y, e[i].z);
T.inc(e[i].y, e[i].x, e[i].z);
}
}
dfs(1, 0);
double maxx = 0.0;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
{
int LCA = lca(i, j);
double maxn = max(ask(i, LCA), ask(i, LCA));
maxx = max(maxx, (a[i].P + a[j].P) * 1.0 / (sum - maxn));
}
printf("%.2lf
", maxx);
return 0;
}
其实套路都这样差不多,以下几题很好:
总结
没啥好总结的。
大概就是多了一些奇怪的点子。
以后看到诸如区间最值延展、瓶颈路问题、奇怪复杂度LCA时能有更多的想法
<后记>
学习笔记,我不确定以后的自己看不看得懂,但是写写就挺好。
要开最短路了,回见,zqy!