【Educational Codeforces Round 87 (Rated for Div. 2)】前4题

zoukankan html css js c++ java

【Educational Codeforces Round 87 (Rated for Div. 2)】前4题
<前言>

时间(2020.05.18)，写出三题，罚时C1一次（大号）。小号无罚时。（过于真实

无rating。

只含前4题因为我只会前4题。

<考试过程>

A题上来先秒为敬。小号交一发没问题，稍微改改大号走起。

B稍微想了一下就发现了（真tm妙）规律，然后小号一发就A，大号走起。

目前为止十分顺利，小号都一遍A。

C1直接tm就没了。自己手推的公式全部错的，最后还得借助循环计算（白嫖(jh)代码）。然后觉得稳了，直接交大号。

[Wrong Answer On Test 3 ]
绝啦！

稍微改了一下，小号试水，tm直接A了，大号稍微改一下就A了。

然后C2，剩下时间都在想。不知不觉考试结束。

Solution

A. Alarm Clock

题目大意

一个人睡着后(b)分钟，第一个闹钟响了把他吵醒。我们假设只有闹钟能叫醒他。

他起床后，他可以继续睡或起床。若总睡眠时间不到(a)分钟，则他会定一个(c)分钟后响的闹钟，然后睡觉，睡着需要花费(d)分钟。

问多久之后能睡满(a)分钟起床。若不能到(a)分钟则输出(-1).

Answer

(sb)题，首先判断第一次醒来时到了a分钟没有，如果到了起床，没到继续睡。

如果继续睡，判断c是否大于d，若不是则输出(-1),否则计算每次能睡多久，剩下时间(b-a)除去这个次数向上取整就是定(c)分钟闹钟的个数。所以这个数乘(c)即可。

整一个特判题。

(mathrm{Code:})
```
#include<bits/stdc++.h>
#define int long long
using namespace std;
int a, b, c, d;
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
void write(int x)
{
    if(x > 9)write(x / 10);
    putchar(x % 10 + 48);
}
void work()
{
    int ans = 0;
    a = read();
    b = read();
    c = read();
    d = read();
    if(a <= b)
    {
        write(b);
        putchar(10);
        return ;
    }
    ans += b;
    if(d >= c)
    {
        puts("-1");
        return ;
    }
    int t = a - b;
    ans += ((t + c - d - 1) / (c - d) * c);
    write(ans);
    putchar(10);
}
main()
{
    int T = read();
    while(T--)
        work();
    return 0;
}
```
B. Ternary String

题目大意

每次给出一串只含1、2、3的数，问能够包括至少一个1、2、3的最短区间长度。

Answer

我们发现连续相同的数字有很多，进而想到这是(nleq200000)时必然的结果，因为若不多，则随便枚举。

然后就好办了，把一串相同的数压缩一下，记录每段连续个数。

然后我们三位三位去找1、2、3，可以证明如果有解一定会被我们找到。我们发现一组1、2、3的答案就是处在中间的数的个数+2，即左右各取一个数，中间全取。
```
For example：
111222233
压缩后1(3)2(4)3(2)
答案为2全取，1、3各取一个。
```
(mathrm{Code:})
```
#include<bits/stdc++.h>
#define int long long
#define N 200010
using namespace std;
int n, a[N] = {};
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
int cnt[N] = {};
void write(int x)
{
    if(x > 9)write(x / 10);
    putchar(x % 10 + 48);
}
void init()
{
    n = 0;
    memset(a, 0, sizeof(a));
    char c = getchar();
    while(c < '1' || c > '3')c = getchar();
    while(c <= '3' && c >= '1')
    {
        int t = c - '0';
        if(t == a[n])++cnt[n];
        else a[++n] = t, cnt[n] = 1;
        c = getchar();
    }
}
void work()
{
    int t[4] = {}, minn = INT_MAX;
    for(int i = 1; i <= n; ++i)
    {
        t[1] = t[2] = t[3] = 0;
        for(int j = i; j <= i + 2; ++j)
            t[a[j]] = 1;
        if(!t[1] || !t[2] || !t[3])continue;
        minn = min(minn, cnt[i + 1] + 2);
    }
    write(minn >= INT_MAX ? 0 : minn);
    putchar(10);
}
main()
{
    int T = read();
    while(T--)
    {
        init();
        work();
    }
    return 0;
}
```
C1. Simple Polygon Embedding

题目大意

这个问题的表述和C2的表述是一样的。唯一的区别是，在问题C1中，n总是偶数，在问题C2中，n总是奇数。

给出(n),要把点数为(2*n)的正多边形塞到一个正方形里，允许旋转。求这个正方形的最小边长。

Answer

这题就说来话长了。。。。

提供两种做法。

直接计算法

先上图

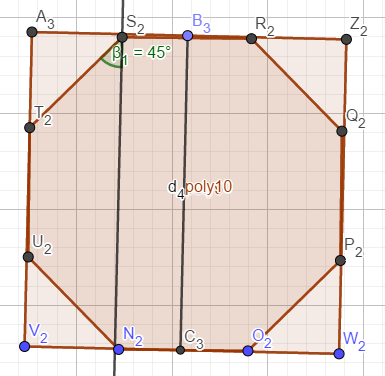
你发现我们计算得就是类似这种东西（次长对角线），每次往下偏转一个外角的角度，而每段的贡献是(cos(β)).

已知外角为(frac{2π}{2n}=frac{π}{n})，其中(π=acos(-1)),c++自带三角函数计算库。

那么容易发现答案为

[ans=2(frac{1}{2}+sum_{i=1}^{n/2}cos(i*frac{π}{n})) ]
(mathrm{Code:})
```
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
void write(int x)
{
    if(x > 9)write(x / 10);
    putchar(x % 10 + 48);
}
double ans = 0.0;
void work()
{
    n = read();
    ans = 0.0;
    double t = acos(-1) / n;
    for(int i = 1; i < n / 2; ++i)ans += cos(t * i);
    printf("%.10lf
", 1 + (ans * 2));
}
main()
{
    int T = read();
    while(T--)
        work();
    return 0;
}
```
数学公式法

我们试图用公式简洁地(O(1))计算答案。

观察下图：

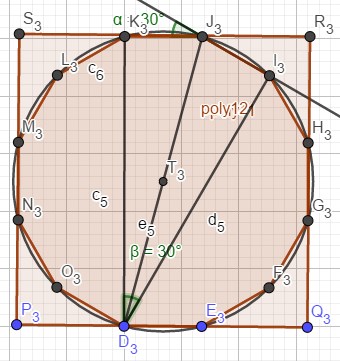
根据圆的有关知识，我们发现(β=α=frac{π}{n})，这个例子中外角为(30°)

答案为线段(K_3D_3)，我们已知(K_3J_3=1)，而(∠K_3D_3J_3=frac{1}{2}∠K_3D_3I_3=frac{π}{2n})然后就可以计算

[ans=frac{1}{tan(frac{α}{2})}=frac{1}{tan(frac{π}{2n})} ]
(mathrm{Code:})
```
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
double ans = 0.0, pi = acos(-1);
void work()
{
    n = read();
    printf("%.10lf
", 1 / tan(pi / 2 / n));
}
main()
{
    int T = read();
    while(T--)
        work();
    return 0;
}
```
这就完啦！

C2. Not So Simple Polygon Embedding

题目大意

见C1

Answer

这题，同样我们有两种写法，直接计算和公式计算。

但是我还得讲讲自己当时的思路。

在此之前得先说说什么情况最优

最优情况

对于任意奇数的n，逆时针倾斜45°是最优情况。如图

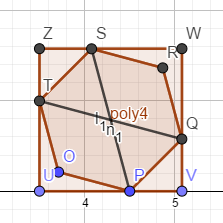
若继续旋转，会使(TQ)占用更长，所需正方形边长更长，故不优。

而往回转一点，就会使(SP)占用更长，所以现在这种情况就是最优。

直接计算

我们把每个(ans)拆成两部分分别直接计算。如上图中的(UV=UP+PV)

具体推导和C1差不多，就不讲了，挺暴力的。

(mathrm{Code:})
```
#include<bits/stdc++.h>
using namespace std;
int n;
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
double ans = 0.0, pi = acos(-1);
void work()
{
    n = read();
    ans = 0.0;
    double t = pi / 4;
    while(-(pi / 2 + 1e-7) <= t)t -= pi / n;
    t += pi / n;
    while(pi / 2 + 1e-7 >= t)ans += cos(t), t += pi / n;
    printf("%.10lf
", ans);
}
signed main()
{
    int T = read();
    while(T--)
        work();
    return 0;
}
```
数学推导1

我考场上没有写出来这题，但是当时考虑了很多，包括接下来推导的两个式子，但是出了一些问题。。。导致直接没掉。

下面是我考试的时候的推导，想要简单易懂的推导请下翻。

这题，我们直接~~霸王硬上弓~~画图解决

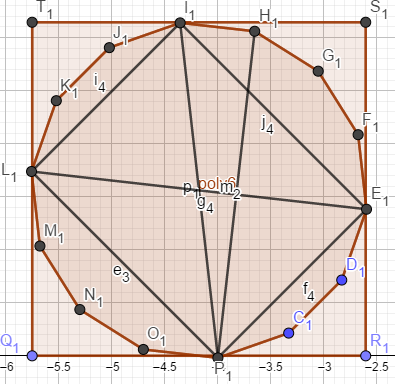
你看这幅图，我们设(Q_1P_1)为(x),(P_1R_1)为(y)，则(ans=x+y).此时我们再找找有什么等量关系。

我们发现(L_1P_1=sqrt{2}x,P_1E_1=sqrt{2}y),然后(L_1E_1)可求，设为(a)

可列出

[egin{aligned} &2(x^2+y^2)=a^2\ &=>x^2+y^2=frac{a^2}{2} end{aligned} ]
然后我们要求出(x+y),则需求出((x+y)^2=x^2+2xy+y^2).

即需再求出(xy)就可以算得答案

在矩形(L_1P_1E_1I_1)中，可知(2xy=frac{L_1E_1 imes H_1P_1}{2}) 其中C1中我们讨论过(H_1P_1)求法即(frac{1}{tan(frac{π}{2n})})，而(L_1P_1=frac{H_1P_1}{cos(frac{π}{4n})}=frac{1}{sin(frac{π}{2n})})，然后

[egin{aligned} &ans=sqrt{x^2+y^2+2xy}=sqrt{frac{1}{2sin^2(frac{π}{2n})}+frac{cos(frac{π}{2n})}{sin^2(frac{π}{2n})}}\ &=sqrt{frac{cos^2(frac{π}{4n})}{sin^2(frac{π}{2n})}}=frac{cos(frac{π}{4n})}{2sin(frac{π}{4n})cos(frac{π}{4n})}=frac{1}{2sin(frac{π}{4n})} end{aligned} ]

以上为复杂方法，我考试的时候推得。（虽然当时把sin和tan搞反了结果一直死）

够(sb)吧？

下面是简便推导。

数学方法2（simple）

直接画图

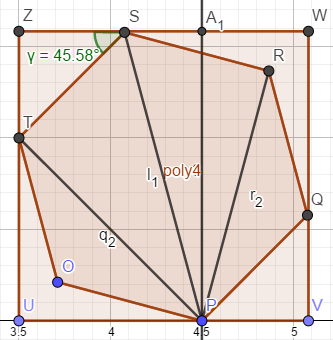
我们看到上图，决定从角出发，易得(∠RSW=π-frac{π}{4}-∠TSR=frac{3π}{4}-(π-frac{π}{n})=frac{π}{4n}),

再由(∠PSR=frac{π-frac{π}{n}}{2})，所以(∠PSA_1=frac{π}{2}-frac{π}{4n} =>∠SPA_1=frac{π}{4n})

然后直接tm绝啦，

[ans=PA_1=frac{cos(frac{π}{4n})}{sin(frac{π}{2n})}=frac{1}{2sin(frac{π}{4n})} ]
我觉得写得够易懂了。

差不多没了。

题外话：

当时推出等价的式子很多，什么(cos(frac{π}{4}) imes (1 + frac{1}{tan(frac{π}{2n})})),甚至没化简就瞎计算。

我也是服了自己。

(mathrm{Code:})
```
#include<bits/stdc++.h>
using namespace std;
int n;
int read()
{
    int s = 0, w = 1;
    char c = getchar();
    while((c < '0' || c > '9') && c != '-')
        c = getchar();
    if(c == '-')w = -1, c = getchar();
    while(c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
double pi = acos(-1);
void work()
{
    n = read();
    printf("%.10lf
", 0.5 / sin(0.25 * pi / n));
}
signed main()
{
    int T = read();
    while(T--)
        work();
    return 0;
}
```
<后记>

我觉得挺好

神(tmsb)结论题，真的是太(tm)有意思了。

听说D题(sb)数据结构，我看了一下，权值线段树，大概会了

。。。

妙啊。
查看全文

相关阅读:
用VS Code写C++程序如何运行
 DRF
DRF
DRF
DRF
DRF
DRF
DRF
DRF
DRF

原文地址：https://www.cnblogs.com/yywxdgy/p/12912525.html

【Educational Codeforces Round 87 (Rated for Div. 2)】前4题

<前言>

<考试过程>

Solution

A. Alarm Clock

题目大意

Answer

B. Ternary String

题目大意

Answer

C1. Simple Polygon Embedding

题目大意

Answer

直接计算法

数学公式法

C2. Not So Simple Polygon Embedding

题目大意

Answer

最优情况

直接计算

数学推导1

数学方法2（simple）

<后记>