权值线段树
顾名思义,就是以权值为下标建立的线段树。
现在让我们来考虑考虑上面那句话的产生的三个小问题:
1. 如果说权值作为下标了,那这颗线段树里存什么呢?
————— 这颗线段树中, 记录每个值出现的次数
2.权值很大怎么办?数组空间不够啊
————— 可以先离散化,再记录
3.那权值线段树到底是用来干嘛的呢?
————— 可以快速求出第k小值(其实主要还是为了主席树做铺垫啦)
那第k小值该怎么求呢???
从树根依次往下
若当前值K大于左儿子的值,则将K-=左儿子的值,然后访问右儿子
若当前值K小于左儿子的值,则直接访问左儿子
直到访问到叶子节点时,那么该节点所代表的那个数就是要求的第k小值
(因为其实节点中存的值是该值域区间的数字出现次数,所以第k小值前面一定会有k-1个数出现过)
代码就不给了
可持久化线段树
普通的线段树单点修改操作与区间查询自然不是问题
可是
假如当前询问若干修改操作之前的区间呢???
仔细想想
.
.
.
最暴力的做法无疑是对于每个修改操作重开一个线段树,
可是...这样显然空间开不下
那我们能不能优化一下呢
我们看看对于一次单点修改,这颗线段树操作前和操作后有什么不同吧
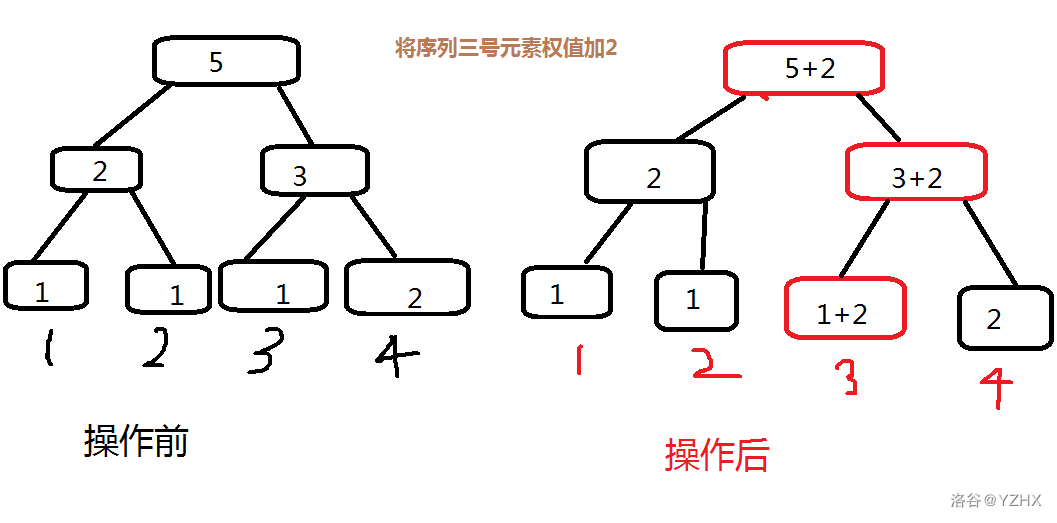
有点小丑,凑合着看
观察一下这两颗树,发现它们有区别的地方仅仅在于红色的方框
哎??? 这不是此次操作修改的目标元素到根的路径吗
既然只有这条路径变了,那我们就只复制这条路径好了,不用再复制整棵树了
所以空间就能大大的缩小了(log级)
代码 (洛谷模板)
#include<bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
#define get getchar()
#define in inline
in int read()
{
int x=1,t=0; char ch=get;
while((ch<'0' || ch>'9') && ch!='-') ch=get;
if(ch=='-') ch=get,x=-1;
while(ch<='9' && ch>='0') t=t*10+ch-'0', ch=get;
return t*x;
}
const int _=1e6+6;
int n,m,a[_],tot,root[_<<5],ls[_<<5],rs[_<<5],val[_<<5]; // ls == leftson,rs == rightson
in int build(int l,int r)
{
int now=++tot;
if(l==r)
{
ls[now]=rs[now]=0;
val[now]=a[l];
return now;
}
int mid=(l+r)>>1;
ls[now]=build(l,mid);
rs[now]=build(mid+1,r);
return now;
} //初始时的线段树
in int add(int k,int l,int r,int x,int t)
{
int now=++tot;
if(l==r)
{
val[now]=t;
ls[now]=rs[now]=0;
return now;
} //到了目标点,修改它
ls[now]=ls[k],rs[now]=rs[k];
int mid=(l+r)>>1;
if(x<=mid) ls[now]=add(ls[now],l,mid,x,t); //若目标点在原树的左子树上,则新建左儿子
else rs[now]=add(rs[now],mid+1,r,x,t); //若在右儿子上,同理
return now;
} //修改并添加新路径
in int query(int k,int l,int r,int x)
{
if(l==r) return val[k];
int mid=(l+r)>>1;
if(x<=mid) return query(ls[k],l,mid,x);
else return query(rs[k],mid+1,r,x);
} //查询
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;i++)
a[i]=read();
root[0]=build(1,n);
for(re int i=1;i<=m;i++)
{
int v=read(),o=read();
if(o==1)
{
int x=read(),y=read();
root[i]=add(root[v],1,n,x,y);
}
else
{
int x=read();
cout<<query(root[v],1,n,x)<<endl;
root[i]=root[v];
}
}
/*for(re int i=0;i<=10;i++)
{
cout<<"case #"<<i<<": ";
for(re int j=1;j<=n;j++)
cout<<query(root[i],1,n,j)<<' ';
cout<<endl;
}//打印每个历史版本 */
return 0;
}
/*
9.30 By yzhx
*/
静态主席树
可以用来求区间第k小/大值
说白了,就是把我们上面讲到的两个东西加起来,也就是用 可持久化权值线段树
再来看建树的具体步骤:
1.建一颗空线段树
2.依次把每个值加入这颗线段树(看做是一个修改操作)
查询:
(若当前查询的区间 l~r)
则直接把历史版本r 与 历史版本l-1, 直接加减,就能得到当前这个区间每个数出现的情况了
代码 (洛谷模板)
#include<bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
#define in inline
#define get getchar()
in int read()
{
int t=0,x=1; char ch=get;
while((ch<'0' || ch>'9') && ch!='-') ch=get;
if(ch=='-') ch=get,x=-1;
while( ch<='9' && ch>='0') t=t*10+ch-'0', ch=get;
return t*x;
}
const int _=2e5+5;
int tot,cnt,n,m,a[_],b[_],sum[_<<6],ls[_<<6],rs[_<<6],root[_];
in int build(int l,int r)
{
int now=++cnt;
if(l==r)
{
sum[now]=ls[now]=rs[now]=0;
return now;
}
int mid=(l+r)>>1;
ls[now]=build(l,mid),rs[now]=build(mid+1,r);
return now;
} //建一颗空树
in int add(int k,int l,int r,int x)
{
int now=++cnt;
if(l==r)
{
ls[now]=rs[now]=0;
sum[now]=sum[k]+1;
return now;
}
int mid=(l+r)>>1;
ls[now]=ls[k],rs[now]=rs[k],sum[now]=sum[k];
if(x<=mid) ls[now]=add(ls[k],l,mid,x);
else rs[now]=add(rs[k],mid+1,r,x);
sum[now]=sum[rs[now]]+sum[ls[now]];
return now;
} //加入每个元素
in int query(int k1,int k2,int l,int r,int x)
{
if(l==r) return a[l];
int mid=l+r>>1;
int t=sum[ls[k2]]-sum[ls[k1]];
if(x<=t) return query(ls[k1],ls[k2],l,mid,x);
else return query(rs[k1],rs[k2],mid+1,r,x-t);
} //查询
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;i++)
b[i]=a[i]=read();
sort(a+1,a+n+1);
tot=unique(a+1,a+n+1)-(a+1);
root[0]=build(1,n);
for(re int i=1;i<=n;i++)
{
// if(i<=tot) cout<<a[i]<<' ';
int x=lower_bound(a+1,a+tot+1,b[i])-a;
root[i]=add(root[i-1],1,tot,x);
}
//cout<<endl;
for(re int i=1;i<=m;i++)
{
int l=read(),r=read(),k=read();
printf("%d
",query(root[l-1],root[r],1,tot,k));
}
}