树状数组+(倍增/二分) & 冰火战士

前言: 2021省选最后三天了,开始补去年省选的题目...发现了毒瘤的冰火战士

题意

解释不清了...戳这里

Solution

对于每一时刻而言,冰火战士会分别组成上升和下降的序列,为了让冰火战士的能量总消耗尽量多
即: 冰人的前缀和与火人的后缀和尽可能相等
很容易想到,若冰人前缀和看做一条上升的直线,火人的后缀和视为下降直线,则最优决策点必定是两直线交点
也就是需要找到 冰人前缀和恰好小于火人后缀 or 火人后缀恰好小于冰人前缀

不难想到,这个可以用: 线段树二分 or 二分套树状数组
但是 对于 2e6 的数据而言显(bu)然(yiding)是跑不过的,这个时候就可以引出

树状数组倍增

按照下面的思路稍加拓展即可

树状数组倍增

假设当前要求的是 全局第k大:
那么我们建一棵权值树状数组
问题转化为了: 我们需要找到一个前缀和为k的位置

考虑树状数组的形态:

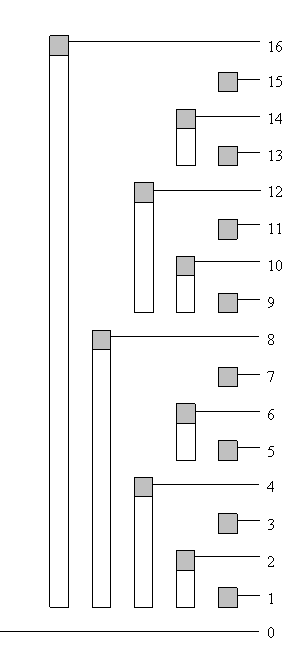
第i个节点会覆盖的区间长度恰好是 lowbit(i) 个位置的和,

考虑从 高位向低位 枚举
若加上接下来的 (2^x) 个元素后仍小于k
则加上此时下对应的树状数组节点
最后一步+1即可 (类似lca)
由于是高位向低位枚举,可保证每次新增的区间长度必定对应的是当前状态下的lowbit

code

int kth(int k)
{
    int now=0,s=0;
    for(re int i=21;i>=0;i--)
    {
        int to=now|(1<<i);
        if(to>n) continue; //若增加后的位置大于n,显然不对
        int x=s+sum[to];
        if(x<k) now=to, s=x;
    }
    return now+1; //找的是<=k的位置
}

code for Icefire

#include<bits/stdc++.h>
using namespace std;
#define re register
#define in inline
#define get getchar()
#define ll long long
in int read()
{
    int t=0,x=-1; char ch=get;
    while(ch<'0' || ch>'9') { ch=='-' ? x=-1: 1; ch=get;}
    while(ch<='9' && ch>='0') t=t*10+ch-'0', ch=get;
    return t;
}
const int _=2e6+23;
int Q,ic,fi,b[_],cnt,rf[_];
struct opt{
    int typ,t,x,y;
}a[_];
int sum1[_],sum0[_],S;
#define lowbit(x) (x&-x)
int query(int *sum,int x)
{
    int sss=0;
    while(x){ sss+=sum[x],x-=lowbit(x); }
    return sss;
}
void add(int *sum,int x,int k)
{    while(x<=cnt) sum[x]+=k,x+=lowbit(x); }

in void solve() //树状数组上倍增找到可能的两处交点
{
    int x=0,s1=0,s2=S; //s1是冰人前缀和,s2是火人后缀和
    for(re int i=21;i>=0;i--) //找到s1恰好小于s2的地方
    {
        int to=x|(1<<i);
        if(to>cnt) continue;
        int si=s1+sum0[to],sf=s2-sum1[to];
        if(si<sf) s1=si, s2=sf, x=to; 
    }
    int ansi=s1,ansf=min( query(sum0,x+1) , S-query(sum1,x+1) ),c1=x;
    // ansi存的是左边交点的值, ansf存的是右边
    x=0,s1=0,s2=S;
    for(re int i=21;i>=0;i--)
    {
        int to=x|(1<<i);
        if(to>cnt) continue;
        int si=s1+sum0[to],sf=s2-sum1[to];
        if(si<sf || sf==ansf) s1=si, s2=sf, x=to;
    }
    int c2=x;
    //c1,c2分别为对应的温度
    int mx=max(ansi,ansf);
    if(mx==0) puts("Peace");
    else if(ansi>ansf) printf("%d %d
",b[c1],ansi<<1); //b数组存的是离散化前对应的值
    else printf("%d %d
",b[c2],ansf<<1);
}

int main()
{
    Q=read();
    for(re int i=1;i<=Q;++i)
    {
        a[i].typ=read(), a[i].t=read();
        if(a[i].typ==1) b[++cnt]=a[i].x=read(), a[i].y=read();
    }
    sort(b+1,b+cnt+1);
    cnt=unique(b+1,b+cnt+1)-b-1;
    for(re int i=1;i<=Q;++i)
        if(a[i].typ==1) a[i].x=lower_bound(b+1,b+cnt+1,a[i].x)-b; //离散化
    for(re int i=1;i<=Q;++i)
    {
        if(a[i].typ==1)
        {
            if(a[i].t==0) { ic++; add(sum0,a[i].x,a[i].y); }
            else {fi++; add(sum1,a[i].x+1,a[i].y); S+=a[i].y;}
        }
        else
        {
            int id=a[i].t;
            if(a[id].t==0) { ic--; add(sum0,a[id].x,-a[id].y); }
            else { fi--; add(sum1,a[id].x+1,-a[id].y); S-=a[id].y;}
        }
        solve();
    }
    return 0;
}