约定:以下内容中\(*\)表示普通乘法,\(\cdot\)为点乘,\(\times\)为叉乘
代码中的*表示叉积,&表示点积, ^表示数乘
(当然是从xzy学长那儿学来的习惯啦)
文末有惊喜
前置知识
向量
向量基本概念与运算详见《2020人教版高中数学·选修一》
点积
又叫内积、数量积, 计算出来的结果是数值
几何意义: 第一个向量在第二个向量上的投影再乘上第二个向量的模长
其运算法则为:(\(\theta\)表示\(a\),\(b\)的夹角,\(0^\circ\le\theta\le180^\circ\))
若 \(\vec{a}(x_1,y_1),\vec{b}(x_2,y_2)\) 则
根据三角函数关系,易知:
- \(\theta=0^\circ\),那么它们的点积为他们的模长之积。
- \(\theta<90^\circ\),那么它们的点积为正
- \(\theta=90^\circ\),那么它们的点积为0。
- \(\theta>90^\circ\),那么它们的点积为负
叉积
又称外积、向量积,计算出来的结果是向量(垂直于两向量所在平面)
运算法则为:
若 \(\vec{a}(x_1,y_1),\vec{b}(x_2,y_2)\) 则
几何意义是两向量围成的有向面积, 因此叉积计算是没有交换律的
其方向可以通过右手法则来判定: 让\(\vec{a}\)穿过手心,然后四指卷曲从\(\vec{a}\)弯向\(\vec{b}\),大拇指伸直所指的方向就是叉积方向
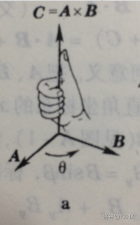
那么有:
- \(\vec{a}\times\vec{b}=0\) 则 \(\vec{a}\) 与 \(\vec{b}\) 平行
- \(\vec{a}\times\vec{b}>0\) 则 \(\vec{b}\) 在 \(\vec{a}\) 的逆时针方向
- \(\vec{a}\times\vec{b}<0\) 则 \(\vec{b}\) 在 \(\vec{a}\) 的顺时针方向
(大拇指朝纸里为负,朝纸外为正)
极坐标系
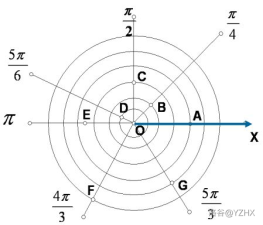
如上图
选取平面上一定点\(O\) 作为极点, 从极点引出一条射线(上图中的x轴) 作为极轴。
那么对于一个点\(B\),以极轴逆时针方向旋转到\(B\)的角度称为极角记为 \(\theta\), \(B\)到\(O\)的距离称为极径记为 \(\rho\)
那么此时平面上的任何一个点都可以通过((极径)\(\rho\),(极角)\(\theta\))的方式表示
极坐标系和平面直角坐标系(笛卡尔坐标系)的转化
若点\(A(x,y)\)的极坐标为\((\rho,\theta)\), 那么有:
又可推出:
那么极角 \(\theta=\arctan \frac{y}{x}\),在代码中可直接用 atan2(y, x)
点、线、角的相关运算
点与线
点P到直线 l 的距离
在直线\(l\)上任取两点A,B, P到\(l\)的距离D为:
点P到线段 AB 的距离
若点P向\(l_{AB}\)引一条垂线,垂足不在线段\(AB\)上,则距离为 \(min(|PA|,|PB|)\)
线与线
判断线段是否相交
可以用快速排斥实验和跨立实验
其中快速排斥实验大意是:若两个以给定带测验的线段为对角线的矩形,矩形边框不相交,则两线段一定不相交。否则,不一定相交。
主要来讲讲跨立实验:
思路:两条线段相交,则对于两条线段各自满足,另一条线段的两端一定分别位于该点两侧(也就是“跨立”)
对于跨立的判定:

上图中,观察到,一条线段CD若满足跨立,则\(\vec{CA}\times\vec{CD}\)的方向应与\(\vec{CD}\times\vec{CB}\)方向相同(注意先后顺序)
对应表达式为:
但是不难发现上图中仅有CD满足跨立,而AB不满足,即:
(搞不清楚的话,可以通过右手定则找一找方向)
求两线段交点
若存在线段交点,则线段交点即为直线交点,那么只需判断是否有交,再找到直线交点就好了
直线交点
(从xzy学长的博客里嫖来的图)
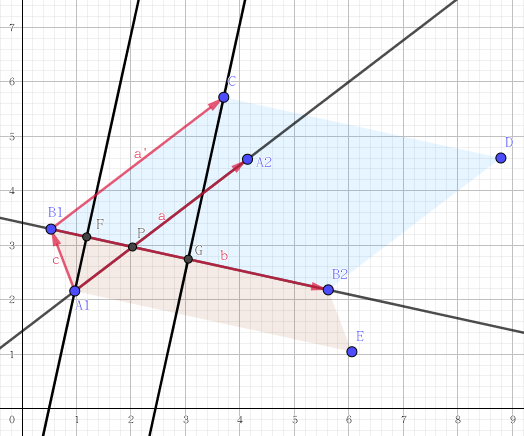
不妨设点\(P\),可通过 \(A1+\lambda\vec{a}\) 得到
根据相似三角形(面积比—>线段比),则
即:
角
向量旋转

(上图中 \(l^2=x^2+y^2\))
根据三角关系得:
(不记得了,也可通过图中式子经三角恒等变换推出)
极角排序
-
法1:(时间更快)
根据前文提到的 atan2(y,x) 这个函数的返回值(极角)作为键值,利用sort排序 -
法2:(精度更高)
利用叉积的正负性作为键值,利用sort排序
多边形相关
叉积求面积
计算方法:
按顺序将相邻顶点与原点构成的向量的叉积除以2依次累加, 所得之和就是该封闭多边形的面积
具体过程如下图:
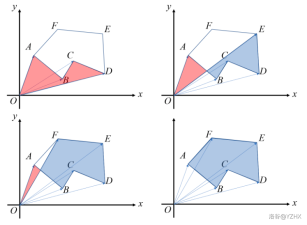
因为叉积是两向量所夹的平行四边形的有向面积,而对于一个封闭图形顶点A,一定会存在两个顶点B、C使得\(\vec{OA}\times\vec{OC}\)、\(\vec{OB}\times\vec{OA}\)反向,每块多边形外的面积一定会被抵消
因此,对于一个多边形A,其顶点一次为{\(A_1,A_2...A_n\)},其面积公式为:
凸包
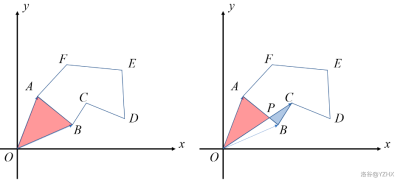
所谓凸包,就是在最小化周长的情况下,一个能将所有给定的点都覆盖的图形。
如下图:左图不是凸包,而改成右图后就成了凸包
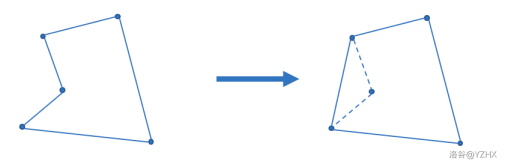
凸包由逆时针方向遍历,每条边与下一条边的叉积一定为正
(由此可以求出凸包)
求凸包
这里分享一下一次性求出整个凸包的方法:
- 以(y,x),找到最小的点
- 以该点建立极坐标系(即将该点当做(0,0))
- 将剩下的点按 (极角,极径)排序
- 利用相邻边叉积为正的性质,单调栈维护
(脑补一下画面,很好理解)
bool cmp(vec a,vec b){return a*b==0 ? dis(a) < dis(b) : a*b>0; }
void convexhull()
{
for(int i=n; i>=1; --i) a[i]=a[i]-a[1];
sort(a+2,a+n+1,cmp);
for(int i=1;i<=n;++i) {
st[++top]=a[i];
while(top>2 && (st[top-1]-st[top-2])*(st[top]-st[top-1])<0) st[top-1]=st[top], top--;
}
}
判断点是否在凸包内
将点A,加入上面的方法建立的极坐标系,lower_bound得到极角排序后在它之前与在它之后的,然后跨立实验即可
旋转卡壳
如何求平面上的最远点对?
思路:
不难发现,平面上的最远点对一定存在于凸包上(画图很好理解)。
凸包上,距离点A最远的点B,那么离A最远的边,一定以B为端点。
换句话说,若能确定凸包上某条边与某个点相距最远,则最远的点对一定是该点与边的某个端点
感性理解一下: 若以该点向边作垂线,连端点,端点于该点连线一定是斜边,斜边大于直角边
如何找到离每条边最远的点(对踵点)呢?
用选定的边做平行直线,恰好接触到凸包时,平行线与凸包的交点就是了
而凸包上边的斜率变化是单调的, 因此不难发现对踵点的位置也是单调的
即:随着逆时针选取边,其对踵点也会逆时针旋转
Code
db dis_line(vec a,vec b,vec c) { return (b-a)*(c-a)/(b-a).dis(); }//点C到直线AB的距离
ll qiaqiao()
{
if(top==1) return 0;
if(top==2) return (st[1]-st[2]).dis();
st[1+top]=st[1]; //便于找边
int j=1; db ans=0;//j记录对踵点
for(re int i=1;i<=top;++i) {
while(dis_line(st[i],st[i+1],st[j])<dis_line(st[i],st[i+1],st[j+1])) j=j%top+1;
ans=max(ans, max((st[i]-st[j]).dis(), (st[i+1]-st[j]).dis()));
}
return ans;
}
半平面交
常见应用
- 多边形面积交
- 多边形的核
(能在该区域“看到”多边形内部的每个角落) - 求解二元一次不等式组
算法本质
求解由二元一次不等式组的可行解
例题:射箭
如多条直线\(l_i: A_ix+B_iy+C_i\geq0\) 所包含的面积
因为,\(A_ix+B_iy+C_i\geq0\) 类似的不等式,其中合法的(x,y)只能是这条直线的一个半平面.
对于不等式到半平面交中的转化:
(以求直线左侧半平面交为例)
- 若\(l_i: A_ix+B_iy+C_i\geq0\), 则把直线的方向与x轴相同,若是垂直与x轴,方向竖直向上
- 若\(l_i: A_ix+B_iy+C_i\leq0\), 则把直线的方向与x轴相反,若是垂直与x轴,方向竖直向下
算法思路
以逆时针方向为正,则所有边的左边部分都是可能保留的半平面,多个图形的所有边的半平面的交集即为多边形面积交,单个图形的半平面交为多边形的核
具体求法如下:
- 将所有线段按方向向量的极角排序
- 将所有线段一次插入双端队列:
- 比较新加入的边是否遮盖队头,是则弹出队头
- 比较新加入的边是否遮盖队尾,是则弹出队尾
- 最后检查队列的头尾是否能遮盖
注:
- 极角排序过程中,若有两线段平行(极角相同),保留更靠左的那条(靠左的遮盖了靠右的)
- 上述中的遮盖,指的是:若a能遮盖b,则双端队列中有了a,即使去除b后半平面交也不会有变化
关于遮盖与否的判断方式:
若待加入的线段a与倒数第二个线段c的交点在最后两个线段b,c的交点的左边,则代表线段a在半平面交中能完全替代线段b
Code
struct line{
vec st, ed, c;//c是st->ed的向量
bool operator <(const line l)const {
db A=atan2(c.y,c.x), B=atan2(l.c.y,l.c.x);
if(fabs(A-B)>eps) return A<B;
return c*(l.ed-st)<0;
}
}l[_*_], qwe[_*_];
vec intersection(line l1,line l2) //两直线求交
{
vec st1=l1.st, st2=l2.st;
vec a=l1.c, b=l2.c, c=st2-st1;
if(fabs(b*a)<eps) return vec(-1e12,-1e12);
return st1+(a^((b*c)/(b*a)));
}
int n, m, hd, tl;
line q[_*_];
bool check(line a,line b,line c)
{//通过叉积来比较b,c交点与a向量的左右关系,进而推出线段是否遮盖
vec p=intersection(b,c);
return (a.c*(p-a.st))+eps<=0;
}
in void solve(int cnt)
{
int tot=0;
sort(l+1,l+cnt+1); qwe[++tot]=l[1];
for(re int i=2;i<=cnt;++i)
{
if(fabs(atan2(l[i].c.y,l[i].c.x)-atan2(l[i-1].c.y, l[i-1].c.x))<eps) continue;
qwe[++tot]=l[i];
} //去重
for(re int i=1;i<=tot;++i) l[i]=qwe[i];
m=tot;
for(re int i=1;i<=m;++i) //双端队列维护
{
while(tl>hd && check(l[i], q[tl], q[tl-1])) tl--;
while(tl>hd && check(l[i], q[hd], q[hd+1])) hd++;
q[++tl]=l[i];
}
while(tl>hd && check(q[tl], q[hd], q[hd+1])) hd++;
while(tl>hd && check(q[hd], q[tl], q[tl-1])) tl--;
}
最小圆覆盖
算法流程
- random_shuffle
- 枚举第一个点i作为圆心
- 从 \([1,i)\) 中枚举j, 并以 \(ij\) 作为直径
- 从 \([1,j)\) 中枚举k,并找到 \(\triangle_{ijk}\) 的外接圆
找外接圆,可以通过三角形两边的中垂线的交点
在上述234过程中不断维护最小圆的圆心和半径,若一个点已在当前圆内,则跳过它
Code(LG模板)
#include<bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
#define get getchar()
#define in inline
#define db long double
const int _=2e5+23;
const db eps = 1e-15;
int n;
struct vec{
db x,y;
vec(){x=y=0;}
vec(db a,db b){x=a, y=b;}
vec operator+(const vec b)const{return vec(x+b.x,y+b.y);}
vec operator-(const vec b)const{return vec(x-b.x,y-b.y);}
vec operator/(const db b)const {return vec(x/b, y/b);}
db operator*(const vec b)const{return x*b.y-y*b.x;}
vec operator^(const db b)const{return vec(x*b, y*b);}
db dis(){ return sqrt(x*x+y*y);}
vec rot(){ return vec(-y,x);}
}a[_];
vec intersection(vec p,vec a,vec q,vec b) //p是点,a是从p出发的向量,q、b同理
{
vec c=(q-p);
return p+(a^((b*c)/(b*a)));
}
vec getcircle(vec A,vec B,vec C)//找到三角形abc的外接圆圆心
{
return intersection((A+B)/2,(B-A).rot(),(C+A)/2,(C-A).rot());
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i) scanf("%Lf%Lf", &a[i].x, &a[i].y);
if(n==1) { cout<<0<<endl<<a[1].x<<' '<<a[1].y<<endl; return 0; }
vec o; db R=0;
for(re int i=2;i<=n;++i)
{
if((a[i]-o).dis()<=R) continue;
o=a[i];
for(re int j=1;j<i;++j)
{
if((a[j]-o).dis()<=R) continue;
o=(a[j]+a[i])/2; R=(o-a[i]).dis();
for(re int k=1;k<j;++k)
{
if((a[k]-o).dis()<=R) continue;
o=getcircle(a[i],a[j],a[k]); R=(o-a[i]).dis();
}
}
}
printf("%.10Lf\n%.10Lf %.10Lf\n",R,o.x,o.y);
return 0;
}
附赠上述所有模板(除半平面交,圆覆盖)
#include<bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
#define get getchar()
#define in inline
in int read()
{
int t=0, x=1; char ch=get;
while(ch!='-' && (ch<'0' || ch>'9')) ch=get;
if(ch=='-') ch=get, x=-1;
while(ch<='9' && ch>='0') t=t*10+ch-'0', ch=get;
return t*x;
}
#define db double
const int _=1e5+23;
const db inf=1e9, pi = acos(-1), eps=1e-10;
struct vec{//存储向量或者点坐标
db x,y;
vec(){x=y=0;}
vec(db a,db b){x=a,y=b;}
vec operator+(const vec b) const{ return (vec){x+b.x, y+b.y}; }
vec operator-(const vec b) const{ return (vec){x-b.x, y-b.y}; }
db operator*(const vec b) const{ return x*b.y-y*b.x; } //叉积
db operator&(const vec b) const{ return x*b.x+y*b.y; } //点积
vec operator^(const db b) const{ return (vec){x*b,y*b}; } //数乘
db dis(){ return sqrt(x*x+y*y);} //向量模长/距离
};
bool cmp(vec a,vec b){return a*b==0 ? a.dis()<b.dis() : a*b>0;}//极角排序
vec st[_]; int top;
void convexhull(vec *a,int n)//求凸包
{
for(int i=n;i>=1;--i) a[i]=a[i]-a[1];
sort(a+2,a+n+1,cmp); top=0;
for(int i=1;i<=n;++i) {
st[++top]=a[i];
while(top>2 && (st[top-1]-st[top-2])*(st[top]-st[top-1])<0) st[top-1]=st[top], top--;
}
}
in db dis_line(vec a,vec b,vec c) { return (b-a)*(c-a)/(b-a).dis(); }//点到直线的距离
in ll qiaqiao() //旋转卡壳(凸包直径)
{
if(top==1) return 0;
if(top==2) return (st[1]-st[2]).dis();
st[1+top]=st[1]; int j=1; db ans=0;
for(re int i=1;i<=top;++i)
{
while(dis_line(st[i],st[i+1],st[j])<dis_line(st[i],st[i+1],st[j+1])) j=j%top+1;
ans=max(ans, max((st[i]-st[j]).dis(), (st[i+1]-st[j]).dis()));
}
return ans;
}
bool iscross(vec a,vec b,vec c,vec d) //ab,cd两线段是否相交
{
if(((a-c)*(d-c))*((d-c)*(b-c))<0) return 0;
if(((c-a)*(b-a))*((b-a)*(d-a))<0) return 0;
return 1;
}
vec crossover(vec A1,vec A2,vec B1,vec B2) //A1A2,B1B2两直线交点
{
vec a=(A2-A1), b=(B2-B1), c=(B1-A1);
if(fabs(a*b)<eps) return (vec){-inf,-inf}; //两直线平行
return A1+(a^((b*c)/(b*a)));
}
db getarea(vec *A,int n) //求以A点集为顶点的多边形面积
{
db s=(A[n]*A[1])/2.000;
for(re int i=1;i<n;++i) s+=(A[i]*A[i+1])/2.000;
return fabs(s);
}
int main()
{
return 0;
}