红黑树代码实现

// 这里JDK中TreeMap红黑树自平衡的代码

private void fixAfterInsertion(TreeMap.Entry<K, V> x) {
    // 新增节点,直接置为RED
    x.color = RED;
    
    // 父节点是红色
    while (x != null && x != root && x.parent.color == RED) {
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {  // 父节点是爷结节的左子节点
            TreeMap.Entry<K, V> y = rightOf(parentOf(parentOf(x))); // x的右叔
            if (colorOf(y) == RED) { // 右叔是红色
                setColor(parentOf(x), BLACK);  // 父置为黑色
                setColor(y, BLACK);  // 叔置为黑色
                setColor(parentOf(parentOf(x)), RED); // 爷置为红色
                x = parentOf(parentOf(x));  // 将爷结点置为当前活动节点
            } else {
                if (x == rightOf(parentOf(x))) { // x是父节点右子结点
                    x = parentOf(x);    //将父节点置为当前活动节点, 为左旋做准备
                    rotateLeft(x);  // 左旋
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {  // 父节点是爷结点的右子节点
            TreeMap.Entry<K, V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

/**
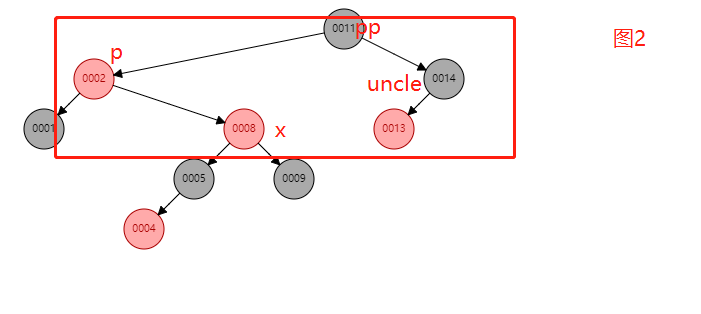
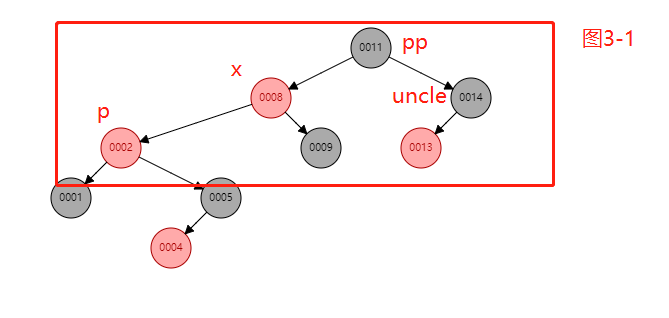
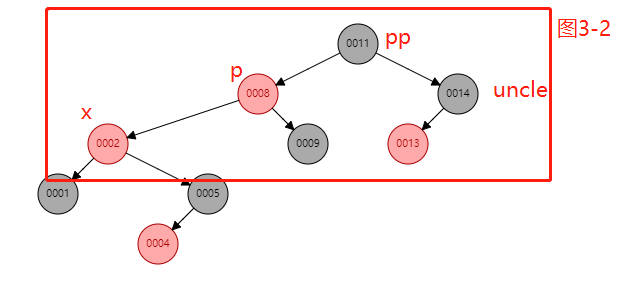
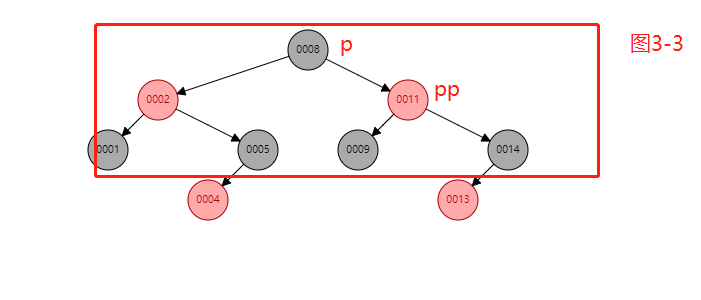
 * 红黑树
 */
class RBNode<T extends Comparable<T>> {
    boolean red = true;
    T data;
    RBNode<T> left;
    RBNode<T> right;
    RBNode<T> parent;

    public RBNode(boolean red, T data, RBNode<T> left, RBNode<T> right, RBNode<T> parent) {
        this.red = red;
        this.data = data;
        this.left = left;
        this.right = right;
        this.parent = parent;
    }


    public RBNode(T data) {
        this.data = data;
    }

    /**
     * 返回当前节点的root节点
     * 该方法的时间复杂度应该是O(n)
     *
     * @return
     */
    final RBNode<T> root() {
        for (RBNode<T> root = this, p; ; ) {
            if ((p = root.parent) == null) {  // 如果当前节点的父节点为空,那说明当前节点就是根节点,直接返回当前节点
                return root;
            }
            root = p;  // 当前节点变成原节点的父节点
        }
    }


    /*
     * 左旋示意图：对节点x进行左旋
     *     p                       p
     *    /                       /
     *   x                       y
     *  /                      / 
     *lx   y      ----->       x   ry
     *    /                  /  
     *  ly   ry              lx   ly
     * 左旋做了三件事：
     * 1. 将y的左子节点赋给x的右子节点,并将x赋给y左子节点的父节点(y左子节点非空时)
     * 2. 将x的父节点p(非空时)赋给y的父节点，同时更新p的子节点为y(左或右)
     * 3. 将y的左子节点设为x，将x的父节点设为y
     * 注意: 在移动节点位置时,不要忘了双向指定
     */
    public void rotateLeft(RBNode<T> x) {
        RBNode<T> y, ly, p;
        if (x != null && (y = x.right) != null) {
            // 1.  将y的左子节点赋给x的右子节点,并将x赋给y左子节点的父节点(y左子节点非空时)
            // 做非空的判断的目的是: 如果y没有左子节点,都不用挂到x的右子节点上了
            if ((ly = x.right = y.left) != null) {
                ly.parent = x;
            }

            //2. 将x的父节点p(非空时)赋给y的父节点，同时更新p的子节点为y(左或右)
            if ((p = y.parent = x.parent) == null) {
                y.parent = null;// y成了根节点,可以直接置为黑色
                y.red = false;
            } else if (p.left == x) {  // 如果x是p的左子节点,那么旋转后y也是p的左子节点
                p.left = y;  // 将y置为p的左子节点
            } else {     // x是p右子节点,那么旋转后y也是p的右子节点
                p.right = y;  // 将y置为p的右子节点
            }

            // 3. 将y的左子节点设为x，将x的父节点设为y
            y.left = x;
            x.parent = y;
        }
    }


    /*
     * 右旋示意图：对节点y进行右旋
     *        p                   p
     *       /                   /
     *      y                   x
     *     /                  / 
     *    x   ry   ----->    lx   y
     *   /                      / 
     * lx   rx                 rx   ry
     * 右旋做了三件事：
     * 1. 将x的右子节点赋给y的左子节点,并将y赋给x右子节点的父节点(x右子节点非空时)
     * 2. 将y的父节点p(非空时)赋给x的父节点，同时更新p的子节点为x(左或右)
     * 3. 将x的右子节点设为y，将y的父节点设为x
     */
    public void rotateRight(RBNode<T> y) {
        RBNode<T> x, rx, p;
        if (y != null && (x = y.left) != null) {

            // 1. 将x的右子节点赋给y的左子节点,并将y赋给x右子节点的父节点(x右子节点非空时)
            if ((rx = y.left = x.right) != null)
                rx.parent = y;

            // 2. 将y的父节点p(非空时)赋给x的父节点，同时更新p的子节点为x(左或右)
            // 2. 简而言之, 就是挂左挂右的问题
            if ((p = x.parent = y.parent) == null) {  // 判断父是否为null
                x.parent = null;
                x.red = false;  // 这句代码放这儿好吗?
            } else if (p.right == y) {  // 判断是左...
                p.right = x;
            } else {   // 否则就是右
                p.left = x;
            }

            // 3. 将x的右子节点设为y，将y的父节点设为x
            x.right = y;
            y.parent = x;
        }
    }

    /**
     * 从root节点开始遍历比较
     *
     * @param x
     */
    public void insert(RBNode<T> x) {
        RBNode<T> root = root();
        insert(root, x);
        // todo 重平衡...
        balanceInsertion(x);
    }

    /**
     * 有如下多种情况:
     * 1. 如果原树为空, root == x, 只需要把root置为黑色即可
     * 2. 如果父节点是黑色,添加上去即可,啥都不需要做
     * 3. 下面三种情况较为复杂,需要变色或者旋转
     * (1).插入节点的父节点和其叔叔节点（祖父节点的另一个子节点）均为红色的；
     * (2).插入节点的父节点是红色，叔叔节点是黑色，且插入节点是其父节点的右子节点；
     * (3).插入节点的父节点是红色，叔叔节点是黑色，且插入节点是其父节点的左子节点。
     *
     * @param x
     */
    private void balanceInsertion(RBNode<T> x) {
        RBNode<T> p, pp;
        // 1.如果原树为空, root == x, 只需要把root置为黑色即可
//        if (x.parent == null) {
//            x.red = false;
//        }
        //2. 如果父节点是黑色,添加上去即可,啥都不需要做
        // todo : 还存在bug,就是链表的情况,待完善
        //3. 父节点是红色
        while ((p = x.parent) != null && p.red) {// 结束条件就是x.parent == null . 只有根节点才满足此条件
            pp = p.parent;// 爷节点, 如果父是红,肯定有爷节点
            //  8 ----> 11---->14----->13----->1---->2-----> 5----->9  ----> x= 4
            if (p == pp.left) {  // 父节点是爷节点左子节点
                // 获取叔节点,因为父是左,叔肯定是右
                RBNode<T> uncle = pp.right;
                // 第1种情况,叔节点是红色-------> 可参考图1
                if (uncle != null && uncle.red) {
                    p.red = false;// 父置黑
                    uncle.red = false;// 叔置黑
                    pp.red = true;// 爷置红
                    x = pp;// 将爷节点置为活动节点
                    continue;// 继续进行判断
                }

                // 2.第2种情况,叔是黑色, 当前节点x是右子节点-------> 参考图2
                if (x == p.right) {
                    // 左旋, 注意中心点是当前节点的父节点
                    rotateLeft(p);  // 左旋之后,参考图3-1
                    // 好好体会这个三行代码, 太有技术含量了....
                    RBNode<T> temp = p;
                    p = x;
                    x = temp;// 交换之后,参考图3-2
                }
                //3. 第3种情况,叔是黑, 当前节点x是左子节点
                p.red = false;
                pp.red = true;
                rotateRight(pp);  //参考图3-3
            } else {// 父节点是爷节点右子节点, 与上面相反了.
                RBNode<T> uncle = pp.left;

                // 1. 第一种情况uncle是红色
                if (uncle != null && uncle.red) {
                    p.red = false;// 父置黑
                    uncle.red = false;// 叔置黑
                    pp.red = true;// 爷置红
                    x = pp;// 将爷节点置为活动节点
                    continue;// 继续进行判断
                }

                //第2种情况,uncle节点是黑色的，且当前节点是左子节点
                if (x == p.left) {
                    rotateRight(p);
                    RBNode<T> tmp = p;
                    p = x;
                    x = tmp;
                }

                //第3种情况,uncle节点是黑色的，且当前节点是右子节点
                p.red = false;
                pp.red = true;
                rotateLeft(pp);
            }
        }
        // 根弄黑
        RBNode<T> root = root();
        root.red = false;
    }

    private void insert(RBNode<T> root, RBNode<T> x) {
        if (root.data.compareTo(x.data) < 0) {
            if (root.right == null) {
                root.right = x;
                x.parent = root;
            } else {
                insert(root.right, x);
            }
        } else {
            if (root.left == null) {
                root.left = x;
                x.parent = root;
            } else {
                insert(root.left, x);
            }
        }
    }

    public void preOrderTraversal(RBNode<T> root) {
        if (root == null) {
            return;
        }
        System.out.println(root.toString());
        preOrderTraversal(root.left);
        preOrderTraversal(root.right);
    }

    @Override
    public String toString() {
        return "red=" + (red ? "Red" : "Black") + ", data=" + data;
    }
}

未完待续中......