JAVA笔记整理-集合框架-单链表-队列结构-栈结构

一、集合框架

有关LinkedList的集合的，它是一个链表结构的集合

1、链表结构

1.1 单链表的结构

所谓单链表（Linked）在内存中不连续的一端内存空间， 链表的每一个元素是一个节点，每一个结点由数据元素和下一个结点的存储位置组成，链表结构与数组结构最大区别是链接结构的存储内存是不连续的，而数组结构的内存是连续的，链表结构不能与数组结构一样快速查找，

​ 链表结构操作特点是 添加，删除元素效率高，查询效率低；

​ 数组结构操作特点： 添加，删除效率低，查询效率高

前驱： 该节点的上一个元素的地址

后继： 该节点的下一个元素的地址

链表结构中最后一个元素的”后继“为null

1.2 单链表的实现

链表实现添加元素：

  /**
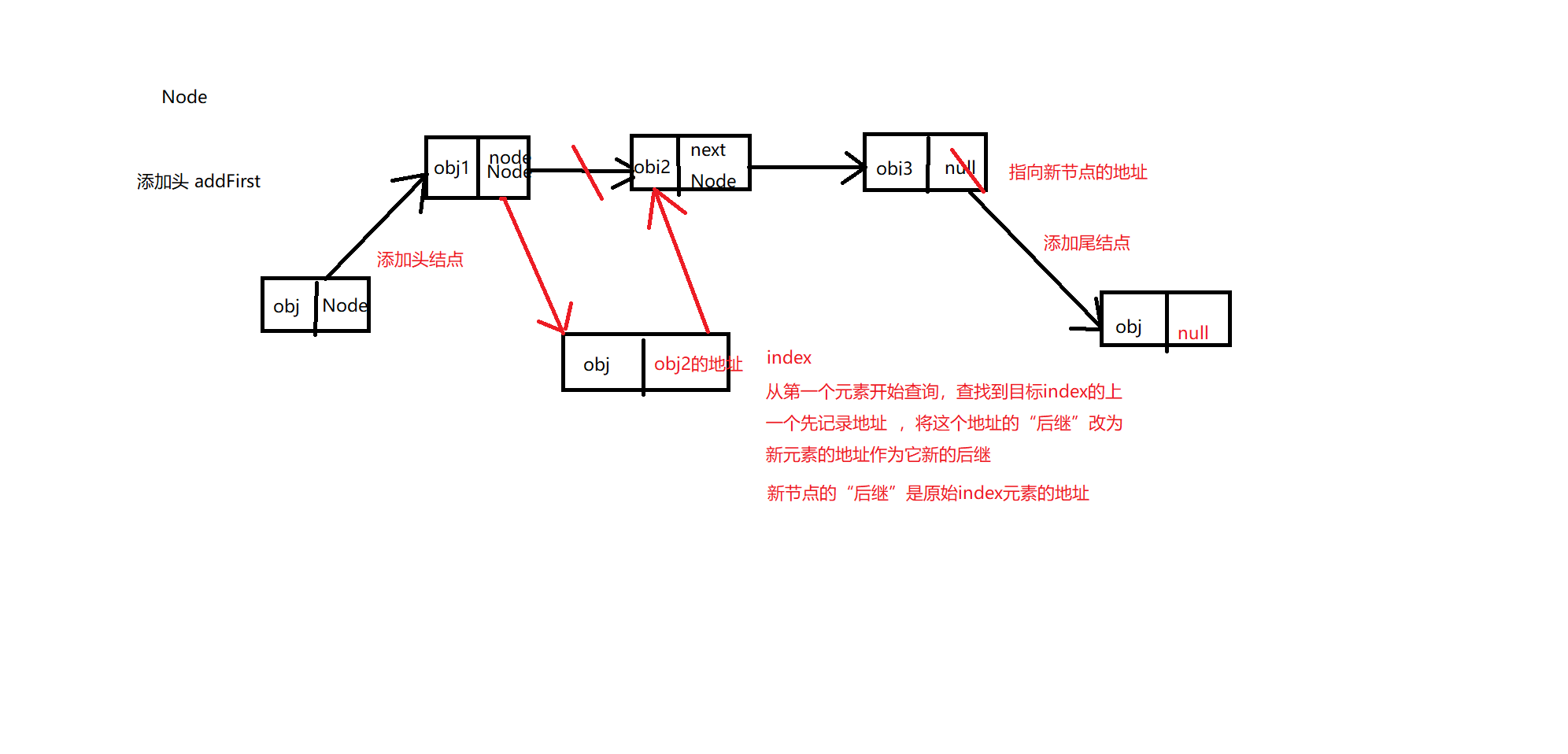
     * 添加到最后元素
     * @param obj
     */
     public void addLast(Object obj){
         //将节点添加到最后
         //add(obj , this.size);
         // 创建节点
//         Node node = new Node(obj);
//         // 找到最后一个元素的地址
//         Node lastNode = this.header;
//         for(int i = 0;i<this.size-1 ;i++){
//             lastNode  = lastNode.next;
//         }
//
//           lastNode.next=node;
         // 找最后一个结点 （由于最后一个结点的next是null）
         Node node = new Node(obj);
           Node lastNode = this.header;
           while(lastNode.next!=null){
               lastNode = lastNode.next;
           }
           lastNode.next = node;

           this.size++;

     }

  /**
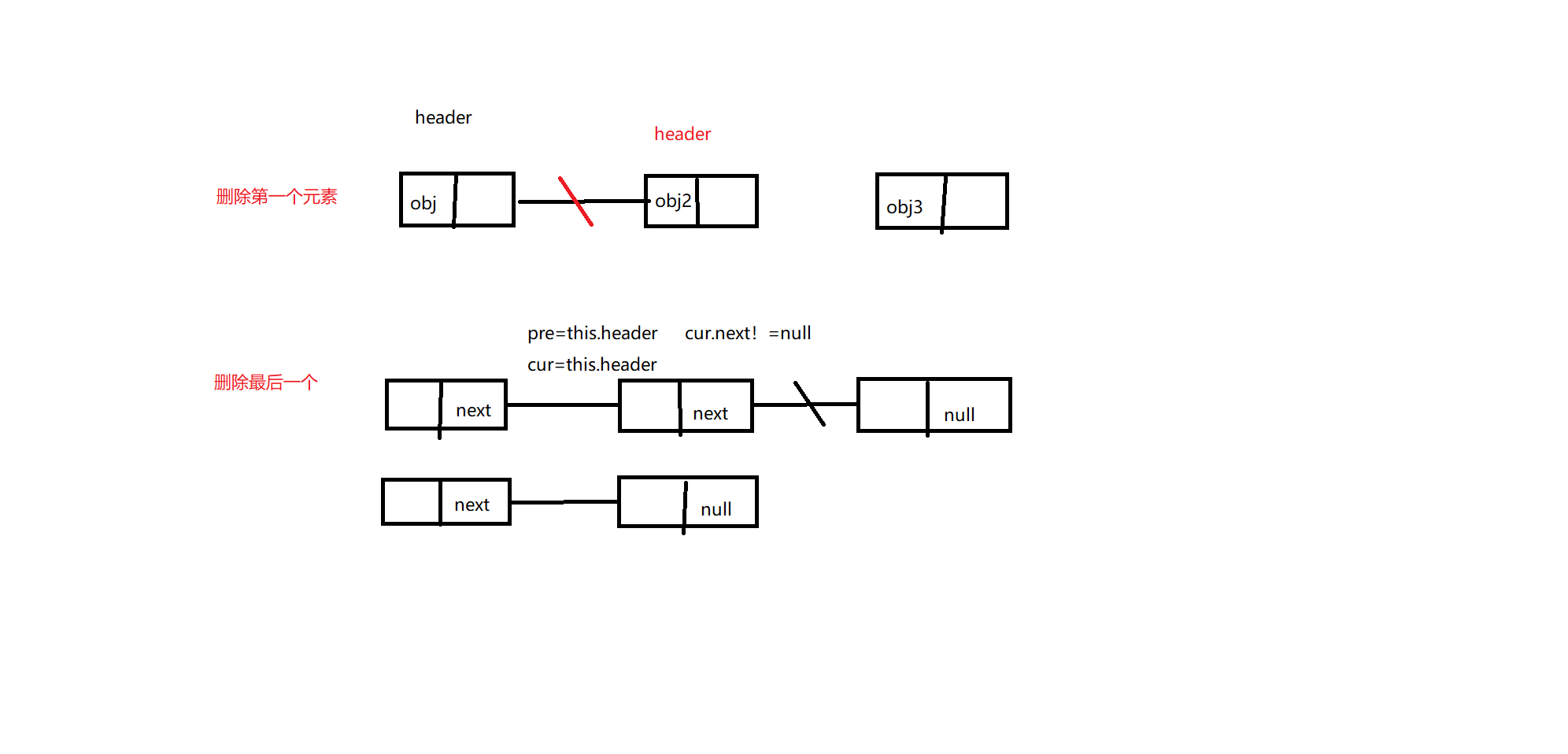
     * 删除第一个节点
     * @param index
     * @return
     */
    public void removeFirst(){
        //删除第一个节点
        if(this.size==0){
            throw new IllegalArgumentException("没有需要删除的原始");
        }
        //  获取当前连接的“后继”
        Node node =  this.header.next;
        // 并让后继作为头
        this.header = node;
        this.size--;
    }

    /**
     * 删除最后节点
     */
    public void removeLast(){
        //删除是否存在数据
        if(this.size==0){
            throw new IllegalArgumentException("没有需要删除的原始");
        }
        // 找最后一个元素的前一个 地址   ，并将该地址的next 改为null
        Node cur  = this.header;
        Node pre = this.header;
        while(cur.next!=null){
               pre = cur;
                // 下一个变为当前
               cur =  cur.next;
        }
         // 最后一个元素  就是 当前
        pre.next = null;
        size--;
    }

单链练习：整体
package linked;

import javax.xml.soap.Node;

/**
 * @ClassName:JAVA
 * @Author:ZhouHongTing
 * @pate:2020/10/26 18:47
 * @Description;
 */
public class Test<T> {
    //创建链表头部
     Node header; //如果有节点，那么这就是头节点
    int size;//计算链表数量

    //创建节点类
    class Node<T>{
        //节点内容
        T data;
        Node next;//下一个节点地址
        public Node(T data){
            this.data=data;
        }
        //获取data
        public T getData(){
            return data;
        }
        //设置data
        public void setData(T data){
            this.data=data;
        }
        //获取下一个节点地址
        public Node next(){
            return next;
        }
        //设置下一个节点地址
        public void setNext(){
            this.next=next;
        }
    }
    /**
     * 将元素添加到第一个节点
      */
    public void addFirst(T n){
        //创建节点
        Node node=new Node(n);
        node.next=this.header;//新节点的后继就是原节点头部
        this.header=node;//将头节点变为新要添加的节点
        //节点计数器加一
        size++;
    }
    /**
     * 添加到最后元素
     */
    public void addLast(T n){
        //创建新节点
        Node node=new Node(n);
       Node lastNode=this.header;//创建一个最后节点，赋予头值从头开始算，求出最后节点
       while (lastNode.next!=null){
           lastNode=lastNode.next;
       }
       lastNode.next=node;
       this.size++;
    }
    /**
     * 插入一个指定下标节点
     */
    public void addIndex(T n,int index){
     Node node=new Node(n);//创建新节点

     Node cle=this.header;//创建 一个前节点获取头节点值作为初始值
        Node cur;//创建一个后一个节点，装前一个节点的（下一个节点地址）
        for(int i=0;i<index-1;i++){
            cle=cle.next;//循环判断到指定下标的前一个节点
        }
        cur=cle.next;//将前一个节点的下个节点地址存入
        cle.next=node;//前一个节点的下一个节点地址就是当前插入元素节点
        node.next=cur;//当前节点的下个节点位置就是原先前节点的下个节点地址
        this.size++;
    }
    /**
     * 删除第一个节点
     */
    public void removeFirst(){
        //先判断是否存在节点
        if(this.size==0){
            throw new IllegalArgumentException("没有需要删除的节点");
        }
        //获取当前节点的"后继"
        Node node=this.header.next;//获取当前头节点的后继节点
        //让后继节点替换头节点便完成删除头节点
        this.header=node;
        this.size--;
    }
    /**
     *删除一个指定下标节点
     */
    public void removeIndex(int index){
    //    Node node=new Node(n);
        if(this.size<index){
            throw new IllegalArgumentException("要删除的节点不存在");
        }
        Node pre=this.header;
        Node cur=this.header;
        for(int i=0;i<index;i++){
            pre=cur;
            cur=pre.next;
        }
        pre.next=cur.next;
        this.size--;
    }
    /**
     * 删除最后节点
     */
    public void removeLast(){
        //判断是否存在节点
        if(this.size==0){
            throw new IllegalArgumentException("没有节点");
        }
        //找到最后一个节点的前一个节点，并将它下个节点地址改为null
        Node cur=this.header;
       // Node pre=header;
        while (cur.next!=null){
          //  pre=cur; //获取的后继节点就是下一个节点
            cur=cur.next;//获取节点后继，直到cur.next=null
        }
      //  pre.next=null;
        cur.next=null;
        this.size--;

    }

    /**
     * 根据下标获取节点
     * @param
     */
    public Node getShowInfo(int index){
        //判断是否为空节点
        if(this.size==0){
            throw new IllegalArgumentException("这是空节点");
        }
        if(index==0){
            return this.header;
        }
        //查找指定下标的元素
        Node cur=this.header;//从第一个元素开始
        int j=0;
        while (index!=j&&index<this.size){
            cur=cur.next;
            j++;
        }
        return cur;
    }
    //测试
    public static void main(String[]args){
        Test test=new Test();
        test.addFirst("hello1");
        test.addFirst("hello2");
        test.addFirst("hello3");
        for(int i=0;i<test.size;i++){
            System.out.println(test.getShowInfo(i).getData());//输出添加的节点元素
        }
        test.addIndex("hello",1);//在指定位置添加节点元素   
        System.out.println(test.size);  //查看节点数量     //4
        test.removeFirst();   //删除第一个节点元素
        System.out.println(test.header.getData());        //hellio
        test.removeLast(); //删除最后一个节点元素             
        System.out.println(test.size);                  //2
        System.out.println(test.getShowInfo(test.size-1).getData());//hello2
        test.removeIndex(1); //删除指定下标为1 的节点元素
        System.out.println(test.size);  //1
        System.out.println(test.getShowInfo(1).getData());  //hello
    }
}

2、队列结构

队列结构（Queue）： 在基于链表结构的基础上 ，实现的一种“先进先出”的结构， 常用操作 入队（put），出队（pop） ，设置队列的头结点 和 尾结点

package com.j2008.dataStruct;

public class MyQueue<T> {
    // 头结点
    private Node front;
    //  尾结点
    private Node tail;
    // 大小
    private int size;

    public MyQueue(){
        //  头，尾为空
        this.front= this.tail=null;
    }

    class Node{
        private T obj;
        private Node next;
        public Node(T obj){
            this.obj = obj;
        }

        public T getObj() {
            return obj;
        }

        public void setObj(T obj) {
            this.obj = obj;
        }

        public Node getNext() {
            return next;
        }

        public void setNext(Node next) {
            this.next = next;
        }
    }

    /**
     * 入队 ： 将元素添加到队列的尾部
     */
    public void put(T obj){
        // 创建节点
        Node node = new Node(obj);
        // 如果元素为空 则头就尾，尾就是头
        if(isEmpty()){
            this.front = this.tail = node;
            return ;
        }
        // 将新元素的地址 作为尾的next
        this.tail.next=node;
        //将新元素的结点 作为尾节点
        this.tail = node;

        this.size++;
    }

    /**
     * 出队： 将元素从队列的头部移除 （保持与队列脱离关系）
     * @return
     */
    public T pop(){
        if(isEmpty()){
            throw new IllegalArgumentException("没有可出队的元素");
        }
        // 移除头部元素
        Node popNode = this.front;
        // 设置现在的头元素是下一个
        this.front = popNode.next;
        //  将弹出的元素next 设置null，与队列脱离关系
        popNode.next=null;
        this.size--;
        // 如果没有元素了 则需要 设置头尾都是null
        if(this.size<0){
            this.front=this.tail=null;
        }
        return  popNode.getObj();
    }

    /**
     * 判断元素是否为空
     * @return
     */
    public boolean isEmpty(){
        if(this.front==null && this.tail==null){
            return true;
        }
        return false;
    }

}

队列结构整体练习：

package linked;

/**
 * @ClassName:JAVA
 * @Author:ZhouHongTing
 * @pate:2020/10/27 9:08
 * @Description;
 */
public class Test2<T> {
    //创建头部结点
   private Node front;
    //创建尾部结点
   private Node tail;
    //创建结点计数器
    int size=0;
    public class Node{
        //创建结点元素，装纳内容
        private  T Info;
        //创建下一个节点地址对象
        Node next;

        public Node(T info) {
            this.Info = info;
        }

        public T getInfo() {
            return Info;
        }

        public void setInfo(T info) {
            this.Info = info;
        }
    }
    /**
     * 入队
     */
    public void put(T t){
        Node node=new Node(t);
        //判断结点是否为空
        if(isEmpty()){
            front=tail=node;  //若都为空，则添加的元素，遵循先进先出，即尾就是头；
        }
        //若不为空，则新添加的节点元素为尾
        tail.next=node;
        tail=node;
        size++;
    }
    /**
     * 出队
     */
    public void out(){
        //判断有无结点
       if(isEmpty()){
           throw new IllegalArgumentException("结点为空");
       }
        //若不为空，则从头开始出队，即删除头部元素
        Node node=front;//获取头结点元素
        front=node.next;//将头结点下个结点地址，重新赋值给头结点，即原来的头结点被它的下一个结点覆盖
        //将获取的头结点与队列断开联系，即出队,即设置它的下个结点地址为空
        node.next=null;
        size--;
        //当计算器为0时，则头尾皆空
        if(this.size<=0){
            front=tail=null;
        }
    }

    /**
     * 判断结点是否为空
     */
    public boolean isEmpty(){
        if(front==null&&tail==null){
            return true;
        }
        return false;
    }

    /**
     * 测试
     */
    public static void main(String[] args) {
        Test2 t=new Test2();
        //入队
        t.put("hello1");
        t.put("hello2");
        t.put("hello3");
        //输出结点数量
        System.out.println(t.size);//3
        //输出头结点元素
        System.out.println(t.front.Info);//hello
        //输出尾结点元素
        System.out.println(t.tail.Info);//hello3
        //出队
        t.out();
        System.out.println(t.size);//2
        //输出头结点元素
        System.out.println(t.front.Info);//hello2
        //输出尾结点元素
        System.out.println(t.tail.Info);//hello3

    }
}

3、栈结构

栈（Stack）结构也是常用数据结构之一，它具有 “后进先出” 的特点

public class MyStack<T> {
    // 定义一个数组 ，用于存储元素
    private Object[] obj;
    private int size;
    public MyStack(){
        obj = new Object[10];
        size=0;
    }

    /**
     * 入栈： 压入栈顶元素
     * @param t
     */
    public void push(T t){
        expandCapacity(size+1);
        obj[size]=t;
        size++;
    }

    /**
     *  返回栈顶元素：peek
     */
    public T peek(){

        if(size>0) {
            return (T) obj[size - 1];
        }
        return  null;
    }

    /**
     * 出栈： 返回栈顶的元素，并删除该元素
     * @return
     */
    public T pop(){
        T t = peek();
        if(size>0) {
            // 将最后一个元素 删除
            obj[size - 1] = null;
            size--;
        }
        return t;
    }

    /**
     * 是否为空元素
     * @return
     */
    public boolean  isEmpty(){
        return  size==0;
    }
    /**
     * 扩容数组大小 ： 扩容1.5倍
     */
    public void expandCapacity(int size){
        if(obj.length< size){
            // 需要扩容
            int length = size*3/2 + 1;
           this.obj =  Arrays.copyOf(this.obj,length);
        }
    }

}

链表实现栈结构练习：

package linked;

/**
 * @ClassName:JAVA
 * @Author:ZhouHongTing
 * @pate:2020/10/27 9:53
 * @Description;
 */
public class Test3<T> {
    //创建头部结点
    private Node head;
    //创建结点计数器
    int size;
    //创建结点
    public class Node{
        //创建内容变量
       private T Info;
       //创建下个结点地址对象
        Node next;

        public Node(T info) {
            Info = info;
        }

        public T getInfo() {
            return Info;
        }

        public void setInfo(T info) {
            Info = info;
        }
    }
    /**
     * 入栈
     */
    public void put(T t){
        //创建新结点元素
        Node node=new Node(t);
        //每装入一个新结点，都为头结点
        //创建一个结点来装纳头结点，然后交换
        Node next=head;
        head=node;     //将新结点设置为头部结点
        head.next=next;  //将原头结点，设置为现在的头结点的下一个结点地址
        size++;
    }
    /**
     * 出栈
     */
    public void out(){
        //入栈出栈，先进后出
        //判断是否为空结点
        if(size==0){
            throw new IllegalArgumentException("结点为空");
        }
        //创建一个结点来装入头部结点，出栈的第一个元素
        Node node=head;
        head=node.next; //将头结点的下一个结点地址元素设置为新的头部
        //设置原先头结点的下个结点地址为空，切断与栈的练习，出栈
        node.next=null;
        size--;
    }
    /**
     * 输出指定下标结点元素
     */
    public Node showInfo(int index){
        //判断是否为空
        Node pre=this.head;
        if(index<0||index>=size){
            throw new IllegalArgumentException("没有结点");
        }
        for(int i=0;i<index;i++){
            pre=pre.next;
        }
        return pre;
    }
    /**
     * 测试
     */
    public static void main(String[] args) {
        //入栈
        Test3 t=new Test3();
        t.put("hello1");
        t.put("hello2");
        t.put("hello3");
        t.put("hello4");
        //测试
        for (int i=0;i<t.size;i++){
            System.out.println(t.showInfo(i).Info);  
        }
        //出栈
        t.out();
        t.out();
      //  System.out.println(t.showInfo(2).Info);
        System.out.println(t.size);
        //测试
        for (int i=0;i<t.size;i++){
            System.out.println(t.showInfo(i).Info);
        }
    }
}

结果：