非线性SVM分类
尽管SVM分类器非常高效,并且在很多场景下都非常实用。但是很多数据集并不是可以线性可分的。一个处理非线性数据集的方法是增加更多的特征,例如多项式特征。在某些情况下,这样可以让数据集变成线性可分。下面我们看看下图左边那个图:
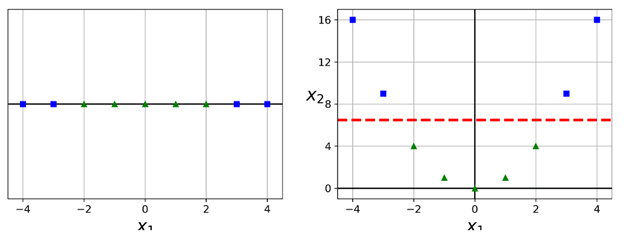
它展示了一个简单的数据集,只有一个特征x1,这个数据集一看就知道不是线性可分。但是如果我们增加一个特征x2 = (x1)2,则这个2维数据集便成为了一个完美的线性可分。
使用sk-learn实现这个功能时,我们可以创建一个Pipeline,包含一个PolynomialFeatures transformer,然后紧接着一个StandardScaler以及一个LinearSVC。下面我们使用moons数据集测试一下,这个是一个用于二元分类的数据集,数据点以交错半圆的形状分布,如下图所示:
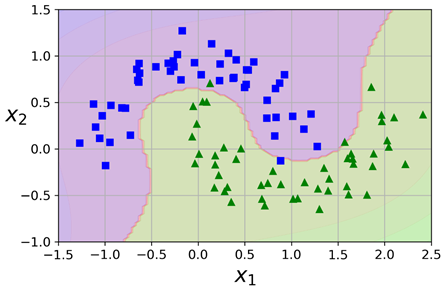
我们可以使用make_moons() 方法构造这个数据集:
%matplotlib inline import matplotlib.pyplot as plt from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42) def plot_dataset(X, y, axes): plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs") plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^") plt.axis(axes) plt.grid(True, which='both') plt.xlabel(r"$x_1$", fontsize=20) plt.ylabel(r"$x_2$", fontsize=20, rotation=0) plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) plt.show()
然后训练即可:
polynomial_svm_clf = Pipeline([ ('poly_features', PolynomialFeatures(degree=3)), ('scaler', StandardScaler()), ('svm_clf', LinearSVC(C=10, loss='hinge')) ]) polynomial_svm_clf.fit(X, y)
多项式核(Polynomial Kernel)
增加多项式特征的办法易于实现,并且非常适用于所有的机器学习算法(不仅仅是SVM)。但是如果多项式的次数较低的话,则无法处理非常复杂的数据集;而如果太高的话,会创建出非常多的特征,让模型速度变慢。
不过在使用SVM时,我们可以使用一个非常神奇的数学技巧,称为核方法(kernel trick)。它可以在不添加额外的多项式属性的情况下,实现与之一样的效果。这个方法在SVC类中实现,下面我们还是在moons 数据集上进行测试:
from sklearn.svm import SVC poly_kernel_svm_clf = Pipeline([ ('scalar', StandardScaler()), ('svm_clf', SVC(kernel='poly', degree=3, coef0=1, C=5)) ]) poly_kernel_svm_clf.fit(X, y)
上面的代码会使用一个3阶多项式核训练一个SVM分类器,如下面的左图所示:
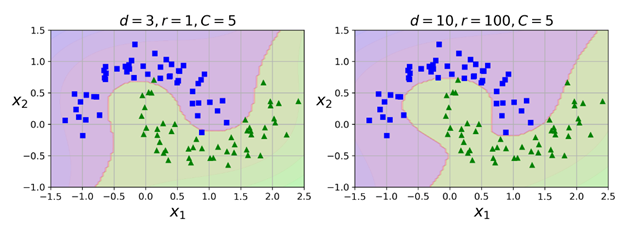
右图是另一个SVM分类器,使用的是10阶多项式核。很明显,如果模型存在过拟合的现象,则可以减少多项式的阶。反之,如果欠拟合,则可以尝试增加它的阶。超参数coef0 控制的是多项式特征如何影响模型。
一个比较常见的搜索合适的超参数的方法是使用网格搜索(grid search)。一般使用一个较大的网格搜索范围快速搜索,然后用一个更精细的网格搜索在最佳值附近再尝试。最好是能了解每个超参数是做什么,这样有助于设置超参数的搜索空间。
增加相似特征
另外一个处理非线性问题的技巧是增加一些特定的特征,这些特征由一个相似函数(similarity function)计算所得,这个相似函数衡量的是:对于每条数据,它与一个特定地标(landmark)的相似程度。举个例子,我们看一个之前讨论过的一维的数据集,给它加上两个地标(landmark)x1=-2以及x1=1(如下左图)。下面我们定义一个相似函数(similarity function),Gaussian Radial Basis Function(RBF),并指定γ = 0.3 (如下公式):
Gaussian RBF公式:
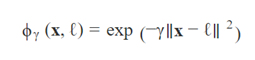
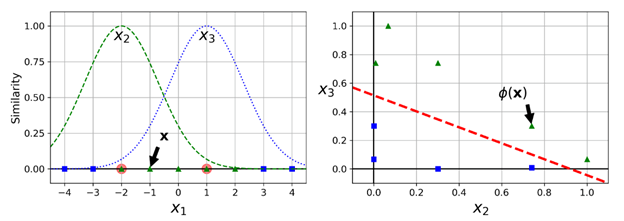
这个函数的图像是一个钟形,取值范围从0 到 1。越接近于0,离landmark越远;越接近于1,离landmark越近,等于1时就是在landmark处。现在我们可以开始计算新特征,例如,我们可以看看x1=-1的那个实例:它与第一个地标的距离是1,与第二个地标的距离是2。所以它的新特征是x2=exp(-0.3 x 12) ≈ 0.74,x3=exp(-0.3 x 22) ≈ 0.30(这里x1代表的是左图中的横坐标取值x1,x2代表的是右图中横坐标取值x2,x3代表的是右图中纵坐标取值x3)。上图中的右图显示的是转换后的数据集(剔除掉原先的特征),可以很明显地看到,现在是线性可分的。
大家可能会好奇如何选择landmark。最简单的办法是:为数据集中的每条数据的位置创建一个landmark。这个会创建出非常多的维度,并也因此可以让转换后训练集是线性可分的概率增加。缺点是,如果一个训练集有m条数据n个特征,则在转换后会有m条数据与m个特征(假设抛弃之前的特征)。如果训练集非常大的话,则会有数量非常大的特征数量。
高斯(Gaussian)RBF核
与多项式特征的方法一样,相似特征(similarity features)的方法在所有机器学习算法中都非常有用。但是它在计算所有的额外特征时,计算可能会非常昂贵,特别是在大的训练集上。不过,在SVM中,使用核方法非常好的一点是:它可以在不增加这些similarity features 的情况下,达到与增加这些特征相似的结果。下面我们使用SVC类试一下Gaussian RBF核:
rbf_kernel_svm_clf = Pipeline([ ('scalar', StandardScaler()), ('svm_clf', SVC(kernel='rbf', gamma=5, C=0.001)) ]) rbf_kernel_svm_clf.fit(X, y)
这个模型如下图中左下角的图所示:
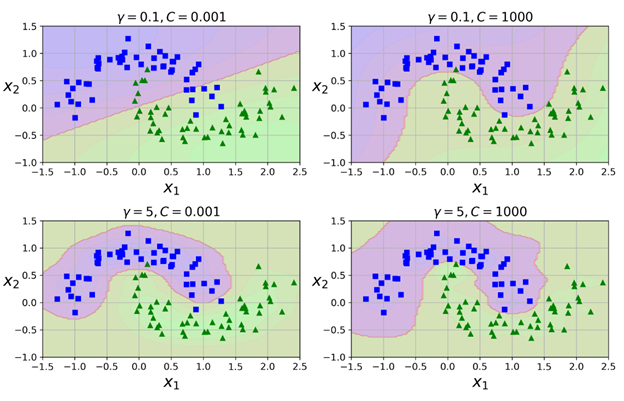
其他图代表的是使用不同的超参数 gamma(γ)与C训练出来的模型。增加gamma值可以让钟型曲线更窄(如左边上下两个图所示),并最终导致每个数据实例的影响范围更小:决策边界最终变的更不规则,更贴近各个实例。与之相反,较小的gamma值会让钟型曲线更宽,所以实例有更大的影响范围,并最终导致决策边界更平滑。所以gamma值的作用类似一个正则化超参数:如果模型有过拟合,则应该减少此值;而如果有欠拟合,则应该增加此值(与超参数c类似)。
当然也存在其他核,但是使用的非常少。例如,有些核是经常仅用于特定的数据结构。String Kernel 有时候用于分类文本文档或是DNA序列(例如,使用string subsequence kernel或者基于Levenshtein distance 的kernel)。
有这么多的核可供使用,到底如何选择使用哪个呢?根据经验,务必首先尝试线性核(linear kernel,之前提到过LinearSVC比SVC(kernel=’linear’)速度快地多),特别是训练集非常大,或者是有特别多特征的情况下。如果训练集并不是很大,我们也可以尝试Gaussian RBF kernel,它在大多数情况下否非常好用。如果我们还有充足的时间以及计算资源的话,我们也可以试验性地尝试几个其他kernel,使用交叉验证与网格搜索,特别是在有某些kernel是特别适合这个训练集的时候。
计算复杂度
LinearSVC类基于的是liblinear库,它为线性SVM实现了一个优化的算法。它并不支持核方法,但是随着训练数据与特征数目的增加,它基本是线性扩展的,它的训练时间复杂度大约是O(m x n)。
如果对模型精确度要求很高的话,算法会执行的时间更长。这个由tolerance超参数ϵ(在sk-learn中称为tol)决定。在大部分分类问题中,默认的tolerance即可。
SVC类基于的是libsvm库,它实现了一个支持核方法的算法,训练时间复杂度一般在O(m2 × n) 与 O(m3 × n) 之间。也就是说,在训练数据条目非常大时(例如几十万条),它的速度会下降到非常慢。所以这个算法特别适用于问题复杂、但是训练数据集为小型数据集或中型数据集时。不过它对特征数目的扩展良好,特别是对稀疏特征(sparse features,例如,每条数据都几乎没有非0特征)。在这种情况下,这个算法会根据大约每条数据中平均非0特征数进行扩展。下图对比了sk-learn中的SVM 分类类:

之后我们会继续介绍 SVM 回归。