“如果一个人比你年轻还比你强,那你就要被踢出去了……”——单调队列
“来来来,神犇巨佬、金牌(Au)爷、(AKer)站在最上面,蒟蒻都靠下站!!!”——优先队列
Part 1:单调队列
单调队列的功能
顾名思义,所谓单调队列,那么其中的元素从队头到队尾一定要具有单调性(单调升、单调降等)
它被广泛地用于“滑动窗口”这一类(RMQ)问题,其功能是(O(n))维护整个序列中长度为(k)的区间最大值或最小值
单调队列实现原理
滑动窗口问题
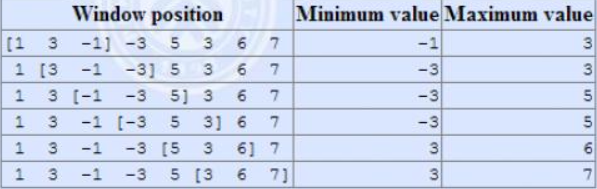
给定一个长度为(n)的序列(a)和一个窗口长度(k),窗口初始覆盖了(1 ightarrow k)这些元素
之后窗口每次向右移一个单位,即从覆盖(1 ightarrow k)变成覆盖(2 ightarrow k+1)
要求求出每次移动(包括初始时)窗口所覆盖的元素中的最大值(如图,花括号内即为被窗口覆盖的元素)
数据范围:(1leq kleq nleq 10^6,a_iin[-2^{31},2^{31}))
(Solution) (1:)暴力碾标算(O(nk))
“越接近暴力的数据结构,能维护的东西就越多”——真理
线段树和树状数组维护不了众数,但分块可以。你再看暴力,它什么都能维护……
很简单,每次从窗口最左端扫到最右端,然后取最大值就(OK)了
显然在这种数据强度下暴力是过不了的,代码就不给了
(Solution) (2:)单调队列(O(n))
思考暴力为什么慢了:因为窗口每次才移动(1)个单位,但是暴力算法每次都重复统计了(k-2)个元素
那我们把中间那一大堆数的最大值记录下来,每次进来一个元素,出去一个元素,统计一下最值,这不就快了吗?
但是,不幸的是,如果出去的那个元素正好是最值,那就得重新统计了
考虑维护一个单调不升队列,每次新元素进来之前,从这个队列的最小值向最大值依次比较
如果这个队列中的一个数(a)没有新来的那个元素(b)大,那么把(a)踢出序列
因为(a)一定在新来的数之前出现,它的值没有(b)大,所以在之后的统计中(a)永远也不可能成为最大值,就没必要记录(a)了
处理完新元素,现在看看旧元素怎么处理:
一个数(a)如果不在窗口里,那么需要把它踢出这个队列,但是如果我们每次移动都要找到这个(a)再踢出,那么复杂度又变成了(O(nk)),显然不行
发现新元素不受旧元素的影响,每次一定会进入到队列里,不会因为旧元素而把新元素卡掉,而且我们只是查询最大值,所以没有必要严格维护序列里每个值都在窗口里,只要保证最大值出自窗口里即可
因为这个队列单调不升,所以队头一定是我们要查询的最大值,那么我们可以对队头扫描,如果这个队头在窗口之外,把这个队头踢出去,新的队头是原来的第二个元素
重复上述操作,直到队头在窗口里即可,因为序列单调不升,所以队头一定是窗口内的最大值
以上就是单调队列算法的全部内容
复杂度分析
有些刚学的同学,看到循环(n)重嵌套,马上来一句:这个算法的复杂度是(O(n^n)) 的,这是不对的!!!
比如刚才我们的这个算法,看似每次窗口移动时都要对整个单调队列进行扫描,但是,从总体来看,每个元素只会入队一次,出队一次,所以复杂度是(O(n))的
核心(Code)
struct Node{
int num,und;//num是值,und是下标
Node(){}
}q[1e6+10];
int main(){
int i,head=1,tail=0;//建立单调队列维护k个数中最大值,head是队头,tail是队尾
for(i=1;i<k;i++){//先把k个元素都进来
while(head<=tial&&q[tail].num<a[i]) tail--;//如果队尾没有新元素大,那么在之后的统计中,它永远不可能成为最大值,踢出
q[++tail].und=i,q[tail].num=a[i];//新元素插入队尾
}
for(;i<=n;i++){
while(head<=tail&&q[tial].num<a[i]) tail--;
q[++tail].und=i,q[tail].num=a[i];
while(q[head].und<i-k+1) head++;//队头过时了,踢出
ans[i]=q[head].num;//统计答案
}
}
Part 2:优先队列
一个悲伤的故事背景:
从前,NOI系列比赛禁止使用(C++STL)时,优先队列是每一个(OI)选手一定会熟练手写的数据结构。
但是自从(STL)盛行,会手写优先队列的选手越来越少了……传统手艺没有人继承,真是世风日下(STL真香)啊……
优先队列的功能
优先队列有另一个名字:二叉堆
功能是维护一堆数的最大值(大根堆)/最小值(小根堆),存放在堆顶(也就是根)
注意:凡是(STL)都自带常数
优先队列实现原理
没错,实现原理就是(C++STL)
(C++STL)中(#include<queue>)头文件为我们提供了一个免费的优先队列——(priority)_(queue),但是不支持随机删除,只支持删除堆顶
优先队列的声明和操作方法
声明方法
std::priority_queue<int>Q;
上面就声明了一个(int)类型的大根堆,想要一个小根堆?没关系,你可以这么写:
std::priority_queue< int,std::vector<int>,std::greater<int> >Q;
或者把每个数入堆时都取相反数,然后在用的时候再取相反数
对于结构体,我们还有更骚的操作:重载小于号运算符
struct Node{
int x,y;
Node(){}
}
bool operator < (const Node a,const Node b){ return a.x<b.x; }
std::priority_queue<Node>Q;
这样就是按照(x)大小比较的大根堆,如果你想要小根堆,那么把重载运算符改成这句:
bool operator < (const Node a,const Node b){ return a.x>b.x; }
这样,系统就会认为小的更大,所以小的就会跑到堆顶去
但是,如你想要(int)类型的小根堆,千万不要重载运算符,这样普通的两个(int)数就不能正常比较了(系统会认为小的更大)
常用操作命令
//std priority_queue 操作命令
Q.push();//插入元素,复杂度O(logn)
Q.pop();//弹出堆顶,复杂度O(logn)
Q.size();//返回堆中元素个数,复杂度O(1)
Q.top();//返回堆顶元素,复杂度O(1)
奇技淫巧
什么?你想让(priority)_(queue)支持随机删除,但是又不想手写?(那你可真是懒
但是这能难倒人类智慧吗?显然不能,这里有一个玄学的延迟删除法,可以满足需求
我们可以维护另一个优先队列(删除堆),每次要删除一个数(假设为(x))
当需要删除(x)的时候,我们并不去真正的堆里面删除(x),而是把(x)加入删除堆
访问维护最值的堆时,看看堆顶是不是和删除堆堆顶一样,如果一样,说明这个数已经被删掉了,在原堆和删除堆中同时(pop)掉
这个方法为什么对呢?万一原堆的堆顶(x)已经被删了,而删除堆的堆顶不是(x),导致找到了错的最值,怎么办呢?
其实这种情况不可能出现。假设我们维护了一个大根堆,如果删除堆的堆顶不是(x),那必然是一个比(x)大的数(y)
如果(y)还没有被删除,那么比(y)小的(x)一定还不是堆顶,几次弹出后,堆顶是(y),发现删除堆堆顶同样是(y),(y)从原堆和删除堆中删除
换句话说,当原堆的堆顶是(x)时,删除堆堆顶和原堆中还需要删除的数一定(leq x),所以不会找到错误的最值