⼩C在研究数组的xor。
她有⼀个长度为 的数组 。
她每次会把和异或起来,然后的长度会变成
这么操作了次之后得到了长度为的数组。
她想知道在操作过程中每次的为多少?
为了避免输出过⼤,请输出第次操作后的的异或和()。
将过程图画出如下
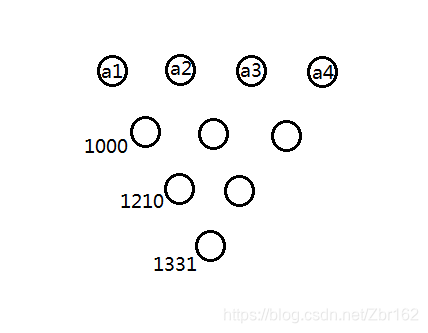
图中最左边一列的点从上向下分别表示第 此操作后的 ,
其左下角的数字表示其受数组中对应位置的异或和贡献,
发现贡献系数是符合杨辉三角的规律的, 用语言表达出来就是: ,
由于是异或操作, 当 贡献系数 是奇数的时候才会真正产生贡献 .
那么什么时候 贡献系数 为奇数呢 , 换句话说, 什么时候 为奇数呢
考虑在模的意义下使用 定理 : ,
先考虑第一项 , 当且仅当 的时候 为 ,
此时 的二进制尾部为 , 的二进制尾部为 , 由于是乘法, 这个 会导致整个式子归零 .
再考虑第二项, 对 使用 定理,
在二进制表示下相当于 与 同时去掉尾部的一个二进制位之后的一个递归过程, 回到 考虑第一项 的情况 .
于是综上所述可得:
可以枚举 , 然后在 的二进制上 “填” 得到一个可以贡献的 , 累计的贡献 .
#include<bits/stdc++.h>
#define reg register
typedef long long ll;
int read(){
char c;
int s = 0, flag = 1;
while((c=getchar()) && !isdigit(c))
if(c == '-'){ flag = -1, c = getchar(); break ; }
while(isdigit(c)) s = s*10 + c-'0', c = getchar();
return s * flag;
}
const int maxn = 8500006;
int N;
int a;
int b;
int c;
int d;
int Rd[maxn];
int sum[maxn];
ll Ans;
ll A[maxn];
void Vio(){
int cnt = 0;
for(reg int i = N; i > 1; i --){
Ans ^= A[1]*(++ cnt);
for(reg int j = 1; j < i; j ++) A[j] = A[j]^A[j+1];
}
Ans ^= A[1]*(++ cnt);
printf("%lld
", Ans);
}
void Work(){
for(reg int j = 0; j <= 22; j ++)
for(reg int i = 0; i < N; i ++)
if(!(i & (1<<j))) A[i|(1<<j)] ^= A[i];
for(reg int i = 0; i < N; i ++) Ans ^= A[i]*(i+1);
printf("%lld
", Ans);
}
int main(){
scanf("%d%d%d%d%d", &N, &a, &b, &c, &d);
A[0] = a;
for(reg int i = 1; i < N; i ++) A[i] = (A[i-1]*A[i-1] + 1ll*b*A[i-1] + c) % d;
Work();
return 0;
}