| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 2016 | Accepted: 1162 |
Description
There is a rectangular area containing n × m cells. Two cells are marked with “2”, and another two with “3”. Some cells are occupied by obstacles. You should connect the two “2”s and also the two “3”s with non-intersecting lines. Lines can run only vertically or horizontally connecting centers of cells without obstacles.
Lines cannot run on a cell with an obstacle. Only one line can run on a cell at most once. Hence, a line cannot intersect with the other line, nor with itself. Under these constraints, the total length of the two lines should be minimized. The length of a line is defined as the number of cell borders it passes. In particular, a line connecting cells sharing their border has length 1.
Fig. 1(a) shows an example setting. Fig. 1(b) shows two lines satisfying the constraints above with minimum total length 18.
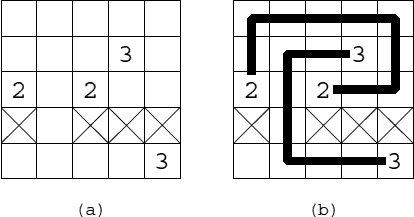
Figure 1: An example of setting and its solution
Input
The input consists of multiple datasets, each in the following format.
n m row1 … rown
n is the number of rows which satisfies 2 ≤ n ≤ 9. m is the number of columns which satisfies 2 ≤ m ≤ 9. Each rowi is a sequence of m digits separated by a space. The digits mean the following.
0:Empty
1:Occupied by an obstacle
2:Marked with “2”
3:Marked with “3”
The end of the input is indicated with a line containing two zeros separated by a space.
Output
For each dataset, one line containing the minimum total length of the two lines should be output. If there is no pair of lines satisfying the requirement, answer “0” instead. No other characters should be contained in the output.
Sample Input
5 5 0 0 0 0 0 0 0 0 3 0 2 0 2 0 0 1 0 1 1 1 0 0 0 0 3 2 3 2 2 0 0 3 3 6 5 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 2 3 0 5 9 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 3 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 9 9 0 0 0 1 0 0 0 0 0 0 2 0 1 0 0 0 0 3 0 0 0 1 0 0 0 0 2 0 0 0 1 0 0 0 0 3 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 2 0 0
Sample Output
18 2 17 12 0 52 43
题目大意:找两条不相交的路径将矩阵中的2连起来并将3连起来,求最小路径长度和-2.
分析:挺神的一道题.
用插头表示左括号右括号肯定是不够的.那表示什么呢?和bzoj2331类似,他要求什么就表示什么嘛. 令状态0表示不存在插头,状态2表示这个插头是连接2的插头,状态3表示这个插头是连接3的插头.
这样会有一个问题:如何确保一条路径2个2,2个3都经过呢?
可以在转移的时候强行规定:如果不存在插头,那么空地只能建一对状态相同的插头,标记2或者3的地方只能建一个状态与之对应的插头. 这一对和一个有啥区别? 一对表示这个点会经过两次2或3,一个表示这个点已经经过2或3了,只需要再经过一次即可.
转移要分很多类,参看:传送门.
总得来说就是讨论. 看当前所在格子是哪一类格子,由此可以得出转移到的格子有什么限制,再来讨论看看是否符合这些限制来进行转移.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 60010,inf = 0x7ffffff; int n,m,a[20][20],pow[110],ans = inf,now,pre; struct node { int head[maxn],nextt[maxn],sum[maxn],sta[maxn],tot; void clear() { memset(head,-1,sizeof(head)); tot = 0; memset(sum,127 / 3,sizeof(sum)); } void push(int x,int v) { int hashh = x % maxn; for (int i = head[hashh]; i >= 0; i = nextt[i]) { if (sta[i] == x) { sum[i] = min(sum[i],v); return; } } sum[tot] = v; sta[tot] = x; nextt[tot] = head[hashh]; head[hashh] = tot++; } }f[2]; int turnleft(int x,int pos) { return x << pow[pos]; } int get(int x,int pos) { return (x >> pow[pos]) & 3; } int del(int x,int i,int j) { return x & (~(3 << pow[i])) & (~(3 << pow[j])); } void solve2(int x,int y,int k) { int p = get(f[pre].sta[k],y - 1); int q = get(f[pre].sta[k],y); int staa = del(f[pre].sta[k],y - 1,y); int v = f[pre].sum[k]; if (staa > (1 << pow[m + 1])) return; if (a[x][y] == 1) { if (p + q == 0) { f[now].push(staa,v); return; } } else if (!p && !q) { if (a[x][y] == 0) { f[now].push(staa,v); if (a[x + 1][y] + a[x][y + 1] == 5 || a[x + 1][y] == 1 || a[x][y + 1] == 1) return; if (a[x + 1][y] == 2 || a[x][y + 1] == 2) f[now].push(staa | turnleft(2,y - 1) | turnleft(2,y),v + 1); else if (a[x + 1][y] == 3 || a[x][y + 1] == 3) f[now].push(staa | turnleft(3,y - 1) | turnleft(3,y),v + 1); else { f[now].push(staa | turnleft(2,y - 1) | turnleft(2,y),v + 1); f[now].push(staa | turnleft(3,y - 1) | turnleft(3,y),v + 1); } } else { if (a[x + 1][y] != 5 - a[x][y] && a[x + 1][y] != 1) f[now].push(staa | turnleft(a[x][y],y - 1),v + 1); if (a[x][y + 1] != 5 - a[x][y] && a[x][y + 1] != 1) f[now].push(staa | turnleft(a[x][y],y),v + 1); } } else if (p && q) { if (p + q == 5 || a[x][y] != 0) return; f[now].push(staa,v + 1); } else if (p && !q) { if (a[x][y] == 0) { if (a[x][y + 1] == 0 || a[x][y + 1] == p) f[now].push(staa | turnleft(p,y),v + 1); if (a[x + 1][y] == 0 || a[x + 1][y] == p) f[now].push(staa | turnleft(p,y - 1),v + 1); } else if (a[x][y] == p) f[now].push(staa,v + 1); } else if (!p && q) { if (a[x][y] == 0) { if (a[x][y + 1] == 0 || a[x][y + 1] == q) f[now].push(staa | turnleft(q,y),v + 1); if (a[x + 1][y] == 0 || a[x + 1][y] == q) f[now].push(staa | turnleft(q,y - 1),v + 1); } else if (a[x][y] == q) f[now].push(staa,v + 1); } } void solve() { now = 0,pre = 1; f[0].clear(); f[0].push(0,0); for (int i = 1; i <= n; i++) { pre = now; now ^= 1; f[now].clear(); for (int k = 0; k < f[pre].tot; k++) f[now].push(turnleft(f[pre].sta[k],1),f[pre].sum[k]); for (int j = 1; j <= m; j++) { pre = now; now ^= 1; f[now].clear(); for (int k = 0; k < f[pre].tot; k++) solve2(i,j,k); } } for (int i = 0; i < f[now].tot; i++) if (f[now].sta[i] == 0) ans = min(ans,f[now].sum[i]); } int main() { for (int i = 1; i <= 100; i++) pow[i] = i * 2; while (scanf("%d%d",&n,&m) == 2 && (n + m)) { ans = inf; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%d",&a[i][j]); solve(); if (ans == inf) puts("0"); else printf("%d ",ans - 2); } return 0; }