bzoj2226 [Spoj 5971] LCMSum

2226: [Spoj 5971] LCMSum

Time Limit: 20 Sec  Memory Limit: 259 MB
Submit: 1943  Solved: 849
[Submit][Status][Discuss]

Description

Given n, calculate the sum LCM(1,n) + LCM(2,n) + .. + LCM(n,n), where LCM(i,n) denotes the Least Common Multiple of the integers i and n.

Input

The first line contains T the number of test cases. Each of the next T lines contain an integer n.

Output

Output T lines, one for each test case, containing the required sum.

Sample Input

3
1
2
5

Sample Output

1
4
55

HINT

1 <= T <= 300000
1 <= n <= 1000000

分析：个人感觉比较难的一道数学题.借自GXZlegend的一张图：

　　　

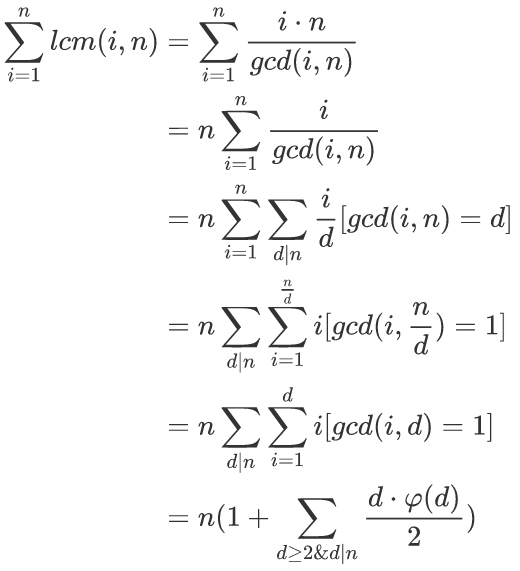
　　　　第一步转化是很显然的，gcd和lcm之间的关系嘛.

　　　　第二步是把n提出来，便于计算.

　　　　第三步为了能够对式子进行莫比乌斯反演，强行写成了两个Σ.

　　　　第四步就是关键了.在莫比乌斯反演中，gcd(x,y) == k一般都要转换成gcd(x',y') == 1. 那么gcd(i,n) == d就变成：gcd(i / d,n / d) == 1.这个i / d和外面的i / d是一样的，那么可以用i表示它们，即i的意义变成了原来的i是d的多少倍. 这时i的取值范围就和n / d有关了，所以先枚举d,然后枚举i.

　　　　第五步利用了因数是成对出现的这一条性质,这样转化便于使用欧拉函数快速求解.

　　　　第六步就是欧拉函数啦. 为什么前面有一个1呢？当d = 1时式子不一定成立,必须要特判.  后面的是一个公式：＜i并且与i互质的数的和为i * phi(i) / 2. 证明的话比较简单，如果j与i互质，那么i - j也与i互质，这样就会有phi(i) / 2对数，它们都与i互质，并且它们的和为i.

　　　　这道题还是挺难想到底的. 首先看到lcm要想到用gcd来转化. 看到gcd要想到用莫比乌斯反演. 如果用莫比乌斯反演肯定会出现2个Σ. 对gcd = k进行转化. 为了满足枚举的上下界，调换枚举顺序. 最后利用因数的成对性整体换元，套用公式即可得到答案.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
ll T,n,tot,prime[1000010],vis[1000010],phi[1000010],f[1000010];

void init()
{
    for (ll i = 2; i <= 1000000; i++)
    {
        if (!vis[i])
        {
            prime[++tot] = i;
            phi[i] = i - 1;
        }
        for (ll j = 1; j <= tot; j++)
        {
            ll t = prime[j] * i;
            if (t > 1000010)
                break;
            vis[t] = 1;
            if (i % prime[j] == 0)
            {
                phi[t] = phi[i] * prime[j];
                break;
            }
            phi[t] = phi[i] * (prime[j] - 1);
        }
    }
    for (ll i = 2; i <= 1000000; i++)
        for (ll j = i; j <= 1000000; j += i)
            f[j] += i * phi[i] / 2;
}

int main()
{
    init();
    scanf("%lld",&T);
    while (T--)
    {
        ll n;
        scanf("%lld",&n);
        printf("%lld
",(f[n] + 1) * n);
    }

    return 0;
}