bzoj4714 旋转排列

4714: 旋转排列

Time Limit: 20 Sec  Memory Limit: 512 MB
Submit: 74  Solved: 46
[Submit][Status][Discuss]

Description

Input

输入仅有一行，包含一个整数n,1≤n≤500000

Output

输出一行，包含一个整数，代表答案。

Sample Input

4

Sample Output

9
【样例解释】
k=2时的方案数为3，k=4时的方案数为6，k=1和k=3时的答案为0。
当k=2时，合法的排列有{2,1,4,3}、{3,4,1,2}和{4,3,2,1}。

分析：挺难的一道数学题.

　　　先枚举k.然后求包含长度为k的循环节的排列的数量. 直接C(n,k)是不行的，会出现下面这种情况：

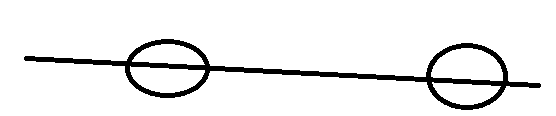，两个长度为k的循环节. C(n,k)会先把第一个循环节给算进去，然后会把第二个循环节算进去，它们就成了两种不同的方案,事实上它们是同一种方案.

　　　为什么会这样呢？因为选长度为k的循环节不仅仅要考虑到它的长度为k,还要考虑到选了多少个. 而选了多少个是不好控制的，所以我们考虑选了至少多少个，用容斥原理来算即可.

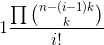　　　,枚举i表示选了多少个. 大致的原理就是：先选一个，那么就占据了k个位置，只能从剩下的n - k个位置中选k个.这是上面组合数的意义. 下面为什么要除以一个阶乘呢？因为用组合数分步计算方案数考虑了循环节的位置.

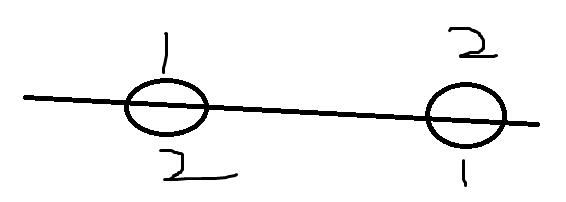,这种情况下会被算两次. 事实上它们只应该被算一次. 因为循环节的本质是一样的，我们只考虑它的个数. 所以要除以全排列数.（排列-->组合，有序-->无序）.

　　　分析完了选循环节的方案数，那么循环节里面的方案数该怎么确定呢？对于一个为k的循环节. 固定第一个元素. 那么第二个元素就只有k-1个位置可选，第三个元素只有k-2个位置可选，以此类推,方案数为(k-1)!

　　　循环节外面的方案数要怎么确定？这些数唯一的限制就是ai != i. 错位排列计算一下就好了.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll mod = 1e9+7,maxn = 500010;
ll n,ans,d[maxn],jie[maxn],ni[maxn],nijie[maxn];

ll C(ll x,ll y)
{
    return jie[x] * nijie[y] % mod * nijie[x - y] % mod;
}

int main()
{
    scanf("%lld",&n);
    d[0] = 1;
    d[1] = 0;
    d[2] = 1;
    for (ll i = 3; i <= n; i++)
        d[i] = (i - 1) * ((d[i - 1] + d[i - 2]) % mod) % mod;
    jie[1] = 1;
    ni[1] = 1;
    nijie[1] = 1;
    nijie[0] = 1;
    for (ll i = 2; i <= n; i++)
    {
        jie[i] = (jie[i - 1] * i) % mod;
        ni[i] = (mod - mod / i) * ni[mod % i] % mod;
        nijie[i] = nijie[i - 1] * ni[i] % mod;
    }
    for (ll k = 2; k <= n; k++)
    {
        ll temp = 0;
        ll res = 1;
        for (ll i = 1; i * k <= n; i++)
        {
            res = res * jie[k - 1] % mod;
            res = res * C(n - (i - 1) * k,k) % mod;
            ll tmp = res * nijie[i] % mod;
            if (i & 1)
            {
                temp += tmp * d[n - i * k] % mod;
                if (temp >= mod)
                    temp -= mod;
            }
            else
            {
                temp -= tmp * d[n - i * k] % mod;
                if (temp < 0)
                    temp += mod;
            }
        }
        ans += temp;
        if (ans >= mod)
            ans -= mod;
    }
    printf("%lld
",ans);

    return 0;
}