教材学习内容总结
Chapter16 树
非线性集合——树
- 树由一组结点及一组边构成,结点用于保存元素,边表示结点之间的连接。
- 树的根是树的最顶层中唯一的结点。
- 结点:子结点,父节点,兄弟结点,叶结点,根结点。
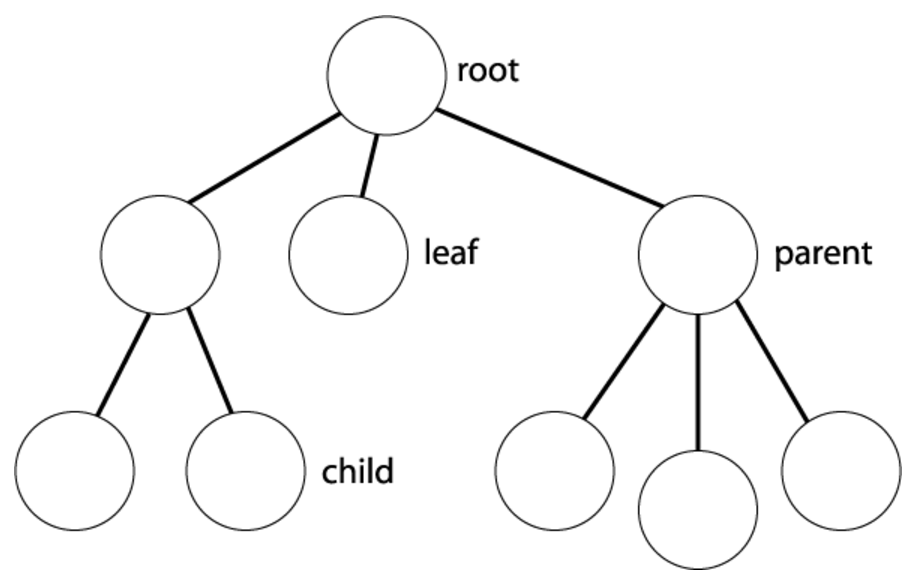
- 分类:
- 二叉树:每个结点最多有两个子结点的树。
- 完全二叉树:底层所有叶结点位于树的左侧,其余层结点全满。
- 满树:所有叶结点在同一层,每个非叶结点都正好有n个子结点。
- 平衡树:平衡因子小于等于1。
树的遍历
- 先序遍历:访问根后,从左到右遍历子树。
public void preorder(ArrayIterator<T> iter){
iter.add(element);
if(left != null)
left.preorder(iter);
if(right != null)
right.preorder(iter);
}
- 中序遍历:遍历左子树,然后访问根,之后从左到右遍历余下子树。
public void inorder(ArrayIterator<T> iter){
if(left != null)
left.inorder(iter);
iter.add(element);
if(right != null)
right.inorder(iter);
}
- 后序遍历:从左到右遍历各子树,最后访问根。
public void postorder(ArrayIterator<T> iter){
if(left != null)
left.postorder(iter);
if(right != null)
right.postorder(iter);
iter.add(element);
}
- 层序遍历:从上到下,从左到右遍历结点。
public Iterator<T> levelorder() {
LinkedQueue<BTNode<T>> queue = new LinkedQueue<>();
ArrayIterator<T> iter = new ArrayIterator<>();
if(root != null){
queue.enqueue(root);
while(!queue.isEmpty()){
BTNode<T> current = queue.dequeue();
iter.add(current.getElement());
if(current.getLeft() != null)
queue.enqueue(current.getLeft());
if(current.getRight() != null)
queue.enqueue(current.getRight());
}
}
return iter;
}
例:

如上图所示,该树的不同遍历方式依次遍历结点的顺序如下:
先序遍历:A B D H I E J M N C F G K L
中序遍历:H D I B E M J N A F C K G L
后序遍历:H I D M N J E B F K L G C A
层序遍历:A B C D E F G H I J K L M N
树的实现
- 使用数组表示树:存储在数组中位置为 n 的元素,元素的左子结点存储在(2n + 1)的位置,右子结点存储在(2 x(n+1))的位置。
- 链式结点:使用一个单独的类来定义树结点。
二叉树的实现
-
二叉树的 5 种不同形态如下图:

-
二叉树的重要性质:
若二叉树的根结点位于第1层,则- 性质1:在二叉树的第i层最多有
2^(i-1)个结点。(i≥1) - 性质2:深度为k的二叉树最多有
2^k-1个结点。(k≥1) - 性质3:对任何一棵二叉树,如果其叶结点个数为n0,度为2的结点数为n2,则有:n0=n2+1。
- 性质1:在二叉树的第i层最多有
-
特殊的二叉树:
-
满二叉树:深度为k,层数为i,根结点在第1层
结点总数2^k-1
每层结点数2^(i-1)

-
完全二叉树:树中所含的n个结点和满二叉树中编号为1至n的结点一一对应。

-
-
完全二叉树的重要性质
- 性质1:具有n个结点的完全二叉树的高度为log2(n+1)
- 性质2:如果将一棵有n个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号1, 2, …, n,则对于任意结点 i (1 ≤ i ≤ n),有:
若i=1,则该i结点是树根,它无双亲;
若2i>n,则编号为i的结点无左孩子,否则它的左孩子是编号为 2i 的结点;
若2i+1>n, 则编号为i的结点无右孩子, 否则其右孩子结点编号为2i+1;
-
二叉树的ADT及实现:
public interface BinaryTree<T> extends Iterable<T> {
// Returns the element stored in the root of the tree.
public T getRootElement();
// Returns the left subtree of the root.
public BinaryTree<T> getLeft();
// Returns the right subtree of the root.
public BinaryTree<T> getRight();
// Returns true if the binary tree contains an element that matches the specified element.
public boolean contains(T target);
// Returns a reference to the element in the tree matching the specified target.
public T find(T target);
// Returns true if the binary tree contains no elements,and false otherwise.
public boolean isEmpty();
// Returns the number of elements in this binary tree.
public int size();
// Returns the string representation of the binary tree.
public String toString();
// Returns a preorder traversal on the binary tree.
public Iterator<T> preorder();
// Returns an inorder traversal on the binary tree.
public Iterator<T> inorder();
// Returns a postorder traversal on the binary tree.
public Iterator<T> postorder();
// Performs a level-order traversal on the binary tree.
public Iterator<T> levelorder();
}
决策树
结点表示决策点(也就是进行判断的条件),左子结点表示“否”,右子结点表示“是”。
Chapter17 二叉排序树
二叉查找树
每个结点至多具有两棵子树(即在二叉树中不存在度大于2 的结点),并且子树之间有左右之分。
-
实现
- 结点定义
- 遍历方法
- 查找
- 最大值&最小值
- 前驱&后继
结点的前驱:是该结点的左子树中的最大结点。
/** * 找结点x的前驱结点:即,查找“二叉树中数据值小于该结点”的“最大结点” */ public BSTNode<T> predecessor(BSTNode<T> x){ //如果x存在左孩子,则“x的前驱结点”为“以其左孩子为根的子树的最大结点” if (x.left!=null) { return max(x.left); } /** *如果x没有左孩子,则x有以下两种可能 *1、x是“一个右孩子”,则“x的前驱结点”为“它的父结点” *2、x是“一个左孩子”,则查找“x的最低的父结点,并且该父结点要具有右孩子” *找到的这个“最低的父结点”就是“x的前驱结点” */ BSTNode<T> y=x.parent; while((y!=null)&&(x==y.left)){ x=y; y=y.parent; } return y; }结点的后继:是该结点的右子树中的最小结点。
/** * 找结点x的后继结点:即,查找“二叉树中数据值大于该结点”的“最小结点” */ public BSTNode<T> successor(BSTNode<T> x){ //如果x存在右孩子,则“x的后继结点”为“以其右孩子为根的子树的最小结点” if (x.right!=null) { return min(x.right); } /** *如果x没有右孩子,则x有以下两种可能 *1、x是“一个左孩子”,则“x的后继结点”为“它的父结点” *2、x是“一个右孩子”,则查找“x的最低的父结点,并且该父结点要具有左孩子” * 找到的这个“最低的父结点”就是“x的后继结点” */ BSTNode<T> y=x.parent; while((y!=null)&&(x==y.right)){ x=y; y=y.parent; } return y; } -
- 插入:先找到待插入的叶子结点,再在叶子结点上判断与key的关系,以判断key值应该插入到什么位置;
- 删除
- 没有左右子结点,直接删除。
删除时需要判断自己和父结点的关系,在左侧还是右侧;
如果父结点的左结点是自己,就清左侧,否则清除右侧。 - 存在左结点或者右结点,删除后需要对子结点移动。
- 同时存在左右结点,不能简单删除,但是可以通过和后继结点交换后转为前两种情况。
-
平衡树的方法:
(1)右旋(左子树长):
①使树根的左孩子元素成为新的根元素。
②使原根元素成为这个新树根的右孩子元素。
③使原树根的左孩子的右孩子,成为原树根的新的左孩子。
(2)左旋(右子树长):
①使树根的右孩子元素成为新的根元素。
②使原根元素成为这个新树根的左孩子元素。
③使原树根右孩子结点的左孩子,成为原树根的新的右孩子。
(3)右左旋(树根右孩子的左子树长):
①让树根右孩子的左孩子,绕着树根的右孩子进行一次右旋。
②让所得的树根右孩子绕着树根进行一次左旋。
(4)左右旋(树根左孩子的右子树长):
①让树根左孩子的右孩子绕着树根的左孩子进行一次左旋。
②让所得的树根左孩子绕着树根进行一次右旋。
教材学习中的问题和解决过程
- 问题1:实现遍历有哪些方式,哪一种更高效?
- 问题1解决方案:
- 传统的
for循环遍历,基于计数器的:
对于顺序存储,因为读取特定位置元素的平均时间复杂度是O(1),所以遍历整个集合的平均时间复杂度为O(n)``; 对于链式存储,因为读取特定位置元素的平均时间复杂度是O(n),所以遍历整个集合的平均时间复杂度为O(n^2)`。 - 迭代器遍历
Iterator:
对于顺序存储,没有太多意义,反而因为一些额外的操作,还会增加运行时间;
对于链式存储,因为Iterator内部维护了当前遍历的位置,所以每次遍历,读取下一个位置并不需要从集合的第一个元素开始查找,只要把指针向后移一位就行了,这样一来,遍历整个集合的时间复杂度就降低为O(n)。
soooo关于适用:
for循环遍历,基于计数器的:
顺序存储:读取性能比较高。适用于遍历顺序存储集合。
链式存储:时间复杂度太大,不适用于遍历链式存储的集合。- 迭代器遍历
Iterator:
顺序存储:如果不是太在意时间,推荐选择此方式,毕竟代码更加简洁,也防止了Off-By-One的问题。
链式存储:意义就重大了,平均时间复杂度降为O(n),还是挺诱人的,所以推荐此种遍历方式。
代码调试中的问题和解决过程
-
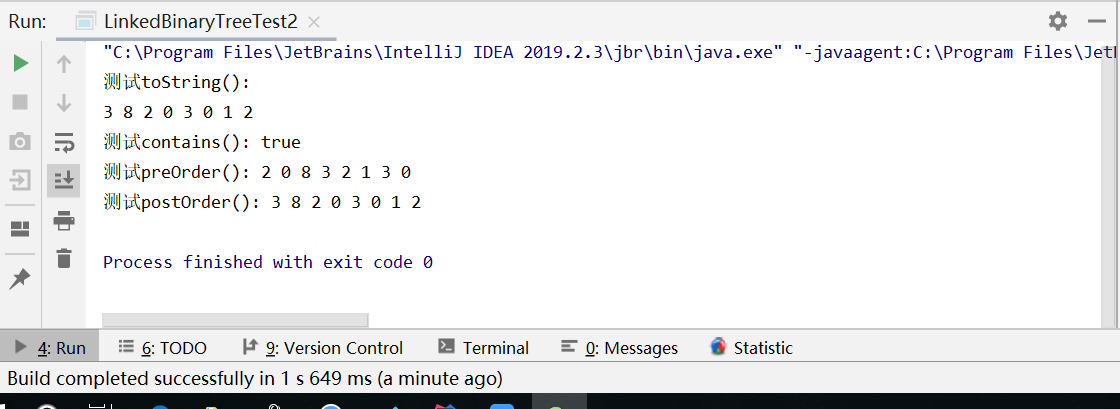
问题1:驱动程序测试toString方法时,出现空指针异常。

-
问题1解决方案:检查代码后发现自己未设root==,修改后可正常测试。
代码托管
上周考试错题总结
- It is possible to implement a stack and a queue in such a way that all operations take a constant amount of time.
A .true
B .false
正确答案: A 我的答案: B
解析: 理想情况。 - In a circular array-based implementation of a queue, the elements must all be shifted when the dequeue operation is called.
A .true
B .false
正确答案: B 你的答案: A
解析:基于循环数组的队列实现无需移动元素。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 254/254 | 2/2 | 21/21 | 开始编写简单的程序 |
| 第二周 | 132/386 | 1/3 | 26/47 | 学会使用Scanner类 |
| 第三周 | 632/1018 | 2/5 | 21/68 | 学会使用部分常用类 |
| 第四周 | 663/1681 | 2/7 | 27/95 | junit测试和编写类 |
| 第五周 | 1407/3088 | 2/9 | 30/125 | 继承以及继承相关类与关键词 |
| 第六周 | 2390/5478 | 1/10 | 25/150 | 面向对象三大属性&异常 |
| 第七周 | 1061/6539 | 2/12 | 25/175 | 算法,栈,队列,链表 |
| 第八周 | 813/7352 | 2/14 | 26/201 | 查找与排序 |
| 第九周 | 3424/10776 | 3/17 | 25/226 | 树&二叉查找树 |
-
计划学习时间:25小时
-
实际学习时间:25小时
