网络流24题-飞行员配对方案问题（1/24）

题目链接

洛谷P2756 飞行员配对方案问题

题目概述

共(n)个飞行员，分为两种，一种外籍飞行员，一种英国飞行员。其中外籍飞行员有(m)个，而英国飞行员有(n-m)个，现在告诉你每个外籍飞行员可以和哪些英国飞行员搭配开一架飞机，请你求出同时可以有多少架飞机开出，并且给出外籍飞行员于英国飞行员配对方案。

思路

因为一个飞行员不能同时上两架飞机，所以就是选出一对可以搭配的外籍飞行员和英国飞行员，然后让他们一架飞机，再去选下一对，乍一看，这不就是一个二分图的最大匹配。直接匈牙利算法，而且本身匈牙利算法也自带匹配方案。

不过我是来练习网络流的，还是网络流搞定。从网络流的方向思考，对于每个外籍飞行员和英国飞行员之间连一条边并将边的值设为(1)，然后发现没有源点和汇点，那我们就自己造一个源点和汇点。让源点都连向外籍飞行员且边权为(1)，再让英国飞行员都连向汇点边权也为(1)，这个时候建出的图的最大流就是外籍飞行员和英国飞行员的一个最大匹配。

最大流为何就是二分图的最大匹配

对于这一点，我们可以画一个图来理解一下

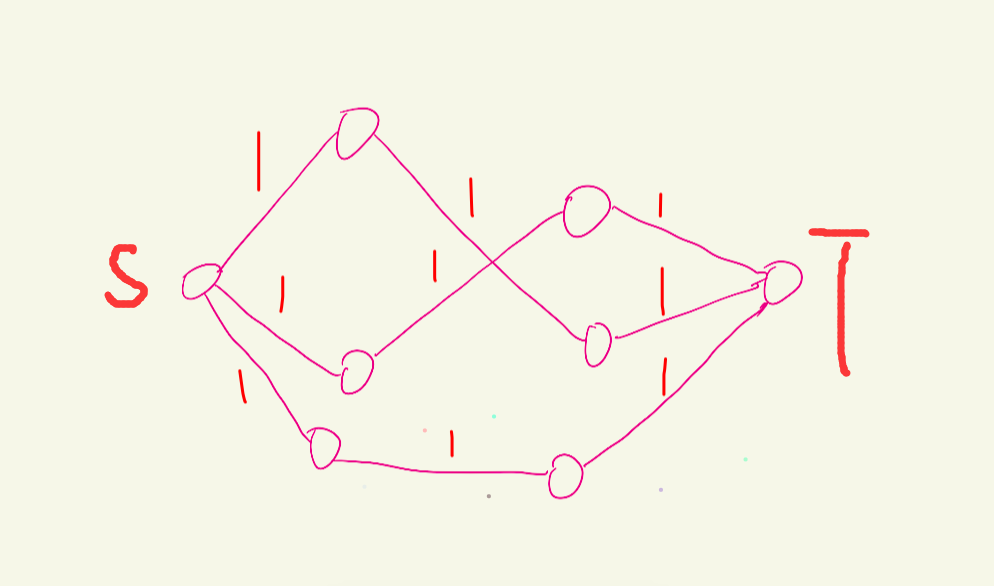
我们可以将从源点到汇点的一条增广路作为一个匹配，因为它满足从源点出发然后只经过一个外籍飞行员和一个英国飞行员，再到汇点，同时这条增广路被流过后，因为边权都为(1)，此时边权都降为0，相当于选择了这个外籍飞行员之后无法再次选择该外籍飞行员，同样的也不能从这个英国飞行员这里到汇点，即这个英国飞行员不能再选。那么我们可以把它想象成一个匹配让整个图流过了一个流量，此时我们需要求的最大匹配，就相当于转化成了同时可以最多流过多少的流量，即求该图的最大流。

如何求出方案

从上面我们可以看出，若一外籍飞行员和一英国飞行员被选为一对，那么它们之间的边权就会从(0)降为(1)，通过这一点我们就可以在求完最大流后，对外籍飞行员和英国飞行员之间的每个边进行遍历，若此时的边权为0，则该边左右两边的外籍飞行员和英国飞行员被选为一组。

#include <bits/stdc++.h>
using namespace std;

const int N = 105, M = N * N * 2;
const int INF = 1e9;

int h[N], ne[M * 2], e[M * 2], w[M * 2], idx = 0;
int t = 0;

void add(int u, int v, int we){
	e[idx] = v, ne[idx] = h[u], w[idx] = we, h[u] = idx ++ ;
}

int pre[N];
vector<pair<int,int> >v;

int d[N];

bool bfs(){
	memset(d, 0, sizeof d);
	d[0] = 1;
	queue<int> q;
	q.push({0});
	while(q.size()){
		int u = q.front();
		q.pop();
		for(int i = h[u]; ~i ; i = ne[i]){
			int to = e[i];
			if(!d[to] && w[i]){
				d[to] = d[u] + 1;
				q.push({to});
			}
		}
	}
	return d[t];
}

int dfs(int p = 0, int flow = INF){
	if(p == t){
		v.push_back({pre[pre[t]],pre[t]});
		return flow;
	}
	int tmp = flow;
	for(int i = h[p]; ~i ;i = ne[i]){
		int to = e[i];
		if(d[to] != d[p] + 1 || !w[i]) continue;
		pre[to] = p;
		int flo = dfs(to, min(w[i], tmp));
		w[i] -= flo;
		w[i ^ 1] += flo;
		tmp -= flo;
		if(tmp == 0) break;
	}
	return flow - tmp;
}

bool vis[N];

struct Node{
	int u , v;
	int id;
}node[M];
int cnt = 0;

void dinic(){
	int ans = 0;
	while(bfs()){
		ans += dfs();
	}
	cout << ans << endl;
	for(int i = 1;i <= cnt;i++){
		if(!w[node[i].id]) cout << node[i].u << " " << node[i].v << endl;
	}
}

int main(){
	memset(h, -1, sizeof h);
	int m , n;
	cin >> m >> n;
	t = n + 1;
	for(int i = 1; i <= m;i++) add(0, i, 1), add(i, 0, 0);
	for(int i = m + 1; i <= n;i++) add(i, n + 1, 1), add(n + 1, i, 0);
	while(true){
		int u, v;
		cin >> u >> v;
		if(u == -1 && v == -1) break;
		node[++ cnt] = {u, v, idx};
		add(u, v, 1);
		add(v, u, 0);
	}
	dinic();
	return 0;
}