Codeforces Round #296 (Div. 2)——A——Playing with Paper

One day Vasya was sitting on a not so interesting Maths lesson and making an origami from a rectangular a mm  ×  b mm sheet of paper (a > b). Usually the first step in making an origami is making a square piece of paper from the rectangular sheet by folding the sheet along the bisector of the right angle, and cutting the excess part.

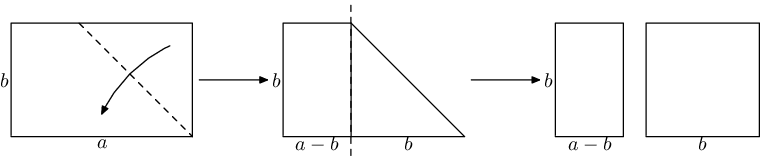
After making a paper ship from the square piece, Vasya looked on the remaining (a - b) mm  ×  b mm strip of paper. He got the idea to use this strip of paper in the same way to make an origami, and then use the remainder (if it exists) and so on. At the moment when he is left with a square piece of paper, he will make the last ship from it and stop.

Can you determine how many ships Vasya will make during the lesson?

Input

The first line of the input contains two integers a, b (1 ≤ b < a ≤ 1012) — the sizes of the original sheet of paper.

Output

Print a single integer — the number of ships that Vasya will make.

Sample test(s)

input

2 1

output

2

input

10 7

output

6

input

1000000000000 1

output

1000000000000

Note

Pictures to the first and second sample test.

大意：注意long long 要用lld输出，不过cf不能用就用cout，用d结果后面一直是零-0-好灵异

typedef long long ll;方便

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long ll;
int main()
{
    ll a,b;
    ll flag = 0;
   cin >> a >> b;
    if(a > b) ;
    else {
          ll  temp = a;
            a = b;
            b = temp;
    }
    while(a%b){
         flag += a/b;
        ll temp = b;
         b = a - (a/b)*b;
         a = temp;
    }
    flag += a/b;
   cout << flag;
}