NAND
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 65 Accepted Submission(s): 14
Problem Description
Xiaoqiang entered the “shortest code” challenge organized by some self-claimed astrologists. He was given a boolean function taking n inputs (in C++):
bool f(bool x1, bool x2, bool x3){
//your code goes here
//return something
}
All possible inputs and expected outputs of this function have been revealed:
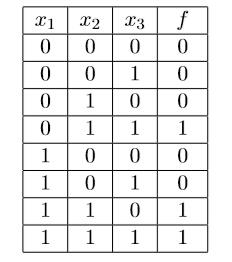
Xiaoqiang’s code must be like:
bool a = NAND(b, c);
where “a” is a newly defined variable,“b” and “c” can be a constant (0/1) or a function parameter (x1/x2/x3) or a previously defined variable. NAND is the “not-and” function:
NAND(b, c)=!(b&&c)
Because NAND is universal, Xiaoqiang knew that he could implement any boolean function he liked. Also, at the end of the code there should be a return statement:
return y;
where y can be a constant or a function parameter or a previously defined variable. After staring at the function for a while, Xiaoqiang came up with the answer:
bool a = NAND(x1, x2);
bool b = NAND(x2, x3);
bool y = NAND(a, b); return y;
Xiaoqiang wants to make sure that his solution is the shortest possible. Can you help him?
bool f(bool x1, bool x2, bool x3){
//your code goes here
//return something
}
All possible inputs and expected outputs of this function have been revealed:

Xiaoqiang’s code must be like:
bool a = NAND(b, c);
where “a” is a newly defined variable,“b” and “c” can be a constant (0/1) or a function parameter (x1/x2/x3) or a previously defined variable. NAND is the “not-and” function:
NAND(b, c)=!(b&&c)
Because NAND is universal, Xiaoqiang knew that he could implement any boolean function he liked. Also, at the end of the code there should be a return statement:
return y;
where y can be a constant or a function parameter or a previously defined variable. After staring at the function for a while, Xiaoqiang came up with the answer:
bool a = NAND(x1, x2);
bool b = NAND(x2, x3);
bool y = NAND(a, b); return y;
Xiaoqiang wants to make sure that his solution is the shortest possible. Can you help him?
Input
The first line contains an integer T (T ≤ 20) denoting the number of the test cases.
For each test case, there is one line containing 8 characters encoding the truth table of the function.
For each test case, there is one line containing 8 characters encoding the truth table of the function.
Output
For each test case, output a single line containing the minimum number of lines Xiaoqiang has to write.
Sample Input
1 00010011
Sample Output
4
题意:RT
思路:这题简化题意就是,要求构造最少的NAND式子,使得输入x1,x2,x3,输出一个8位二进制数
因为x1,x2,x3的全部组合满足0~8。那么能够将这三个数的8种值先按列压成3个8位二进制数(类似于搜索的时候开了8个栈,这样压以后仅仅需一个栈。方便处理。减枝)
x1,x2,x3的取值例如以下
000
001
010
011
100
101
110
111
按列压成8位二进制。x1 : 00001111 x2 : 00110011 x3 : 01010101
然后不难发现全部的NAND操作变成了~(a&b)
搜索的时候将新值入栈,假设搜到反复的就直接跳过,这个用一个数组记录每一个数是否存在就好了
另一个非常重要的减枝是设置一个start变量,由于每次得到新的数是从当前栈里的元素两两进行NAND操作得到的
而在DFS进入下一层的时候实际上队列中的有些元素已经两两运算过了,所以就不须要再算一次,start的含义是下一层DFS里的循环遍历应该从栈的哪个位置開始
打完表花了15秒,感觉挺快的~

版权声明:本文博客原创文章,博客,未经同意,不得转载。