A. Splits
Let's define a split of n as a nonincreasing sequence of positive integers, the sum of which is n.
For example, the following sequences are splits of 8: [4, 4], [3, 3, 2], [2, 2, 1, 1, 1, 1], [5, 2, 1].
The following sequences aren't splits of 8: [1, 7], [5, 4], [11, - 3], [1, 1, 4, 1, 1].
The weight of a split is the number of elements in the split that are equal to the first element. For example, the weight of the split [1, 1, 1, 1, 1] is 5, the weight of the split [5, 5, 3, 3, 3] is 2 and the weight of the split [9] equals 1.
For a given n, find out the number of different weights of its splits.
The first line contains one integer n (1 ≤ n ≤ 109).
Output one integer — the answer to the problem.
7
4
8
5
9
5
In the first sample, there are following possible weights of splits of 7:
Weight 1: [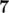 ]
]
Weight 2: [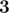 ,
, 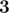 , 1]
, 1]
Weight 3: [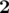 ,
, 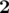 ,
, 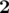 , 1]
, 1]
Weight 7: [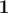 ,
, 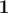 ,
, 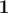 ,
, 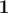 ,
, 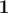 ,
, 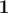 ,
, 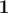 ]
]
orz,找的规律过了。
1 #pragma warning(disable:4996) 2 #include<cstdio> 3 #include<stack> 4 #include<cmath> 5 #include<string> 6 #include<cstring> 7 #include<iostream> 8 #include<algorithm> 9 using namespace std; 10 11 #define lson root<<1 12 #define rson root<<1|1 13 #define ll long long 14 15 int n; 16 17 int main() 18 { 19 while (scanf("%d", &n) != EOF) { 20 printf("%d ", n / 2 + 1); 21 } 22 return 0; 23 }
B. Messages
There are n incoming messages for Vasya. The i-th message is going to be received after ti minutes. Each message has a cost, which equals to A initially. After being received, the cost of a message decreases by B each minute (it can become negative). Vasya can read any message after receiving it at any moment of time. After reading the message, Vasya's bank account receives the current cost of this message. Initially, Vasya's bank account is at 0.
Also, each minute Vasya's bank account receives C·k, where k is the amount of received but unread messages.
Vasya's messages are very important to him, and because of that he wants to have all messages read after T minutes.
Determine the maximum amount of money Vasya's bank account can hold after T minutes.
The first line contains five integers n, A, B, C and T (1 ≤ n, A, B, C, T ≤ 1000).
The second string contains n integers ti (1 ≤ ti ≤ T).
Output one integer — the answer to the problem.
4 5 5 3 5
1 5 5 4
20
5 3 1 1 3
2 2 2 1 1
15
5 5 3 4 5
1 2 3 4 5
35
In the first sample the messages must be read immediately after receiving, Vasya receives A points for each message, n·A = 20 in total.
In the second sample the messages can be read at any integer moment.
In the third sample messages must be read at the moment T. This way Vasya has 1, 2, 3, 4 and 0 unread messages at the corresponding minutes, he gets 40 points for them. When reading messages, he receives (5 - 4·3) + (5 - 3·3) + (5 - 2·3) + (5 - 1·3) + 5 = - 5 points. This is 35 in total.
题解:读了好久的题啊,,每封信的贡献:A+(C-B)*(j-t[ i ]),这是个线性的函数讨论就好了。
感受:把t[i]写成 i ,交上去竟然过了pretest!!!!!!,强行让自己吊了一波分。
1 #pragma warning(disable:4996) 2 #include<cstdio> 3 #include<stack> 4 #include<cmath> 5 #include<string> 6 #include<cstring> 7 #include<iostream> 8 #include<algorithm> 9 using namespace std; 10 11 #define lson root<<1 12 #define rson root<<1|1 13 #define ll long long 14 15 const int maxn = 2005; 16 17 int n, A, B, C, T; 18 int t[maxn]; 19 20 int main() 21 { 22 while (cin >> n >> A >> B >> C >> T) { 23 for (int i = 1; i <= n; i++) scanf("%d", t + i); 24 int ans = 0; 25 if (C <= B) ans = A * n; 26 else for (int i = 1; i <= n; i++) ans += ((T - t[i])*(C - B) + A); 27 printf("%d ", ans); 28 } 29 return 0; 30 }