问题:
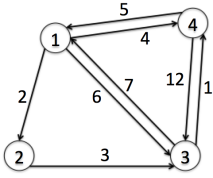
用Floyd算法求解下图各个顶点的最短距离。
解析:
任意两点间的最小距离要么直接相连,要么通过另外一个点相连。用每个点去更新两两点之间的距离即可。
设计(核心代码):
1 void floyd()
2 {
3 for (int k = 1; k <= n; ++k)
4 {
5 for (int i = 1; i <= n; ++i)
6 {
7 for (int j = 1; j <= n; ++j)
8 {
9 mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]);
10 }
11 }
12 }
13 }
分析:
O(n)遍历中间点,O(n^2)遍历两端点。
复杂度:O(n^3)
源码:
https://github.com/Big-Kelly/Algorithm

1 #include<bits/stdc++.h>
2 #include <set>
3 #include <map>
4 #include <stack>
5 #include <cmath>
6 #include <queue>
7 #include <cstdio>
8 #include <string>
9 #include <vector>
10 #include <cstring>
11 #include <iostream>
12 #include <algorithm>
13
14 #define ll long long
15 #define pll pair<ll,ll>
16 #define pii pair<int,int>
17 #define bug printf("*********
")
18 #define FIN freopen("input.txt","r",stdin);
19 #define FON freopen("output.txt","w+",stdout);
20 #define IO ios::sync_with_stdio(false),cin.tie(0)
21 #define ls root<<1
22 #define rs root<<1|1
23 #define pk push_back
24 #define Q(a) cout<<a<<endl
25
26 using namespace std;
27 const int inf = 2e9 + 7;
28 const ll Inf = 1e18 + 7;
29 const int maxn = 500 + 5;
30 const int mod = 1e9 + 7;
31 const double eps = 1e-7;
32
33 ll gcd(ll a, ll b)
34 {
35 return b ? gcd(b, a % b) : a;
36 }
37
38 ll lcm(ll a, ll b)
39 {
40 return a / gcd(a, b) * b;
41 }
42
43 ll read()
44 {
45 ll p = 0, sum = 0;
46 char ch;
47 ch = getchar();
48 while (1)
49 {
50 if (ch == '-' || (ch >= '0' && ch <= '9'))
51 break;
52 ch = getchar();
53 }
54
55 if (ch == '-')
56 {
57 p = 1;
58 ch = getchar();
59 }
60 while (ch >= '0' && ch <= '9')
61 {
62 sum = sum * 10 + ch - '0';
63 ch = getchar();
64 }
65 return p ? -sum : sum;
66 }
67
68 struct Floyd
69 {
70 int n;
71 int mp[maxn][maxn];
72
73 void init()
74 {
75 for (int i = 1; i <= n; ++i)
76 for (int j = 1; j <= n; ++j)
77 {
78 if (i == j) mp[i][j] = 0;
79 else mp[i][j] = inf;
80 }
81 }
82 void floyd()
83 {
84 for (int k = 1; k <= n; ++k)
85 {
86 for (int i = 1; i <= n; ++i)
87 {
88 for (int j = 1; j <= n; ++j)
89 {
90 mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]);
91 }
92 }
93 }
94 }
95 };
96
97 int main()
98 {
99 Floyd f;
100 int n, m;
101 scanf("%d %d", &n, &m);
102 f.n = n;
103 f.init();
104 while (m--)
105 {
106 int u, v, w;
107 scanf("%d %d %d", &u, &v, &w);
108 f.mp[u][v] = f.mp[v][u] = w;
109 }
110 f.floyd();
111 int q;
112 scanf("%d", &q);
113 while (q--)
114 {
115 int u, v;
116 scanf("%d %d", &u, &v);
117 cout << f.mp[u][v] << endl;
118 }
119 }
