关于旋转(Rotation)
很多萌新在接触计算机图形学的时候,不明白为啥要用四元数来表示旋转角度,那这篇文章主要从比较各大旋转角度,在比较中突出四元数的优点和实用。
在计算机图形学中,一个物体的位置很容易确定,直接拿到position就可以准确地定位物品的位置,但是其方向(orientation)是一个值得探讨的话题。那么通过旋转角度来可以定义两两orientation之间的改变。“朝向”是状态,“旋转”是操作。
关于旋转这个话题,接下来分成三个步骤,由浅入深地来讨论:
1,旋转矩阵
假设当前的朝向方向是 (x, y, z) 那么旋转可以由旋转矩阵得到:
沿着X轴旋转:
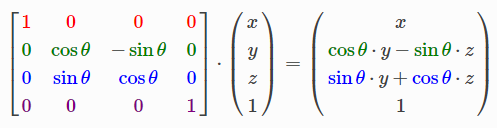
沿着y轴旋转:
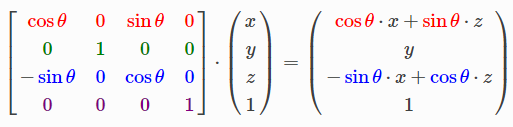
沿着z轴旋转:
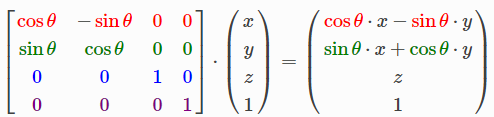
先沿着X轴转动然后在沿着Y轴转动,很可能就会导致一个问题万向节死锁问题(Gimbal Lock)
补充: 出现Gimbal Lock的本质原因在于:当第二次旋转角度为90度时,第三个轴和第一个轴转到了同个方向,因此缺少了一个自由度,导致了运动空间的限制。
取代上面方案的是沿着任意轴进行旋转特定的角度

但这种方法也是不能完全解决万向节死锁问题
2,欧拉角
针对上面的旋转问题,旋转数据量大,且存在问题,那使用欧拉角 可以使用vec3来存储一个欧拉角
Vec3 EulerAngles(RotationX, RotationY, RotationZ);
欧拉角可以分为三个部分,俯仰角:围绕x轴的pitch,偏航角:围绕y轴的yaw,滚转角:围绕z轴的roll,
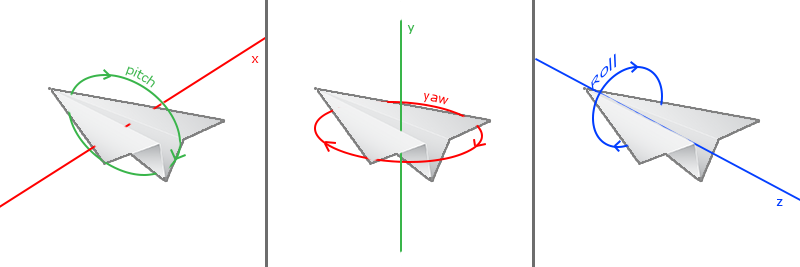
使用欧拉角可以表示任何种类的旋转角度。但是仍存在着一个欧拉角的问题:
对两个朝向进行插值比较难,简单对x,y,z简单插值得到结果不理想;
实施多次旋转很复杂且不准确,必须计算出最终的旋转矩阵,然后据此推测欧拉角
不同角度可产生同样的旋转;
针对有些操作会很复杂;如绕指定的轴旋转N角度。
3,四元数,表示旋转的好工具。
四元数是由4个数[x, y, z, w]构成,表示了如下的旋转
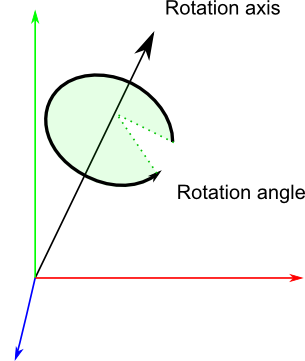
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)
其中 RotationAxis 旋转轴,RotationAngle 旋转的角度。
这样四元数中实际上存储了一个旋转轴和一个旋转角度。其中xyz分别代表了各个轴上的旋转分量。
其中[0, 0, 0, 1]表示单位四元数 (unit quaternion),表示没有旋转。
3. (1)如何从两个方向向量得到旋转角度:
r = v1 X v2 是旋转轴
O = acos(v1 * v2) 是旋转角度
然后带入上面的公式即可。
3.(2)如果先转动了q1,再转动了q2, 那么结果转动了q’ = q2 * q1。
3.(3)

四元数(quaternion)的好处是:使用角度和坐标轴的表示方法来防止了Gimbal lock的出现;避免了旋转矩阵的运算量和数据量;可以很容易的插值操作