【HDU2019多校】H

Harmonious Army

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1184    Accepted Submission(s): 414

Problem Description

Now, Bob is playing an interesting game in which he is a general of a harmonious army. There are n soldiers in this army. Each soldier should be in one of the two occupations, Mage or Warrior. There are m pairs of soldiers having combination ability. There are three kinds of combination ability. If the two soldiers in a pair are both Warriors, the army power would be increased by a. If the two soldiers in a pair are both Mages, the army power would be increased by c. Otherwise the army power would be increased by b, and b=a/4+c/3, guaranteed that 4|a and 3|c. Your task is to output the maximum power Bob can increase by arranging the soldiers' occupations.

Note that the symbol a|b means that a divides b, e.g. , 3|12 and 8|24.

 

Input

There are multiple test cases.

Each case starts with a line containing two positive integers n(n≤500) and m(m≤104).

In the following m lines, each line contains five positive integers u,v,a,b,c (1≤u,v≤n,u≠v,1≤a,c≤4×106,b=a/4+c/3), denoting soldiers u and vhave combination ability, guaranteed that the pair (u,v) would not appear more than once.

It is guaranteed that the sum of n in all test cases is no larger than 5×103, and the sum of m in all test cases is no larger than 5×104.

 

Output

For each test case, output one line containing the maximum power Bob can increase by arranging the soldiers' occupations.

 

Sample Input

3 2 1 2 8 3 3 2 3 4 3 6

 

Sample Output

12

 

SOLUTION:

这是一个。。。。。。。。论文题

 

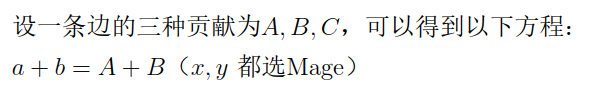
（附官方题解的图）

最后将所有的二元关系结合一下

CODE:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define MAXL 500000
#define MAX 50000
#define INF 1000000000
#define MAXN 120
#define int long long

inline int read()
{
    int x=0,t=1;char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')t=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
    return x*t;
}
struct Line
{
    int v,next,w;
}e[MAXL];
int h[MAX],cnt;
int S,T,n,m,K;
inline void Add(int u,int v,int w)
{
    e[cnt]=(Line){v,h[u],w};h[u]=cnt++;
    e[cnt]=(Line){u,h[v],0};h[v]=cnt++;
}
inline void Add2(int u,int v,int w)
{
    e[cnt]=(Line){v,h[u],w};h[u]=cnt++;
    e[cnt]=(Line){u,h[v],w};h[v]=cnt++;

}
int level[MAX];
bool BFS()
{
    memset(level,0,sizeof(level));
    level[S]=1;
    queue<int> Q;
    Q.push(S);
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        for(int i=h[u];i!=-1;i=e[i].next)
        {
            int v=e[i].v;
            if(e[i].w&&!level[v])
                level[v]=level[u]+1,Q.push(v);
        }
    }

    return level[T];
}
int DFS(int u,int flow)
{
    if(flow==0||u==T)return flow;
    int ret=0;
    for(int i=h[u];i!=-1;i=e[i].next)
    {///
        int v=e[i].v;
        if(e[i].w&&level[v]==level[u]+1)
        {
            int dd=DFS(v,min(flow,e[i].w));
            flow-=dd;ret+=dd;
            e[i].w-=dd;e[i^1].w+=dd;
        }
    }
    return ret;
}
int Dinic()
{
    int ret=0;
    while(BFS())ret+=DFS(S,INF);
    return ret;
}
int bh[MAXN][MAXN];
int g[10][MAXN][MAXN];
int aa[600];
int bb[600];

#define ll long long
signed main()
{
   while(cin>>n>>m)
   {
    memset(h,-1,sizeof(h)); cnt=0;



    S=0;T=n+1;
    ll ans=0; int l,r,a,b,c;
    for(int i=1;i<=n;i++)aa[i]=0,bb[i]=0;;

    for(int i=1;i<=m;i++)
    {

        scanf("%lld %lld %lld %lld %lld",&l,&r,&a,&b,&c);
        ans +=a+b+c;
        aa[l]+=c+b; aa[r]+=c+b;
        bb[l]+=a+b; bb[r]+=a+b;
        Add2(l,r,a+c-2*b);
    }

    for(int i=1;i<=n;i++)
    {
        Add(S,i,aa[i]);
        Add(i,T,bb[i]);
    }

  //  puts("123");

    printf("%lld
",ans-Dinic()/2);

   }
    return 0;
}