codeforces 689A A. Mike and Cellphone(水题)

题目链接：

A. Mike and Cellphone

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

While swimming at the beach, Mike has accidentally dropped his cellphone into the water. There was no worry as he bought a cheap replacement phone with an old-fashioned keyboard. The keyboard has only ten digital equal-sized keys, located in the following way:

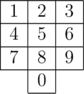
Together with his old phone, he lost all his contacts and now he can only remember the way his fingers moved when he put some number in. One can formally consider finger movements as a sequence of vectors connecting centers of keys pressed consecutively to put in a number. For example, the finger movements for number "586" are the same as finger movements for number "253":

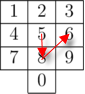
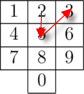
Mike has already put in a number by his "finger memory" and started calling it, so he is now worrying, can he be sure that he is calling the correct number? In other words, is there any other number, that has the same finger movements?

 

Input

 

The first line of the input contains the only integer n (1 ≤ n ≤ 9) — the number of digits in the phone number that Mike put in.

The second line contains the string consisting of n digits (characters from '0' to '9') representing the number that Mike put in.

 

Output

 

If there is no other phone number with the same finger movements and Mike can be sure he is calling the correct number, print "YES" (without quotes) in the only line.

Otherwise print "NO" (without quotes) in the first line.

 

Examples

 

input

3
586

output

NO

input

2
09

output

NO

input

9
123456789

output

YES

input

3
911

output

YES


题意;

问按下这些密码的手势顺序是否是唯一的?

思路：

由于数字很少,可以把数字的位置表示成坐标,按这个手势的顺序匹配其它的数字,看匹配后的数字还在不在这个键盘上;

AC代码：

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('
');
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e5+10;
const int maxn=1005;
const double eps=1e-10;

int check(int x,int y)
{
 if(x>=1&&x<=3&&y<=3&&y>=1)return 1;
 if(x==4&&y==2)return 1;
 return 0;
}
int fx,fy,ax,ay;
void get_pos(int num)
{
    if(num==0)fx=4,fy=2;
    else
    {
        fx=ceil(num*1.0/3);
        fy=num%3;
        if(!fy)fy+=3;
    }
}
void solve(int num)
{
      if(num==0)ax=4,ay=2;
    else
    {
        ax=ceil(num*1.0/3);
        ay=num%3;
        if(!ay)ay+=3;
    }
}
int main()
{
    int n;
    char s[14];
    read(n);
    scanf("%s",s);

    for(int i=0;i<=9;i++)
    {
        if(s[0]-'0'==i)continue;
        get_pos(i);//fx/fy;
        solve(s[0]-'0');//ax,ay;
        int flag=1;
        int tx=ax-fx,ty=ay-fy;
        for(int j=1;j<n;j++)
        {
            solve(s[j]-'0');
            if(!check(ax-tx,ay-ty))flag=0;
        }
        if(flag)
            {cout<<"NO"<<endl;return 0;}
    }
         cout<<"YES"<<endl;
        return 0;
}