个人认为其实堆排序和冒泡排序非常类似。。 简单的说就是找到数组中最大的元素并放到数组第一位,然后和最后一位交换,这样最大的元素就放到了数组最后(升序排列), 然后在从剩余的元素中再找到最大的,放到数组倒数第二位,依次操作,直到最后完全排列。
只是 他修改了 如何找到最大元素的 方法() ,那就是引入了堆的概念。
堆就是一个二叉树,他满足的条件是 节点的子节点都比自己小。
冒泡O(n2) , 堆 是 O(nlogn), 主要是差异在于 比较次数,每次交换都要重拍堆使其能够满足堆要求
为什么比较次数会变成 logn 呢。。
原因就是堆的定义: 父节点总比子节点大。 步骤如下:
1. 我们把0节点(最大) 和最后一个节点交换 (注意交换后最后的节点就不参与比较了)
2. 因为0节点发生变化,那么就要对堆进行调整使其满足堆要求。
3. 比较0 节点和其子节点(注意只有两个),我们把最大的那个和 0 交换,(这里是重点,假设子节点是A和B, 假设他们三个比较B最大,那么0 和 B 交换,那么就意味着A对应的那半边树没有变化,
那么比较次数减少一半。 只有B树发生变化,那么只去调整B相应的那半边就可以了,依次执行,实际上每一层后比较都会减半)
4. 依次执行完成调整
5. 重复上述步骤
大家画个图就能明白了,有点粗糙,凑合看吧。
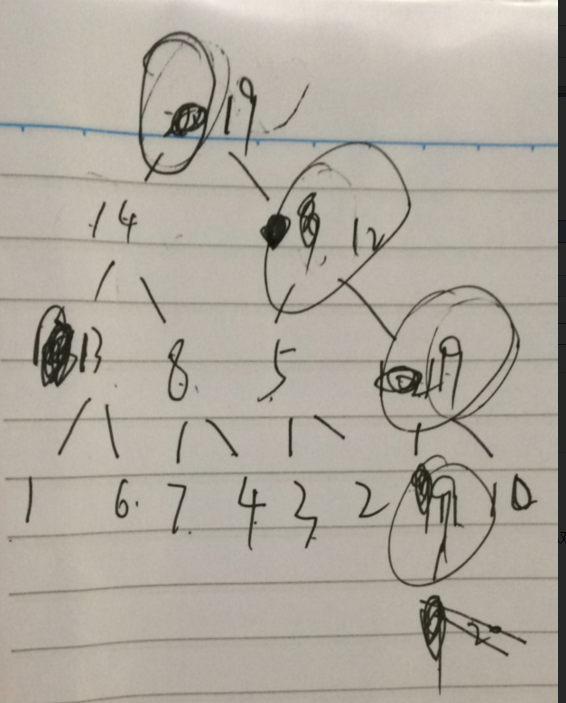
具体参看 https://www.cnblogs.com/chengxiao/p/6129630.html