参考文献
BFS的KM写法:https://blog.csdn.net/c20182030/article/details/73330556
正确性证明:算法竞赛进阶指南
DFS和BFS的写法的时间复杂度:https://www.zhihu.com/question/53200316
算法讲解
例题
讲解
转换思路
很明显,每个小人和每个房子的曼哈顿距离就是小人走到房子的代价,于是对于每个小人,向每个房子连边,边权为曼哈顿距离,那么就是求权值最小的完备匹配(每个人都有房子的匹配)。
KM算法讲解
事实上KM求的是最大权匹配
取个负不就行了
下文的证明默认是求最大权匹配,且边权都是整数(当然,后面会讲小数做法)。
事实上,如果没有的边会默认边权为(-∞)
交错树
以下摘自算法进阶(因为这种专业术语我是真的不会啊)。
在匈牙利算法的(DFS)中,如果从某个左部借点出发寻找匹配失败,那么所有访问过的节点,以及为了访问这些节点而经过的边,共同构成的一棵树。
这棵树的根是一个左部节点,所有叶子节点也都是左部节点(因为最终匹配失败了),并且树上第(1,3,5,...)层都是非匹配边,第(2,4,6...)层的边都是匹配边。因此,这棵树被称为交错树。
顶标
全称“顶点标记点”。
在图中,我们会给每个点一个权值,但是在初始化的时候,左边的点和右边的点是不一样的(左边的点集为(|X|),右边的点集为(|Y|)),右边的点权一开始为(0),而右边的点(x_i)的初始化为(max(w(x_{i},y_{j}))),其中(w)表示边权,(y_{j}∈Y)。
相等子图
二分图的所有节点,以及满足(d_{x_{i}}+d_{y_{j}}=w(x_{i},y_{j}))的边所构成的子图叫相等子图。
过程
首先,在相等图上跑匈牙利算法。
假如目前是(dfs(x_{i})),如果没有找到增广路,说明相等子图不够大,那么对于访问过的(x_{i})和(y_{j}),(d_{x_{i}}--,d_{y_{j}}++)。
然后再跑匈牙利,反复如此,知道(x_{i})找到增广路。
那么,为什么这样子干,最终一定会找到增广路呢?
如果(x_{i},y_{j})都被访问过了,那么(x_{i}+y_{j})并不会变,所以((x_{i},y_{j}))这条边是否在子图中并没有变化。
但是如果(x_{i})访问过,(y_{j})没有被访问过,那么(x_{i}+y_{j})会比原来小(1),有可能被加入到子图中,这样每次顶标的修改,就意味着相等子图可能在扩大,实际上,如果这条边加入进去,则意味着能多访问到一个点了。
但是如果(y_{j})被访问过了,而(x_{i})没有被访问,那么(x_{i}+y_{j})会比原来大(1),直接被删除出去,但是这条边只有在(x_{i})要访问(y_{j})才会用到,但是(y_{j})我原本就能访问到,还需要这条边干嘛?所以不会导致能访问到的点减少。
所以修改顶标只会导致能访问到的点增加,所以最后一定能匹配上。
最后全部匹配完了,答案就是顶标之和。
事实上,改变顶标还有一个性质,因为左边的点除了(DFS)进入的点,都是通过匹配边到达的,而右边的点被访问之后,因为不存在增广路,则一定会有匹配边,便一定会访问一个没有被访问过的左部点,所以左部点的个数是右部点个数(+1),所以这样修改会使顶标之和(-1)。
正确性证明
首先,完备匹配的权值和一定小于等于顶标之和。
我们先证明(x_{i}+y_{j}≥w(x_{i},y_{j})),刚开始的初始化肯定满足,且如果这条边被加入了相等子图之后,(x_{i})被访问,(y_{j})一定也会被访问到,所以(x_{i}+y_{j})不变,而(y_{j})单独被访问,则(x_{i}+y_{j})只会增加,也不会小于(w(x_{i},y_{j}))(还会被踢出相等子图),如果不在相等子图,减一最多从('>')变成('='),然后加入相等子图,如果还是('>'),那也还是大于等于(w(x_{i},y_{j})),得证。(简单来说就是上述过程一定一直满足(x_{i}+y_{j}≥w(x_{i},y_{j})))
根据上述结论,每种完备匹配的匹配边权值和小于等于顶标之和。
而在找到完备匹配方案时,这种方案恰好等于顶标之和,又根据方案都小于等于顶标之和,所以这种方案是最大权的,等于现在的顶标之和。
事实上用此方法应该可能可以证明用此方法也可以做(n)个人,(m)个房子,每个人都要有个房子的最大权匹配。也许
优化
我们发现,这种方法是在是太慢了,尤其是当边权很大的时候,时间简直太慢了,我们称其为(1)号做法,而且这种做法还很难处理小数(难道小数用(1e-4)什么的?)。
我们发现,有时候(+1,-1)还不一定有边会加入子图当中,因为(min(d_{x_{i}}+d_{y_{j}}-w(x_{i},y_{j})))可能(>1),因此可以直接用(slack)存储不在相等子图的边的(d_{x_{i}}+d_{y_{j}}-w(x_{i},y_{j})),顶标一次(+slack)和(-slack),那么每次加减都可以让一条边加入到相等子图中。
且这样子做,小数边权的问题也就迎刃而解了,因为(slack)也可以是小数吗。
我们称其为(2)号做法。
以下代码的边权就是小数的。
double vwh[N],vbl[N],slack;//边权
int match[N];
bool st1[N],st2[N];
bool check(int x)
{
st1[x]=1;
for(int k=last[x];k;k=a[k].next)//实际上n^2直接用邻接矩阵即可
{
int y=a[k].y;
if(st2[y])continue;
if(vwh[x]+vbl[y]-a[k].c>1e-4)slack=mymin(slack,(vwh[x]+vbl[y])-a[k].c);
else
{
if(!match[y]){match[y]=x;return 1;}
else if(!st1[match[y]])
{
st2[y]=1;
if(check(match[y])==1){match[y]=x;return 1;}
}
}
}
return 0;
}
int main()
for(int i=1;i<=n;i++)
{
while(1)
{
slack=999999999.0;
memset(st1,0,sizeof(st1));memset(st2,0,sizeof(st2));
if(check(i)==1)break;
for(int j=1;j<=n;j++)
{
if(st1[j])vwh[j]-=slack;
if(st2[j])vbl[j]+=slack;
}
}
}
但是,这种做法并不是最快的。
因为我们发现,(slack)如果在(DFS)中判断,加入的边的两个顶点可能都是被访问的点,所以这条边加入进去也不会增加能被访问点的个数(换而言之这条边很废)
因此,考虑(DFS)后再外面找(slack),只找左边被访问过,右边没被访问过的边。
我们称其为(3)号做法。
double ma[N][N];//邻接矩阵
double vwh[N],vbl[N],slack;//让白点找黑点
int match[N],n;
bool st1[N],st2[N];
bool check(int x)
{
st1[x]=1;
for(int y=1;y<=n;y++)
{
if(st2[y])continue;
if(vwh[x]+vbl[y]-ma[x][y]<=1e-4)
{
if(!match[y]){match[y]=x;return 1;}
else if(!st1[match[y]])
{
st2[y]=1;
if(check(match[y])==1){match[y]=x;return 1;}
}
}
}
return 0;
}
int main()
for(int i=1;i<=n;i++)
{
while(1)
{
slack=999999999.0;
memset(st1,0,sizeof(st1));memset(st2,0,sizeof(st2));
if(check(i)==1)break;
for(int j=1;j<=n;j++)
{
if(st1[j])
{
for(int k=1;k<=n;k++)if(!st2[k])slack=mymin((vwh[j]+vbl[k])-ma[j][k],slack);
}
}
for(int j=1;j<=n;j++)
{
if(st1[j])vwh[j]-=slack;
if(st2[j])vbl[j]+=slack;
}
}
}
但是,这样还不是最优秀的,因为我们发现,每一次跑完(DFS)并修改顶标,能访问到的点集不会缩小,只会扩大,且原本就在点集中的元素不会消失,所以并不用每次(DFS)都去跑一遍,可以用(BFS)代替修改顶标扩展子图的过程。
此代码中的(slack)是个数组,表示如果下一次要把这个点加入进去,(slack)要等于多少(在下文代码中,真正的(slack)是(d)变量)
我们称其为(4)号做法。
int pre[N],match[N];
double slack[N],val[N][N],d1[N],d2[N];
bool v[N];//判断右边的点是否被访问过
void bfs(int st)
{
double d;
for(int i=1;i<=n;i++)slack[i]=999999999.0,v[i]=0;//初始化
match[0]=st;//为了方便后面的while设置的
int py=0,px,yy;
while(match[py]!=0)//如果现在找到的右边的点没有配偶,那么找到增广路
{
px=match[py];v[py]=1;
d=999999999.0;
for(int i=1;i<=n;i++)
{
if(!v[i])
{
if(slack[i]>d1[px]+d2[i]-val[px][i])slack[i]=d1[px]+d2[i]-val[px][i],pre[i]=py;//更新这个点的slack
if(slack[i]<d)d=slack[i],yy=i;//判断下一个要加入的点是谁
}
}
for(int i=0/*注意这个地方为0*/;i<=n;i++)
{
if(v[i])d1[match[i]]-=d,d2[i]+=d;
else slack[i]-=d;//边权被改动了,所以slack[i]-=d
}
py=yy;
}
while(py)match[py]=match[pre[py]],py=pre[py];//匹配
}
void KM()
{
for(int i=1;i<=n;i++)bfs(i);//对每个左边的点都这么干
}
但实际上,在最后一道练习题我才用了这个实现方式,其他的都是用3号做法的。
接下来分析没种做法的时间复杂度问题。
(1)号做法,理论上等于(找一个点的对象时扩展(n)个点的顶标变化量(×n^3)),但是由于顶标改动会给后面带来影响(后面找对象更少的改动顶标),而且这种本质上也不是定值,以及一些更加神奇的事情,分析难度很大(因为我原本就不是很会分析时间复杂度,只是乱搞罢了),但是其实还有一种比这个更加准确一点应该的时间复杂度,为(O((开始顶标和-答案)n^2))。(这个我是真的不会。。。)
(2)号做法,每次修改顶标一定会导致一条边加入到相等子图中,所以是(O(mn^2))((n^2)是匈牙利的时间),但是发现可能在这次(DFS)中,会把一些边从相等子图删除,但是每条边对于一个点只会删除一次,加入一次,所以应该是(O(mn^3))的,也就是(O(n^5))的。但是他们都说是n^4的,果然是我错了吗
(3)号做法,由于每次修改顶标一定会有一个点加入进来,所以为(O(n*n*n^2)=O(n^4))。
(4)号做法,每次修改顶标只会有一个点加入进来,加入进来只会跑其的(n)条边,所以是(O(n*n*n)=O(n^3))的。(实际上就是把(3)号做法(n)次修改顶标重复跑的部分合成了一次跑),正好对应了(KM)的时间复杂度是(O(n^3))的。
所以,(KM)算法本质是(O(n^3))的,和匈牙利一个样子,真的是优美的算法啊。
代码真的是很神奇的东西,稍微加上一点优化,就少了一个(n)。当然也有可能是我分析错了。
代码
本代码采用(3)号做法。
#include<cstdio>
#include<cstring>
#include<cmath>
#define N 110
#define M 11000
using namespace std;
template<class T>
inline T mymin(T x,T y){return x<y?x:y;}
template<class T>
inline T mymax(T x,T y){return x>y?x:y;}
template<class T>
inline T zabs(T x){return x<0?-x:x;}
struct ZUOBIAO
{
int x,y;
}a1[N],a2[N];
inline double dis(ZUOBIAO x,ZUOBIAO y){return zabs(x.x-y.x)+zabs(x.y-y.y);}
int n,m,n1,n2;
char st[N];
int ma[N][N];
bool st1[N],st2[N];
int match[N];
int slack,d1[N],d2[N];
bool dfs(int x)
{
st1[x]=1;
for(int i=1;i<=n1;i++)
{
if(!st2[i] && d1[x]+d2[i]==ma[x][i])
{
st2[i]=1;
if(!match[i] || dfs(match[i])==1){match[i]=x;return 1;}
}
}
return 0;
}
int KM()
{
for(int i=1;i<=n1;i++)
{
d1[i]=-999999999;d2[i]=0;match[i]=0;
for(int j=1;j<=n1;j++)
{
ma[i][j]=-dis(a1[i],a2[j]);//取负号,找最大
d1[i]=mymax(d1[i],ma[i][j]);
}
}
for(int t=1;t<=n1;t++)
{
while(1)
{
slack=999999999;
memset(st1,0,sizeof(st1));
memset(st2,0,sizeof(st2));
if(dfs(t)==1)break;
for(int i=1;i<=n1;i++)
{
if(!st1[i])continue;
for(int j=1;j<=n1;j++)
{
if(!st2[j])slack=mymin(slack,d1[i]+d2[j]-ma[i][j]);
}
}
for(int i=1;i<=n1;i++)if(st1[i])d1[i]-=slack;
for(int i=1;i<=n1;i++)if(st2[i])d2[i]+=slack;
}
}
int ans=0;
for(int i=1;i<=n1;i++)ans+=d1[i]+d2[i];//顶标之和就是答案
return -ans;
}
int main()
{
while(1)
{
n1=n2=0;
scanf("%d%d",&n,&m);
if(!n)break;
for(int i=1;i<=n;i++)
{
scanf("%s",st+1);
for(int j=1;j<=m;j++)
{
if(st[j]=='H')a2[++n2].x=i,a2[n2].y=j;
else if(st[j]=='m')a1[++n1].x=i,a1[n1].y=j;
}
}
printf("%d
",KM());
}
return 0;
}
练习
蚂蚁
这道题目是很巧妙的证明加上套模板。
考虑黑边点匹配的边权为他们的距离,权值和最小的匹配方案就是没有交点的方案。
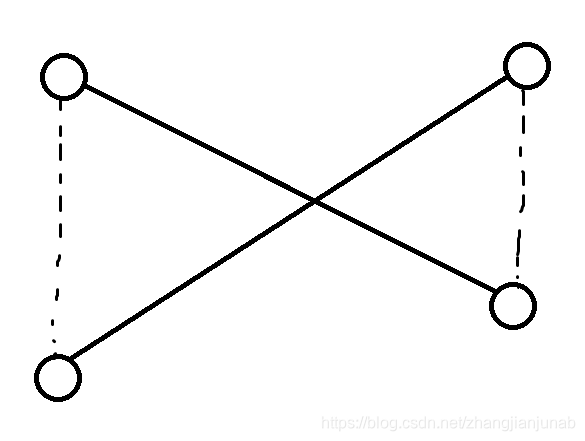
如果有交点,也就是上图直线方案,换成虚线方案距离和一定会变小,根据三角形两边之和大于第三边就可以证明了。
由于方案的距离和不可能无限变小,因为方案总数也就(n!),最终会变成没有交点的方案,证毕。
然后建模跑模板即可,本题仍然使用(3)号做法。
#include<cstdio>
#include<cstring>
#include<cmath>
#define N 110
#define M 11000
using namespace std;
template<class T>
inline T mymin(T x,T y){return x<y?x:y;}
template<class T>
inline T mymax(T x,T y){return x>y?x:y;}
struct DIAN
{
int x,y;
}bl[N],wh[N];
inline double dis(DIAN x,DIAN y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}
double ma[N][N];
double vwh[N],vbl[N],slack;//让白点找黑点
int match[N],n;
bool st1[N],st2[N];
bool check(int x)
{
st1[x]=1;
for(int y=1;y<=n;y++)
{
if(st2[y])continue;
if(vwh[x]+vbl[y]-ma[x][y]<=1e-4)
{
if(!match[y]){match[y]=x;return 1;}
else if(!st1[match[y]])
{
st2[y]=1;
if(check(match[y])==1){match[y]=x;return 1;}
}
}
}
return 0;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d%d",&bl[i].x,&bl[i].y);
for(int i=1;i<=n;i++)scanf("%d%d",&wh[i].x,&wh[i].y);
for(int i=1;i<=n;i++)
{
vwh[i]=-999999999.0;
for(int j=1;j<=n;j++)
{
ma[i][j]=-dis(wh[i],bl[j]);
vwh[i]=mymax(vwh[i],ma[i][j]);
}
}
for(int i=1;i<=n;i++)
{
while(1)
{
slack=999999999.0;
memset(st1,0,sizeof(st1));memset(st2,0,sizeof(st2));
if(check(i)==1)break;
for(int j=1;j<=n;j++)
{
if(st1[j])
{
for(int k=1;k<=n;k++)if(!st2[k])slack=mymin((vwh[j]+vbl[k])-ma[j][k],slack);
}
}
for(int j=1;j<=n;j++)
{
if(st1[j])vwh[j]-=slack;
if(st2[j])vbl[j]+=slack;
}
}
}
for(int i=1;i<=n;i++)printf("%d
",match[i]);
return 0;
}
[SDOI2018]新生舞会
很明显的(01)分数规划+KM算法。
这道题目放在最后只是单纯的因为我打的是(n^3)打法。只是单纯的因为我是第二快
#include<cstdio>
#include<cstring>
#define N 110
using namespace std;
//都是n^2的了,用什么边目录啊,正经人谁用边目录啊。
template<class T>
inline T mymax(T x,T y){return x>y?x:y;}
int n;
int pre[N],match[N];
double slack[N],val[N][N],d1[N],d2[N];
bool v[N];
void bfs(int st)
{
double d;
for(int i=1;i<=n;i++)slack[i]=999999999.0,v[i]=0;
match[0]=st;
int py=0,px,yy;
while(match[py]!=0)
{
px=match[py];v[py]=1;
d=999999999.0;
for(int i=1;i<=n;i++)
{
if(!v[i])
{
if(slack[i]>d1[px]+d2[i]-val[px][i])slack[i]=d1[px]+d2[i]-val[px][i],pre[i]=py;
if(slack[i]<d)d=slack[i],yy=i;
}
}
for(int i=0;i<=n;i++)
{
if(v[i])d1[match[i]]-=d,d2[i]+=d;
else slack[i]-=d;
}
py=yy;
}
while(py)match[py]=match[pre[py]],py=pre[py];
}
int a[N][N],b[N][N];
bool pd(double shit)
{
for(int i=1;i<=n;i++)
{
d2[i]=0;d1[i]=-999999999.0;match[i]=0;
for(int j=1;j<=n;j++)val[i][j]=a[i][j]-shit*b[i][j],d1[i]=mymax(val[i][j],d1[i]);
}
for(int i=1;i<=n;i++)bfs(i);
double ans=0;
for(int i=1;i<=n;i++)ans+=d1[i]+d2[i];
return ans>=0;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)scanf("%d",&a[i][j]);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)scanf("%d",&b[i][j]);
}
double l=0,r=10000,mid,ans=0;
while(r-l>=1e-9)
{
mid=(l+r)/2;
if(pd(mid)==1)ans=mid,l=mid;
else r=mid;
}
printf("%.6lf
",ans);
return 0;
}
竟然还比费用流跑得快。
事实上我也不知道费用流时间复杂度是多少。
最快的貌似也是BFS KM
小结
但是实际上(KM)只能处理完备匹配,万能还是费用流啊。